
- •Раздел 1. Основы расчета строительных конструкций
- •Равномерно распределенные временные нагрузки на перекрытия зданий
- •Раздел 2. Металлические конструкции
- •Раздел 3. Конструкции из дерева и пластических масс
- •Раздел 4. Каменные и армокаменные конструкции.
- •Толщина защитного слоя цементного раствора для армокаменных конструкций
- •Раздел 5. Железобетонные конструкции.
- •1. Сущность железобетона
- •2. Предварительно напряженные железобетонные конструкции
- •Ориентировочное сравнение свойств обычных железобетонных и предварительно напряженных конструкций
- •3. Технологические особенности изготовления железобетонных конструкций
- •1. Общие сведения
- •2. Классификация предварительно напряженных конструкций
- •3. Методы и способы создания предварительного напряжения в конструкциях
- •Монолитные перекрытия, конструктивные схемы, особенности расчета
- •Ребристые перекрытия с плитами, опертыми по контуру
- •Сборно-монолитные перекрытия
- •Раздел 6. Основания и фундаменты.
Толщина защитного слоя цементного раствора для армокаменных конструкций
Вид армированной конструкции |
Защитный слой мм, для конструкций, расположенных |
||
В помещениях с нормальной влажностью |
На открытом воздухе |
Во влажных и мокрых помещениях, а также в резервуарах, фундаментах и т. п. |
|
Балки и столбы Стены |
20 10 |
25 15 |
30 20 |
При определении коэффициента продольного изгиба ф по табл. 1 значение упругой характеристики а принимается по табл. 18 приложения III, как для неармированной кладки.
При расчете внецентренно-сжатых элементов различают два случая:
а) случай больших эксцентриситетов, когда соблюдаются условия:
при любой форме сечения: Sc<0,8S0
при прямоугольной форме сечения: x<0,55h0
б) случай малых эксцентриситетов, когда указанные условия не соблюдаются.
S0 – статический момент всего сечения кладки относительно центра тяжести растянутой или менее сжатой арматуры Aa, определяемой по формуле:
при любой форме сечения: S0=A(h0-y),
при прямоугольной
форме сечения: S0=0,5b
Sc – статический момент сжатой зоны сечения относительно центра тяжести той же арматуры, определяется по формулам таблицы 2.
Следует отметить, что при наличии продольной арматуры в сжатой зоне для обеспечения полного использования этой арматуры должно быть соблюдено условие:
при любой форме сечения: z≤h0-a’
при прямоугольной форме сечения: x≥2a’ – это условие следует соблюдать лишь при больших эксцентриситетах.
Таблица 2
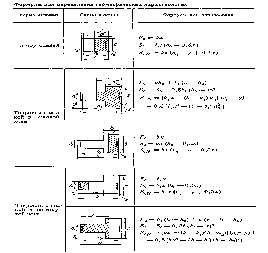

Рис. 3. Расчетная схема при внецентренном сжатии каменной кладки с продольной арматурой:
а — случай больших эксцентриситетов; б — случай малых эксцентриситетов.
Случай больших эксцентриситетов (рис. 3, а). Сумма моментов всех сил относительно точки приложения равнодействующей усилий в растянутой арматуре:
N·e≤φ1·mg1·(0,85·ω·R·Sc+Ra·Àa·Za)
сумма проекций всех сил на продольную ось элемента:
N≤ φ1·mg1·(0,85·ω·R·Ac+Ra·Àa - Ra Aa)
положение нейтральной оси определяется из уравнения моментов относительно точки приложения внешней нагрузки
0,85·ωR·ScN± Ra·Àa·é–Ra·Aa·e=0
Знак «плюс» в этой формуле принимается при расположении продольной силы N за пределами промежутка между центрами тяжести арматур Aa и Àa, знак «минус» — при расположении N в пределах этого промежутка.
При отсутствии продольной арматуры в сжатой зоне сечения в формулах нужно принять Àa = 0, а коэффициент 0,85 заменить единицей. Тогда эти формулы примут вид соответственно:
N·e≤φ1·mg1·ω·R·Sc
N≤ φ1·mg1·(0,85·ω·R·Ac+Ra·Aa)
ωR·ScN–Ra·Aa·e=0
Случай малых эксцентриситетов (рис. 3, б). Сумма моментов всех сил относительно точки приложения равнодействующей усилий в менее сжатой арматуре:
N·e≤φ1·mg1·(0,85·ω·R·Sc+Ra·Àa·za)
в более сжатой арматуре:
N·é ≤φ1·mg1·(0,85·ω·R·Sc+Ra·Aa·za)
При одиночном армировании эти условия примут вид:
N·e≤φ1·mg1·ω·R·Sc
N·é ≤φ1·mg1·ω·R·Sc
В формулах величины Sc и Sc представляют собой значение статических моментов сжатой зоны сечения относительно соответствующих точек, при которых элемент работает в граничных условиях между случаями больших и малых эксцентриситетов, т. е.
Sc = 0,8S0
Sc = 0,85 S0
Здесь So - статический момент всего сечения кладки относительно центра тяжести сжатой арматуры Àa, определяемый по формуле:
при любой форме сечения
S'0 = A(y-a')
при прямоугольной форме сечения
S'0 = 0,5bh0
Входящие в формулы величины площади сжатой зоны кладки Ac и статического момента этой зоны относительно точки приложения равнодействующей усилий в растянутой арматуре Sc и продольной силы Scn приведены в табл. 8.
Для прямоугольных сечений формулы после подстановки в них значений Ac, Sc и Scn из табл. 8 примут вид соответственно:
для случая больших эксцентриситетов:
при двойном армировании
N·e≤φ1·mg1·(0,85·ω·R·bx(h0-0,5x)+Ra·Àa·za)
N≤ φ1·mg1·(0,85·ω·R·bx+ Ra·Àa-Ra·Aa)
0,85·ωR·bx(e-h0-0,5x)± Ra·Àa·é–Ra·Aa·e=0
при одиночном армировании
N·e≤φ1·mg1·ω·R·bx(h0-0,5x)
N≤ φ1·mg1·(ω·R·bx-Ra·Aa)
ωR·bx(e-h0-0,5x)–Ra·Aa·e=0
для случая малых эксцентриситетов: при двойном армировании
N·e≤φ1·mg1·(0,34·ω·R·bh0+Ra·Àa·za)
N·é≤ φ1·mg1·(0,34·ω·R·bh0+ Ra·Aa·za)
при одиночном армировании
N≤0,4· φ1·mg1· R·bh0
При проектировании элементов с продольной арматурой встречается два типа задач.
4.4. Основные положения проектирования каменных конструкций.
1. Здание представляет собой пространственную систему из отдельных элементов, связанных между собой. Наличие связей между этими элементами обусловливает их совместную работу на вертикальные и горизонтальные нагрузки. Обеспечение связей примыкающих или пересекающихся стен между собой осуществляется перевязкой камней (иногда армированием), а перекрытий и покрытий со стенами — анкерами.
На характер восприятия вертикальных нагрузок эти связи существенного влияния не оказывают (кроме повышенной устойчивости). В восприятии горизонтальных нагрузок наличие поперечных конструкций (опор) и расстояние между ними имеет определяющее значение. По степени жесткости горизонтальные опоры делятся на жесткие и упругие.
Жесткие опоры: поперечные устойчивые конструкции — поперечные каменные и бетонные стены толщиной не менее 12 см, железобетонные стены толщиной не менее 6 см, контрфорсы, поперечные рамы с жесткими узлами, отрезки поперечных стен и другие конструкции, рассчитанные на горизонтальные нагрузки; покрытия и междуэтажные перекрытия при расстояниях между поперечными устойчивыми конструкциями не более указанных в табл. 9; ветровые пояса, фермы, ветровые связи и железобетонные обвязки, рассчитанные по прочности и по деформациям на восприятие горизонтальной нагрузки, передающейся от стен.
Упругие опоры: покрытия и междуэтажные перекрытия при расстояниях между поперечными устойчивыми конструкциями, превышающих указанные в табл. 9, и при отсутствии ветровых связей.
Подразделение кладок на группы, указанные в табл. 9, подано в табл. 10.
В зависимости от жесткости опор здания в целом делятся соответственно на здания с жесткой и упругой конструктивной схемой. Жесткая конструктивная схема характерна, как правило, для многоэтажных гражданских зданий, упругая—для одноэтажных промышленных зданий.
2. Расчет стен зданий с жесткой конструктивной схемой.
Расчетная схема стен для многоэтажных зданий с жесткой конструктивной схемой при вертикальных нагрузках может быть принята в виде неразрезной вертикальной многопролетной балки с неподвижными опорами на уровне перекрытий, отстоящими друг от друга на расстоянии, равном высоте этажа (Hэт). Для упрощения расчета неразрезная балка заменяется однопролетными балками с шарнирными опорами на уровне опирания перекрытий (рис. 1).

Рис. 1. Расчетная схема стены и эпюра изгибающих моментов в ней от вертикальных нагрузок.
Расчетная ось стены (балки) принимается совпадающей с ее геометрической осью, проходящей через центр тяжести поперечных сечений стены.
В пределах каждого этажа на стену действует нагрузка Р от вышележащих этажей здания, нагрузка P1 от перекрытия, расположенного над рассматриваемым этажом, и собственный вес отдельных участков стены Q1 Q2, Q3. Нагрузка Р принимается приложенной на оси вышележащего этажа; P1 —в центре тяжести треугольной эпюры распределения давления под опиранием перекрытия (рис. 2); остальные нагрузки, действующие в пределах данного этажа, считаются приложенными с фактическими эксцентриситетами относительно расчетной оси.
Таким образом, каждое сечение стены испытывает действие продольной силы, равной сумме всех вышележащих вертикальных нагрузок, и изгибающего момента, изменяющегося по высоте стены по треугольнику (см. рис. 2).
Величина изгибающего момента на уровне низа перекрытия, расположенного под данным этажом, определяется по формуле
M1=P1e1±Pe
В этой формуле знак « + » принимается при уменьшении толщины стены вышележащего этажа за счет уступа с наружной стороны (рис. 3, в), знак «—» — за счет уступа с внутренней стороны (рис. 3, б). При неизменной толщине стены е=0 (рис. 3, а).
Расчет прочности стен производится на внецентренное сжатие, вызванное действием продольной силы N и изгибающего момента М.
Выбор расчетного сечения зависит от наличия и размеров проемов. В глухих стенах за расчетное принимается сечение I—I на уровне низа перекрытия с продольной силой N1 =Р + Р1 и максимальным изгибающим моментом M1 (см. рис. 2). В стенах с проемами опасным является сечение II—II на уровне низа перемычки, площадь которого значительно уменьшена. Продольная сила в этом сечении
NII=P+P1+Q1
а изгибающий момент
MII=M1H1/H
Часто наиболее опасным может оказаться сечение III—III, расположенное на расстоянии 1/3 от низа верхнего перекрытия, где изгибающий момент имеет значительную величину
MIII=(2/3)M1
а значение коэффициента φ, учитывающего влияние продольного изгиба, достигает минимума. Продольную силу NIII в этом сечении легко определить, прибавив к силе NII собственный вес части простенка.
3
 .
Расчет стен
зданий с упругой конструктивной схемой.
.
Расчет стен
зданий с упругой конструктивной схемой.
Здания с упругой конструктивной схемой рассматриваются как конструкции рамной системы (рис. 4). Стойками таких конструкций являются каменные стены и столбы, жестко заделанные в грунт на уровне пола, а ригелями — покрытия и перекрытия, принимаемые абсолютно жесткими в своей плоскости. Между собой стойки и ригели связаны шарнирно.
Сечение стоек может быть прямоугольным или тавровым (при наличии пилястр). Его ширина принимается в зависимости от характера приложения нагрузки, формы сечения и вида расчета (статический или конструктивный).
Если нагрузка от перекрытия или покрытия распределена равномерно по длине стены (например, при покрытии из железобетонного настила), за ширину сечения (b для прямоугольного или bп для таврового) при статическом и конструктивном расчете может приниматься вся ширина простенка, а при глухих стенах— вся длина стены между осями примыкающих к пилястре пролетов.
Если нагрузка от перекрытия сосредоточена на отдельных участках (опирание ферм, балок и пр.), то при статическом расчете ширину полки таврового сечения разрешается принимать
bn=bпл+(2/3)H ≤ bпл+12h, но не более ширины простенка.
bпл – ширина пилястры; H – высота стены; h – толщина стены.
Если толщина стены меньше 0,1 высоты сечения пилястры, сечение рассматривается как прямоугольное, без учета примыкающих к пилястре участков стены.
Ширина прямоугольного сечения b (стены без пилястр) при такой нагрузке в статическом расчете принимается
bn=b1+(2/3)H ≤ b1+12h, но не более ширины простенка.
Здесь b1 — ширина площади опирания опорных узлов фермы балок или опорных подушек под этими узлами.
В конструктивном расчете при сосредоточенной нагрузке за ширину сечения принимается величина, переменная по высоте стены:
Для таврового сечения ширина полки bп вверху принимается равной ширине пилястры bпл, а внизу — bп= bпл +H; в промежутках между этими крайними точками ширина bп меняется по линейному закону (см. рис. 5);
для прямоугольного сечения ширина b принимается аналогично с заменой ширины пилястры шириной опорной подушки b1.
При этом следует помнить, что ширина сечения стойки на каждом уровне не должна превышать ширины простенка.
Необходимый для статического расчета рамы модуль упругости кладки принимается Е=0,8Е0.
Изгибающие моменты и нормальные силы в различных характерных сечениях стоек рамы определяются по общим правилам строительной механики. При этом могут быть использованы таблицы, упрощающие этот расчет. По полученным усилиям проверяют несущую способность стен и столбов как работающих на внецентренное сжатие.
Кроме описанного расчета на эксплуатационные нагрузки (расчет в период эксплуатации), стены и столбы необходимо рассчитать и на нагрузки в стадии производства работ, когда покрытия еще не смонтированы (расчет на стадии монтажа). В этой стадии стены и столбы рассматриваются как консоли, заделанные в грунт и загруженные собственным весом и ветром.
Ширина сечения стен-консолей в этом случае принимается равной ширине простенков, а при глухих стенах — расстоянию между осями пилястр.
Е сли
несущая способность стен и столбов на
стадии монтажа не обеспечена, размеры
сечения не увеличивают, а предусматривают
специальные временные крепления.
сли
несущая способность стен и столбов на
стадии монтажа не обеспечена, размеры
сечения не увеличивают, а предусматривают
специальные временные крепления.

Рис. 5. К определению расчетной ширины сечения стен с упругой конструктивной схемой
