3.15. Является ли векторное поле соленоидальным?
3.15.1. Является ли векторное поле соленоидальным?
1) нет;
#2) да.
3.15.2. Является ли векторное поле соленоидальным?
1) нет;
#2)да
3.15.3. Является ли векторное поле соленоидальным?
1) нет;
#2) да;
3.15.4. Является ли векторное поле соленоидальным?
1) нет;
#2)
3.15.5. Является ли векторное поле соленоидальным?
1) нет;
#2) да.
3.16. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
3.16.1. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1) нет;
2)
;
3)
;
4)
;
#5)
3.16.2. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1) нет;
2)
;
3)
;
#4)
;
5)
;
3.16.3. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1) нет;
2)
;
3)
;
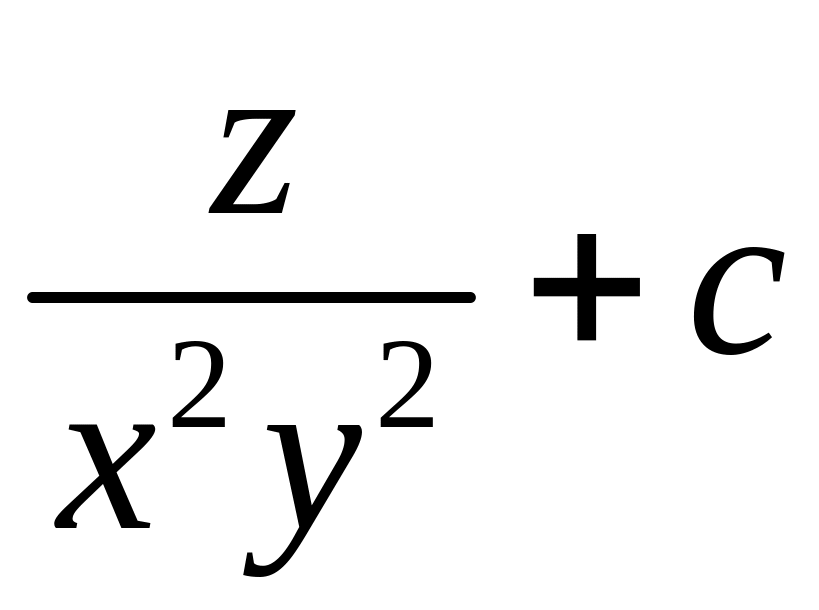#4)
;
5)
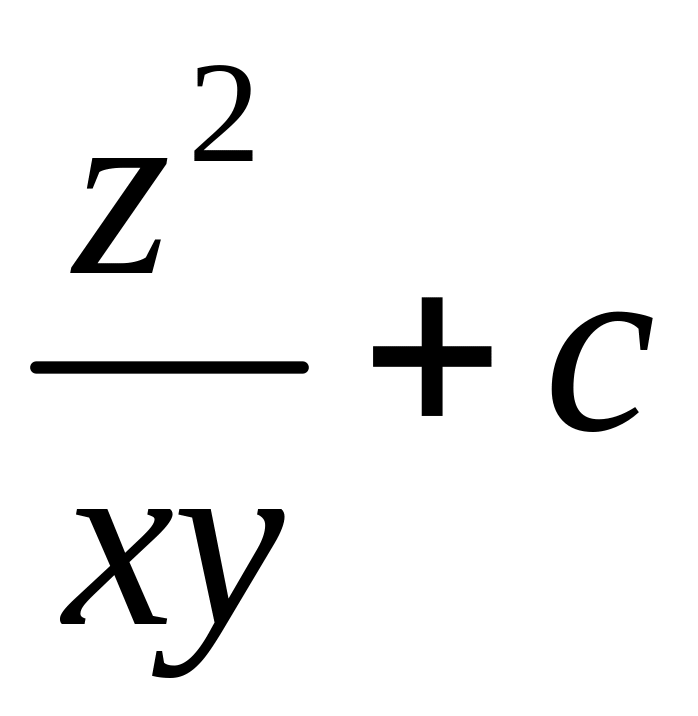
3.16.4. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1) нет;
2)
;
3)
;
4)
;
#5)
3.16.5. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1) нет;
2)
;
#3)
;
4)
;
5)
3.16.6. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1)
2)
3)
#4) не является
5)
3.16.7. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
#1)
2) не является
3)
4)
5)
3.16.8. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
#1)
2)
3)
4) не является
5)
3.16.9. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
1)
2)
3) не является
#4)
5)
3.16.10. Является ли векторное поле потенциальным? Если да, найти его скалярный потенциал.
#1)
2)
3)
4) не является
5)
3.17. Теория
3.17.1. Двойной
интеграл
,
где D
– прямоугольник
,
вычисляется по формуле:
1)
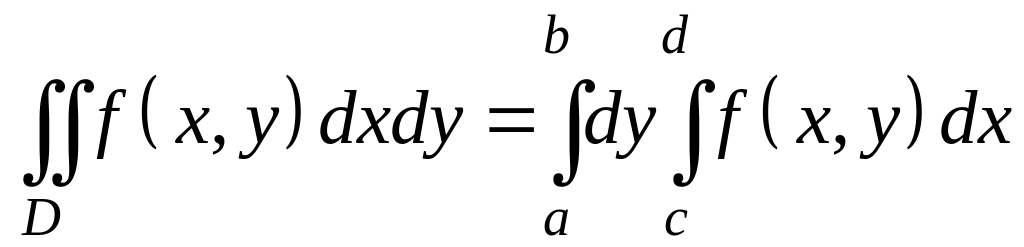
2)
#3)
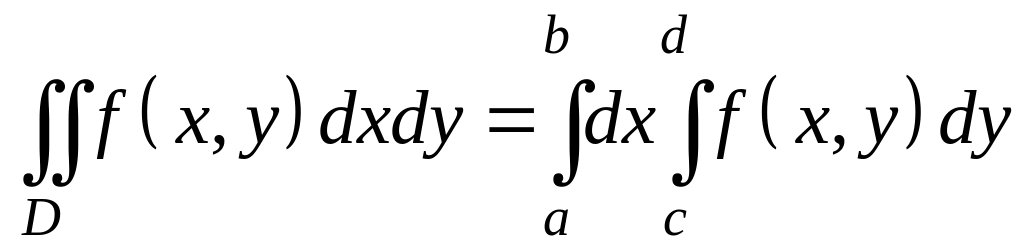
4)
5)
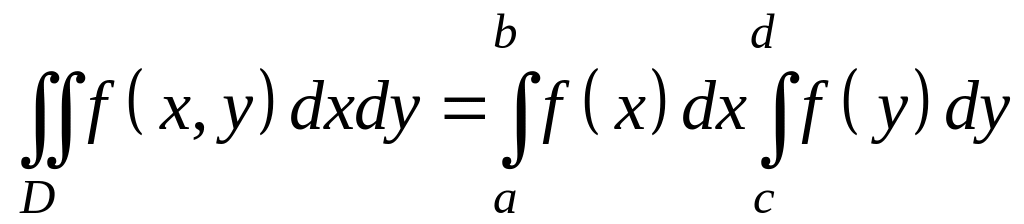
3.17.2. Двойной интеграл , где D – произвольная область,
ограниченная
сверху - графиком
,
а снизу – графиком
,и
прямыми
,
,
вычисляется по формуле:
1)
2)
#3)
4)
5)
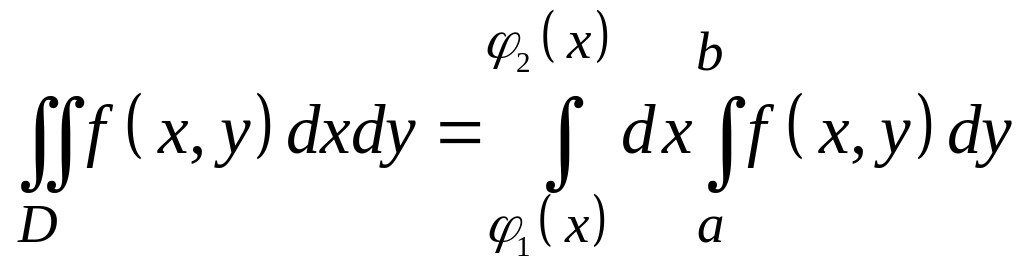
3.17.3. Двойной интеграл , где D – произвольная область,
в полярной
системе координат
вычисляется по формуле:
#1)
2)
3)
4)
5)
3.17.4. Для объемной области, представленной на рисунке, тройной интеграл
вычисляется по формуле:
1)
#2)
3)
4)
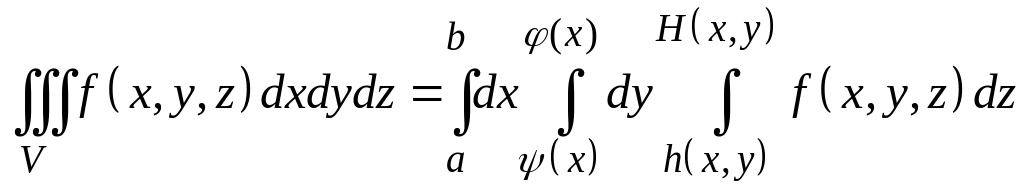
5)
3.17.5. Если в
пространственной области (V) задана
функция
и область (V) разбита с помощью сети
поверхностей на конечное число областей
,
имеющих соответственно объемы
,
и в каждой из областей
выбирается произвольно точка
,
в которой вычисляются значения
, то тройным интегралом называется:
1)
#2)
3)
4)
5)
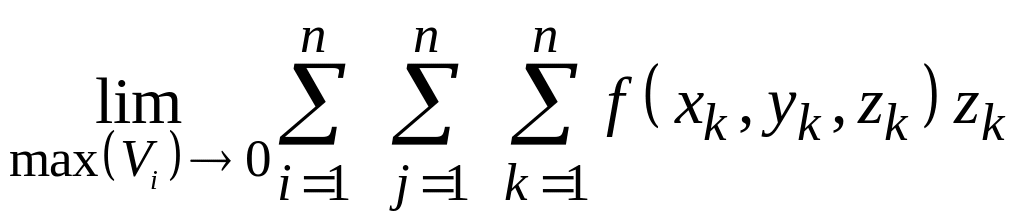
3.17.6.
Криволинейным
интегралом первого рода
называется
1)
,
где
;
#2)
;
3)
;
4)
;
5)
3.17.7. Если кривая
(L) задать параметрически, т.е.
,
,
то криволинейный интеграл первого рода
вычисляется
по формуле:
1)
;
#2)
;
3)
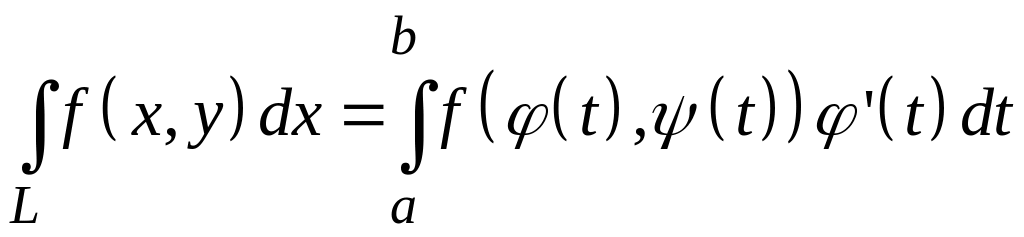
4)
5)
3.17.8. Если функции
и
непрерывны в области (D), ограниченной
контуром (L), то справедлива формула
Грина:
#1)
2)
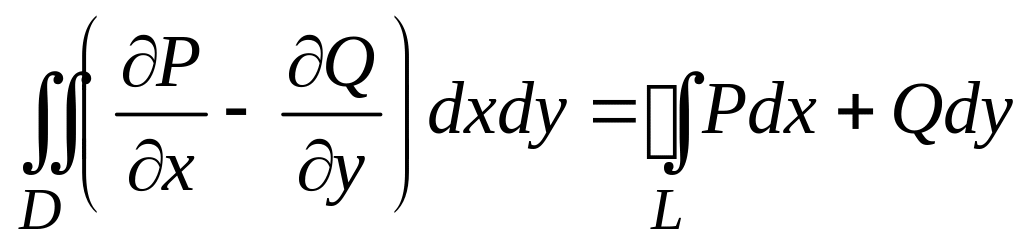
3)
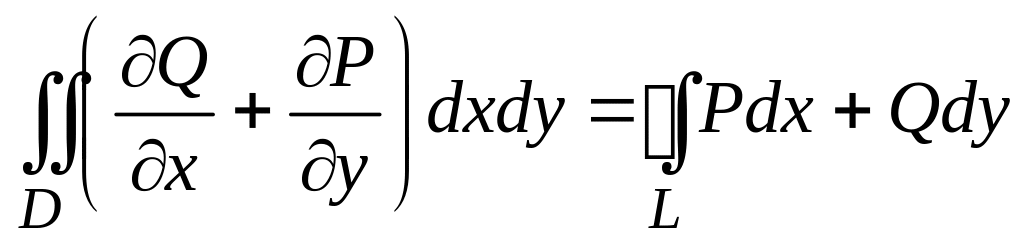
4)
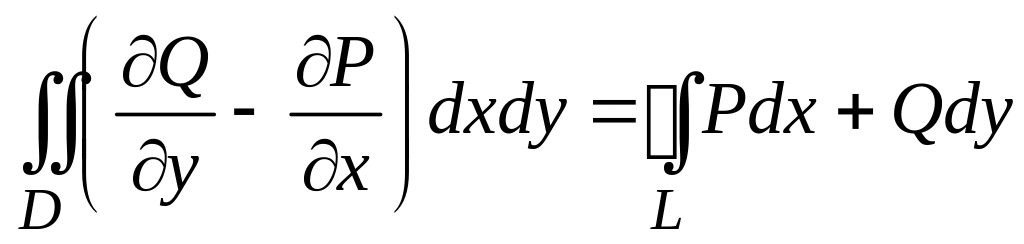
5)
.
3.17.9. Если кривая (L) задать параметрически, т.е. , , то криволинейный интеграл второго рода вычисляется
по формуле:
1)
2)
3)
4)
#5)
3.17.10. Если функция
,
непрерывна в замкнутой области
объема V,
то найдется точка
,
такая, что будет справедлива
формула:
#1)
2)
3)
4)
5)
3.17.11.Тройной
интеграл
,
где V
– произвольная область,
в
цилиндрической системе координат
вычисляется по
формуле:
1)
2)
3)
#4)
5)
3.17.12. Тройной интеграл , где V – произвольная
область,
в сферической системе координат
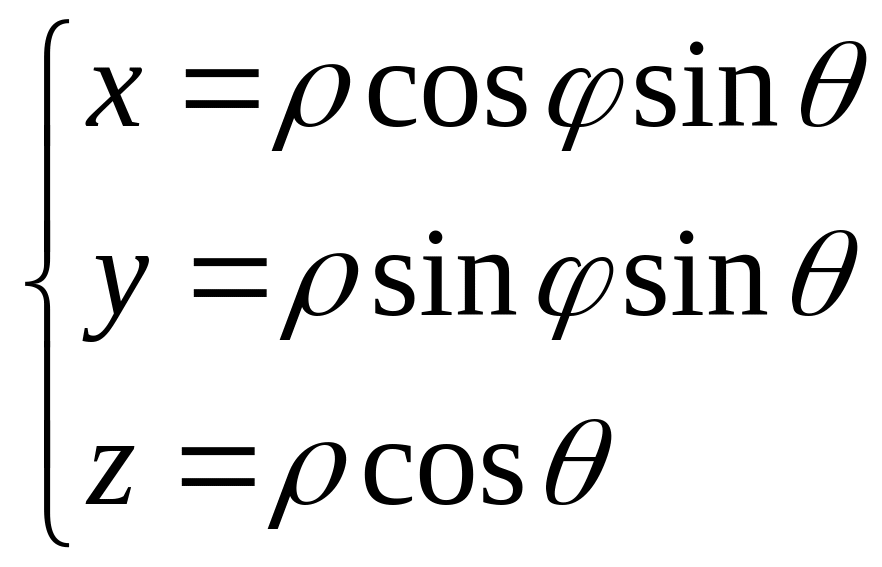
вычисляется по формуле:
1)
;
2)
#3)
4)
5)
3.7.13. Теорема Гаусса-Остроградского.
Если в некоторой
области
пространства
координаты вектора
непрерывны и имеют
непрерывные частные производные
,
то поверхностный интеграл по любой
замкнутой кусочно-гладкой поверхности
S,
лежащей в области
и ограничивающей область V,
равен тройному интегралу:
1)
2)
3)
4)
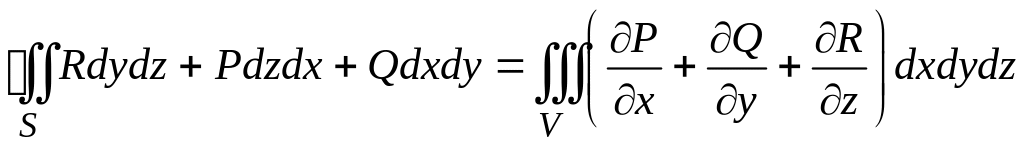
#5)
3.7.14. Для того, чтобы криволинейный интеграл по любому замкнутому
контуру L был равен нулю
необходимо и достаточно выполнение равенства
1)
2)
#3)
4)
5)
3.7.15. Для того, чтобы
криволинейный интеграл
не зависел от
пути интегрирования L в области, в которой функции и
непрерывны вместе со своими частными производными, необходимо и
достаточно выполнение равенства
1)
2)
#3)
4)
5)
3.7.16. Если функции
,
,
непрерывны вместе со
своими частными производными первого порядка в точках
поверхности S, то имеет место формула Стокса
1)
2)
3)
#4)
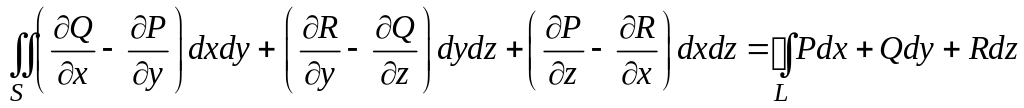
5)
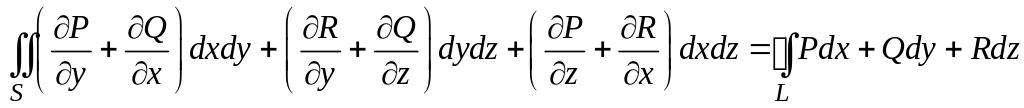
3.7.17. Если в некоторой области пространства координаты вектора
непрерывны и имеют непрерывные частные производные ,
то дивергенция
вектора
в
точке
определяется по формуле
#1)
2)
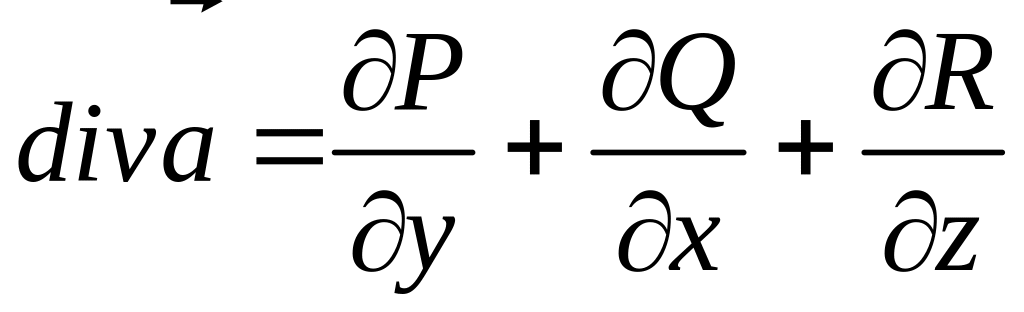
3)
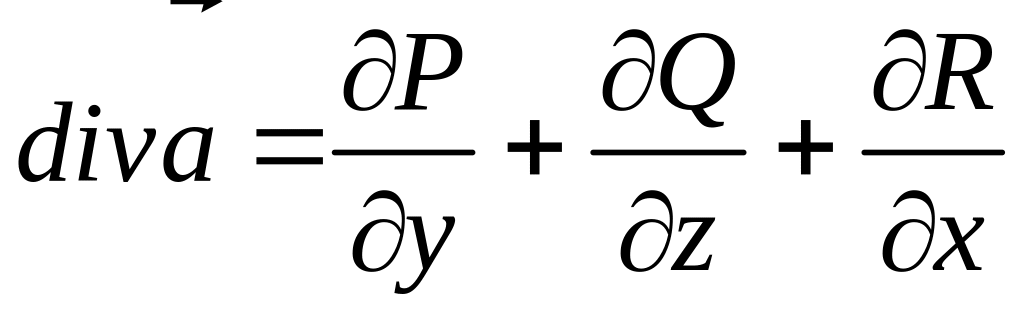
4)
5)
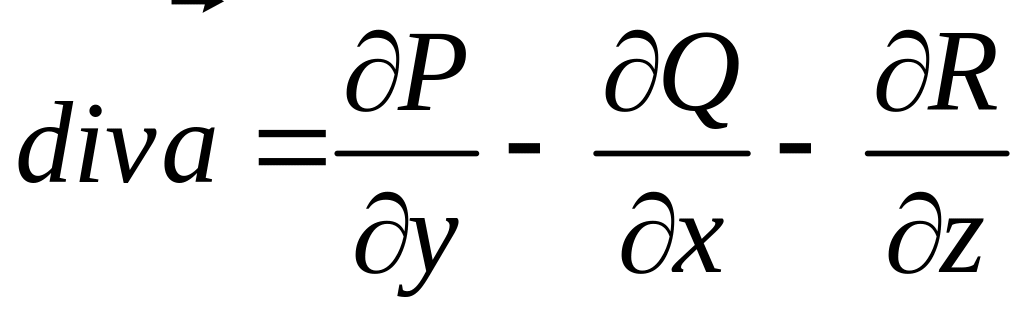
3.1.18. Производная
от функции
в
точке
по
направлению
вектора
,составляющим
с осями координат
соответственно
углы
вычисляется по формуле
1)
2)
#3)
4)
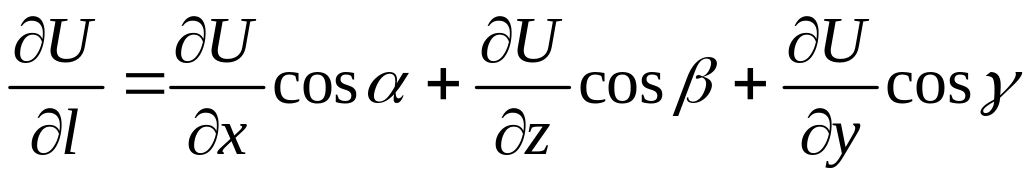
5)
3.1.19. Градиент функции указывает направление … функции.
1) наибыстрейшего убывания;
2) наибыстрейшего возрастания;
#3) наибыстрейшего изменения;
4) постоянства;
5) знакопостоянства.
3.1.20. Циркуляцией векторного поля
, будет
#1)
;
2) ;
3) ;
4)
5)
3.1.21. Если во всех точках М некоторой области дивергенция векторного
поля, заданного в , равна нулю, то данное поле является
1) эквипотенциальным;
2) безвихревым;
3) потенциальным;
4) вихревым;
#5) соленоидальным.
3.1.22. Если в некоторой области ротор векторного поля, заданного в ,
равен нулю, то данное поле является
1) эквипотенциальным;
2) трубчатым;
#3) потенциальным;
4) вихревым;
5) соленоидальным.
3.1.23. Векторное поле , заданное
в пространственной области V, называется потенциальным, если
существует
такая скалярная функция
,
что во всех точках
области V выполняется равенство
#1)
;
2)
;
3)
4)
5)
3.1.24. Векторным
потенциалом соленоидального векторного
поля
называется вектор
,
удовлетворяющий условию
1)
2)
#3)
4)
5)
3.1.25. Ротором векторного поля
называется
вектор, обозначаемый символом
и
определяемый
равенством
1)
2)
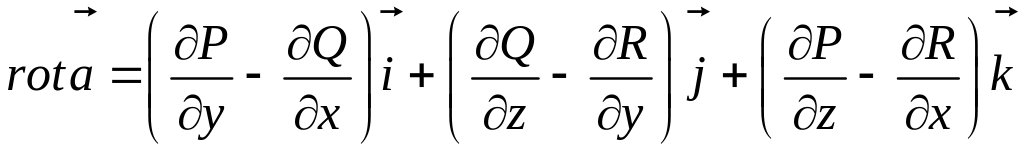
3)
4)
#5)
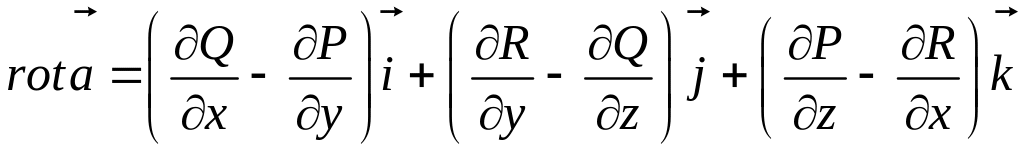
3.1.26 Потоком векторного поля
через ориентированную поверхность S называется ……..интеграл по
поверхности
S
от проекции вектора
на нормаль к этой
поверхности
двойной;
криволинейный;
#3) поверхностный;
4) тройной;
5) несобственный.
3.1.27. Градиент
скалярного поля
и его модуль в данной точке
поля определяются по формулам
1)
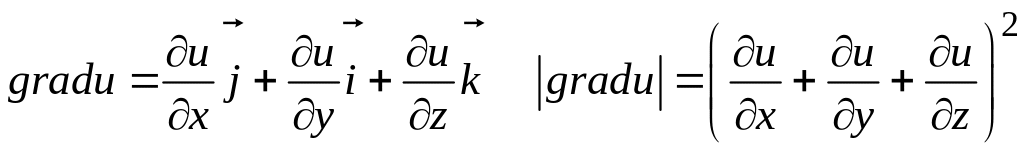
#2)
3)
4)
5)
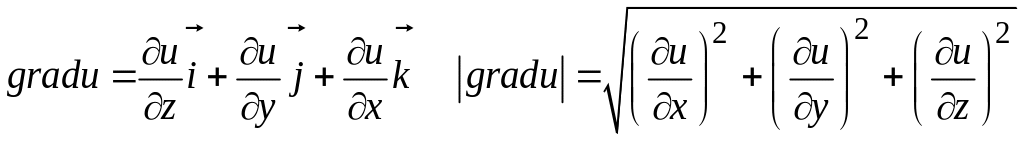
3.1.28 Модуль градиента равен…производной по направлению в данной
точке поля
наименьшей первой;
наибольшей второй;
наибольшей второй’
#4) наибольшей первой;
наименьшей первой