3.6. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
3.6.1. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
1) 0;
2)
;
#3)
;
4)
;
5)
3.6.2. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
1) 0;
2)
;
#3)
;
4) ;
5)
3.6.3. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
1) 0;
2) ;
#3)
;
4)
;
5)
3.6.4. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
1)
;
2) ;
3)
;
4)
;
#5)
3.6.5. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
1) ;
2)
;
3)
;
#4)
;
5)
3.6.6. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
,a
> 0
#1)
;
2)
;
3)
;
4)
;
5)
3.6.7. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
,
a
> 0
#1)
;
2)
;
3)
;
4)
;
5)
3.6.8. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
,
1) ;
#2) ;
3) ;
4) ;
5)
3.6.9. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
,
1) ;
2) ;
#3) ;
4) ;
5)
3.6.10. Вычислить объем области, ограниченной заданными поверхностями,
с помощью тройного интеграла в сферической системе координат
,
a > 0
#1) ;
2) ;
3) ;
4)
;
5)
3.7. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
3.7.1. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
;
#1) 1;
2) 2;
3) 3;
4)
;
5) 4
3.7.2. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
;
#1) 1;
2) 2;
3) 3;
4) 4;
5) 5
3.7.3. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
;
#1) 0;
2) 1;
3) 2;
4) 3;
5) 4
3.7.4. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
1) 0;
#2) ;
3) 1;
4) 2;
5) 3
3.7.5. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
1) 2;
2) 4;
3) 6;
4) 8;
#5) 16
3.7.6. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
;
#1) 0;
2) 1;
3) 2;
4) 3;
5) 4
3.7.7. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
;
1) 1;
#2) ;
3) 2;
4) 3;
5) 5
3.7.8. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
,
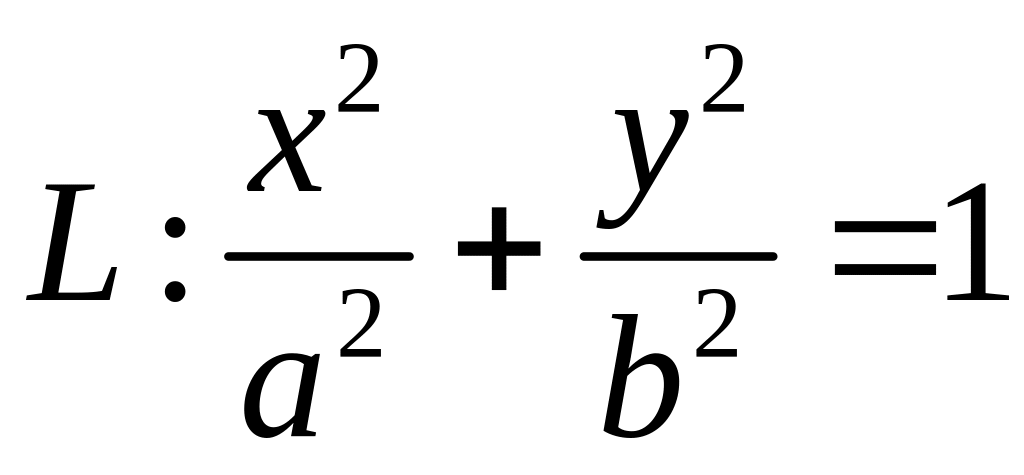против часовой стрелки
1) 1;
#2)
;
3) 4;
4) 6;
5) 9
3.7.9. Вычислить криволинейный интеграл по заданному контуру
интегрирования.
,
где
против часовой стрелки
1) 1;
2) 0;
#3) ;
4) ;
5)
3.7.10 Вычислить криволинейный интеграл по заданному контуру
интегрирования.
против часовой
стрелки
#1) 0;
2) 1;
3) 2;
4) 3;
5) 4