
- •Оглавление
- •§1. Неопределенный интеграл
- •1.1. Основные понятия неопределенного интеграла
- •1.2. Основные методы интегрирования Метод непосредственного интегрирования
- •Замена переменной
- •Интегрирование по частям
- •1.3. Интегрирование рациональных дробей
- •1.4. Интегрирование тригонометрических функций
- •1.5. Интегрирование иррациональных функций
- •1.6. Примеры интегралов, не выражающихся через элементарные функции
- •1.7. Задания для самопроверки №1
- •§2. Определенный интеграл
- •2.1. Основные понятия и методы решения определенного интеграла
- •1. Непосредственное интегрирование.
- •2.2. Приближенное вычисление определенного интеграла
- •Формула прямоугольников
- •Формула трапеций
- •Формула парабол (формула Симпсона или квадратурная формула)
- •2.3. Несобственные интегралы
- •1. Несобственные интегралы первого рода
- •2. Несобственные интегралы второго рода (интеграл от разрывной функции)
- •2.4. Задания для самопроверки №2
- •2.5. Геометрические приложения определенного интеграла
- •2.6. Физические приложения определенного интеграла
- •2.7. Экономическое приложение определенного интеграла
- •2.8. Химические приложения определенного интеграла
- •2.9. Задания для самопроверки №3
- •2.10. Вопросы и предложения для самопроверки Неопределенный интеграл
- •Определенный интеграл
- •Применение определенного интеграла
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Часть d
- •Часть e
- •Графики некоторых функций, заданных
- •Структура интегрального исчисления функции одной переменной
2.3. Несобственные интегралы
1. Несобственные интегралы первого рода
Если функция
![]() определена и непрерывна на любом отрезке
[a,b],
то несобственным
интегралом с бесконечным пределом или
несобственным интегралом первого рода
называется интеграл:
определена и непрерывна на любом отрезке
[a,b],
то несобственным
интегралом с бесконечным пределом или
несобственным интегралом первого рода
называется интеграл:
![]() или
или
![]() ,
или
,
или
![]() ,
с – произвольное число.
,
с – произвольное число.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если предел не существует или бесконечен, то несобственный интеграл называется расходящимся.
Теоремы о сходимости и расходимости:
Если на промежутке
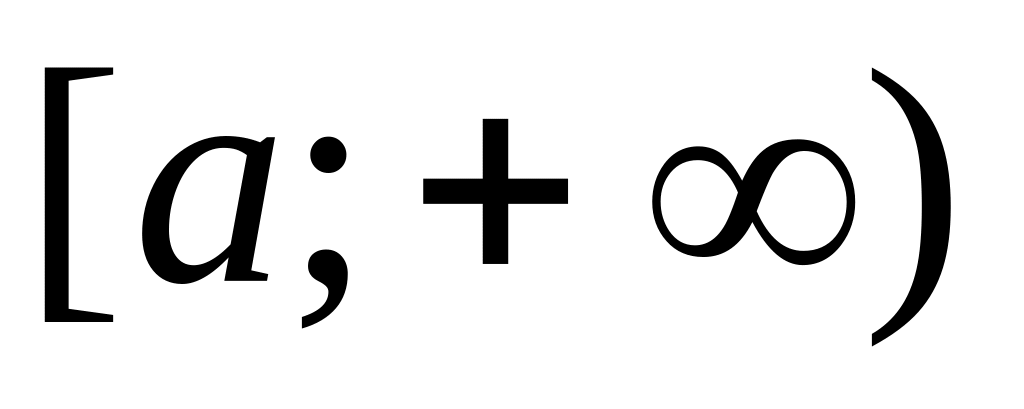 непрерывные функции
непрерывные функции
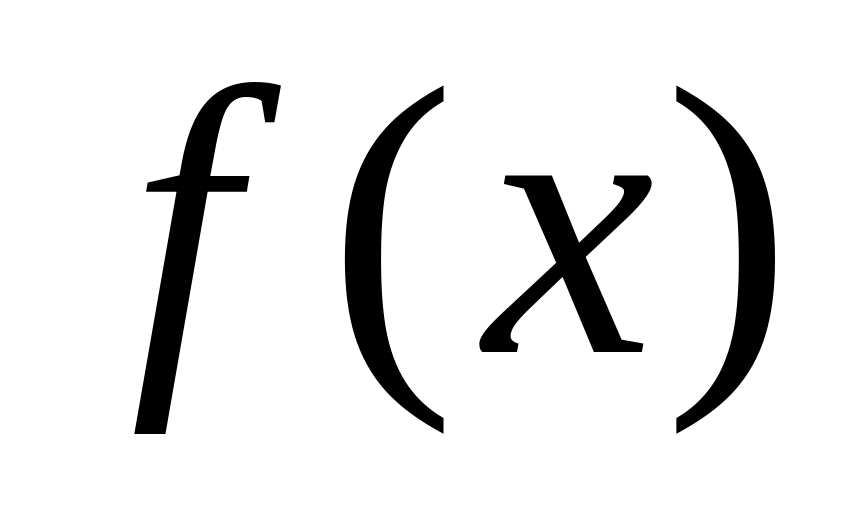 и
и
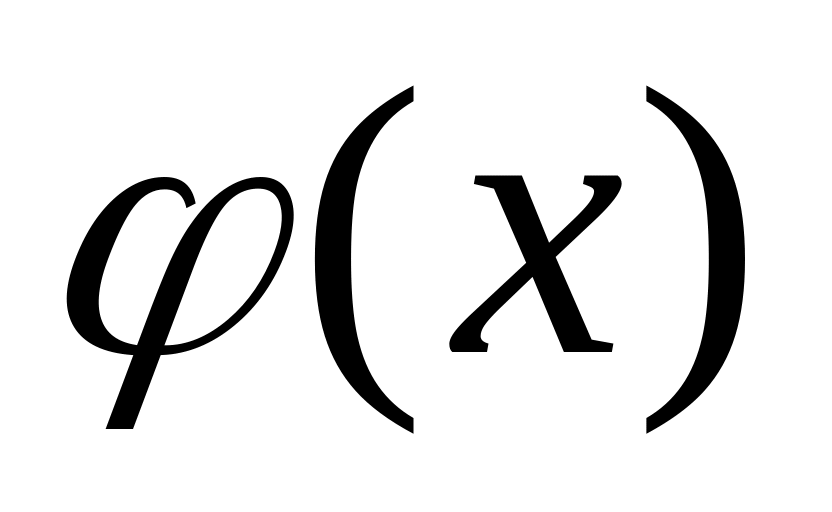 удовлетворяют условию:
удовлетворяют условию:
 ,
то из сходимости интеграла
,
то из сходимости интеграла
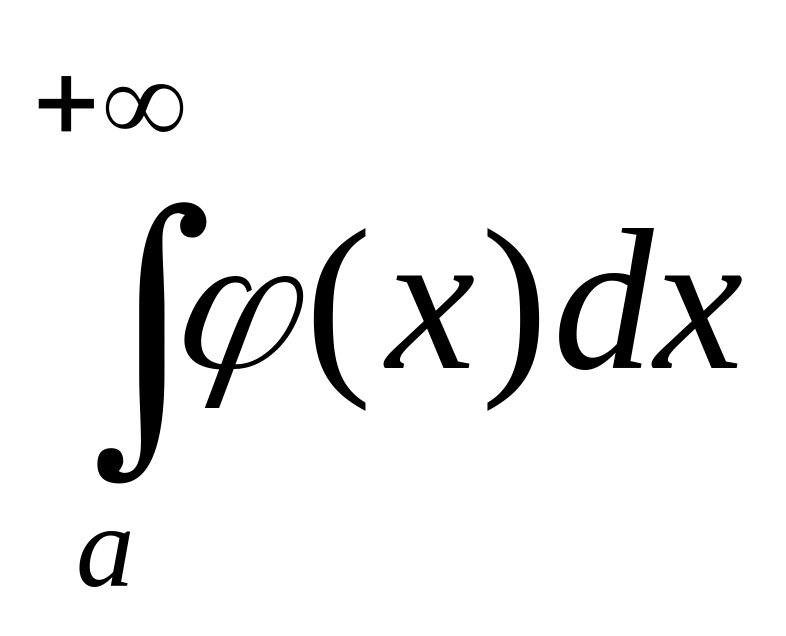 следует
сходимости интеграла
следует
сходимости интеграла
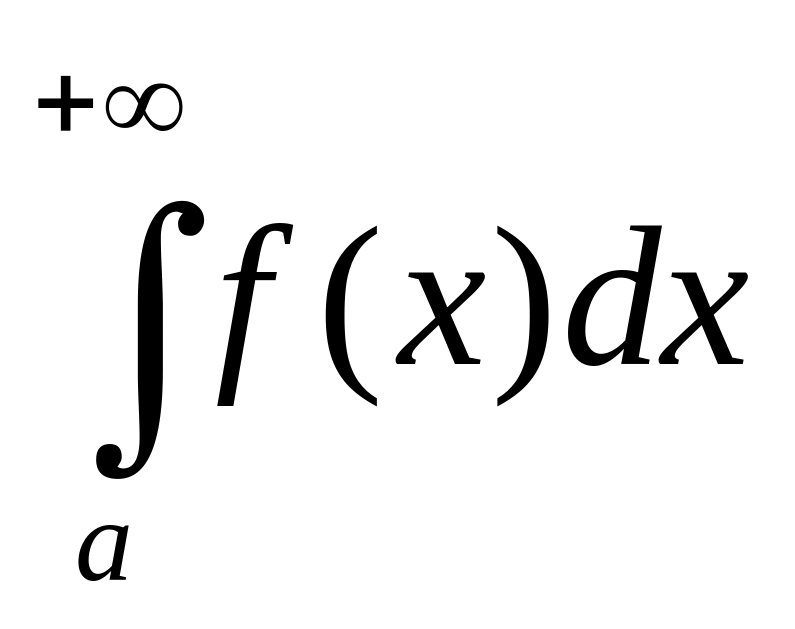 ,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).
,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).Если при
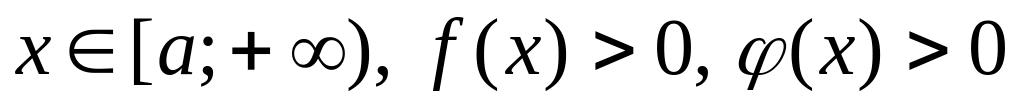 и существует конечные предел
и существует конечные предел
 ,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).
,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).Если сходится интеграл
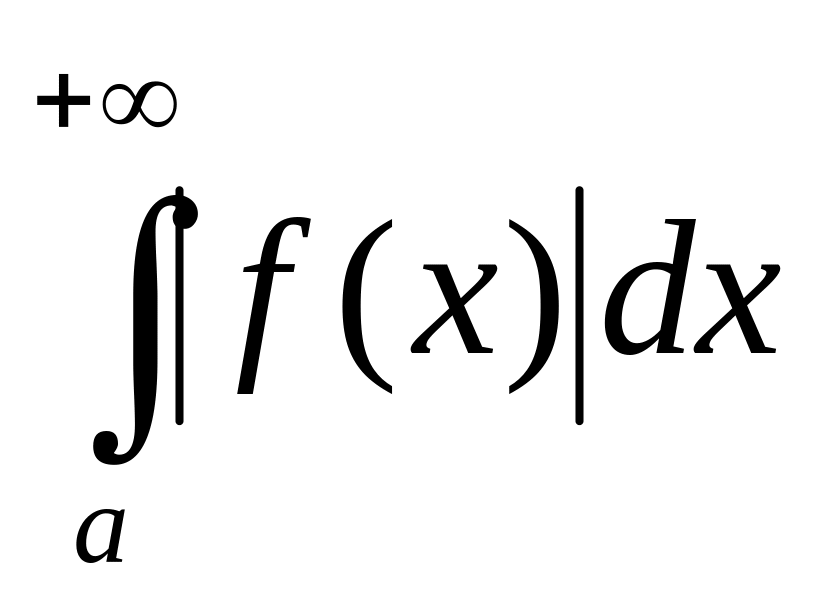 ,
то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
,
то сходится и интеграл
,
который в этом случае называется
абсолютно
сходящимся.
Примеры:
1.![]() -
не существует
-
не существует![]() несобственный интеграл расходится.
несобственный интеграл расходится.
2.
![]() - интеграл сходится.
- интеграл сходится.
2. Несобственные интегралы второго рода (интеграл от разрывной функции)
Если функция
непрерывна на промежутке
![]() и имеет разрыв II-го
рода при
и имеет разрыв II-го
рода при
![]() ,
то несобственным
интегралом неограниченной функции или
несобственным
интегралом второго родва
называется интеграл:
,
то несобственным
интегралом неограниченной функции или
несобственным
интегралом второго родва
называется интеграл:
![]() или
или
![]() ,
если функция терпит бесконечный разрыв
в точке
,
если функция терпит бесконечный разрыв
в точке
![]() .
.
Если функция
терпит разрыв II-го
рода во внутренней точке
![]() ,
то несобственным
интегралом второго рода
называют интеграл:
,
то несобственным
интегралом второго рода
называют интеграл:
![]() .
.
Замечание: внутренних точек разрыва II-го рода внутри отрезка может быть несколько.
Теоремы о сходимости и расходимости:
Если на промежутке функции и непрерывны, при терпит разрыв II-го рода и удовлетворяют условию: , то из сходимости интеграла
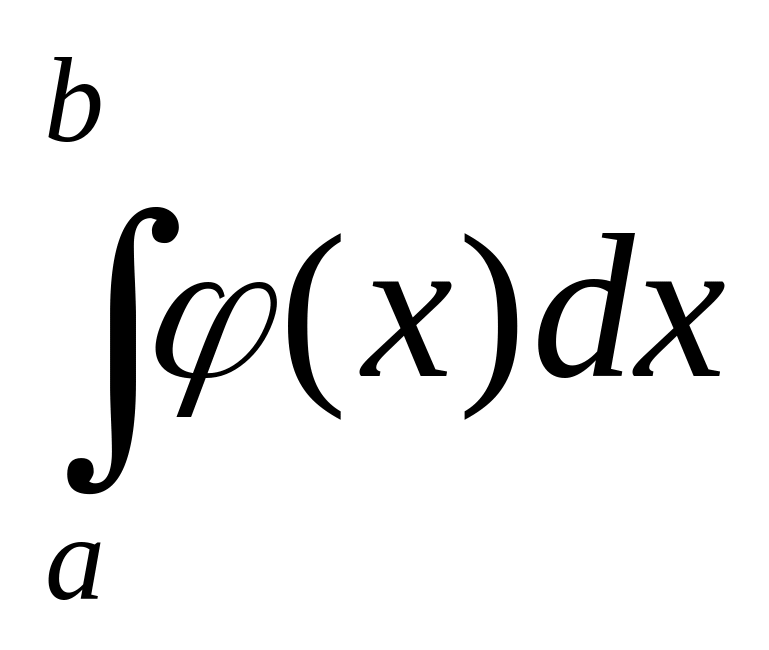 следует
сходимости интеграла
следует
сходимости интеграла
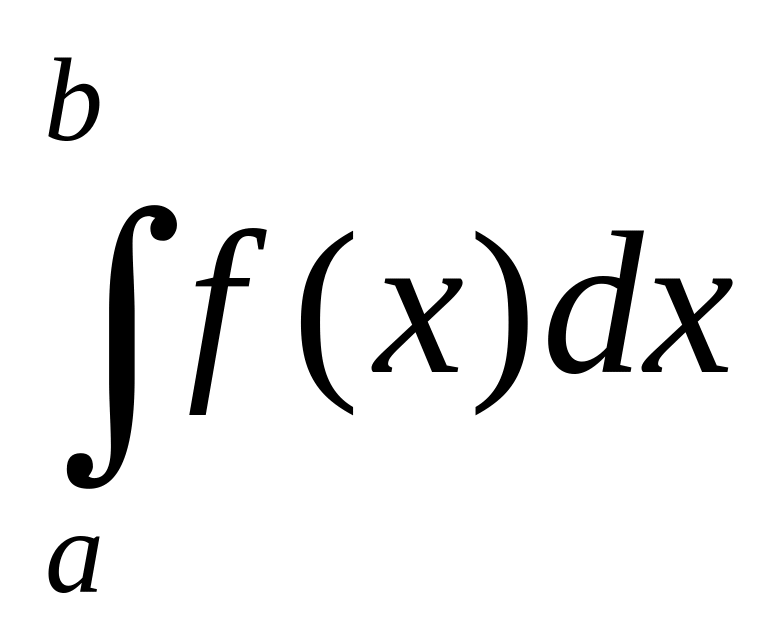 ,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).
,
а из расходимости интеграла
следует расходимость интеграла
(«признак сравнения»).Пусть функции и непрерывны на промежутке и в точке терпит разрыв II-го рода. Если существует предел
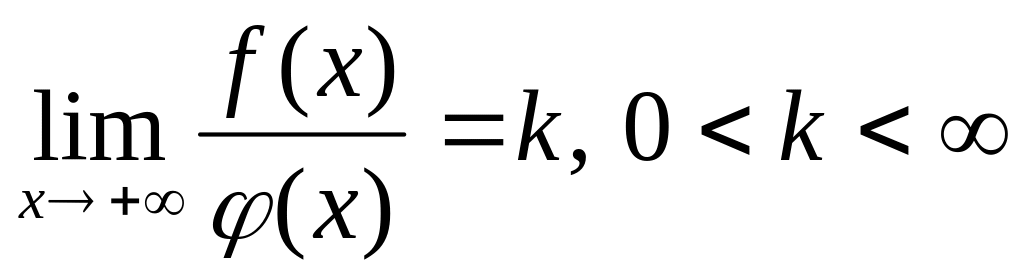 ,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).
,
то интегралы
и
сходятся или расходятся одновременно
(«предельный признак сравнения»).Если функция , знакопеременная на отрезке
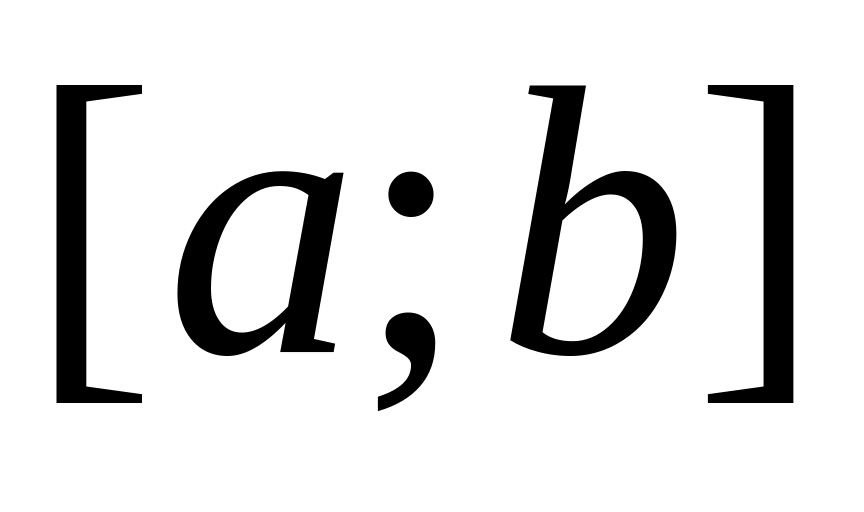 ,
имеет разрыв в точке
,
и несобственный интеграл
,
имеет разрыв в точке
,
и несобственный интеграл
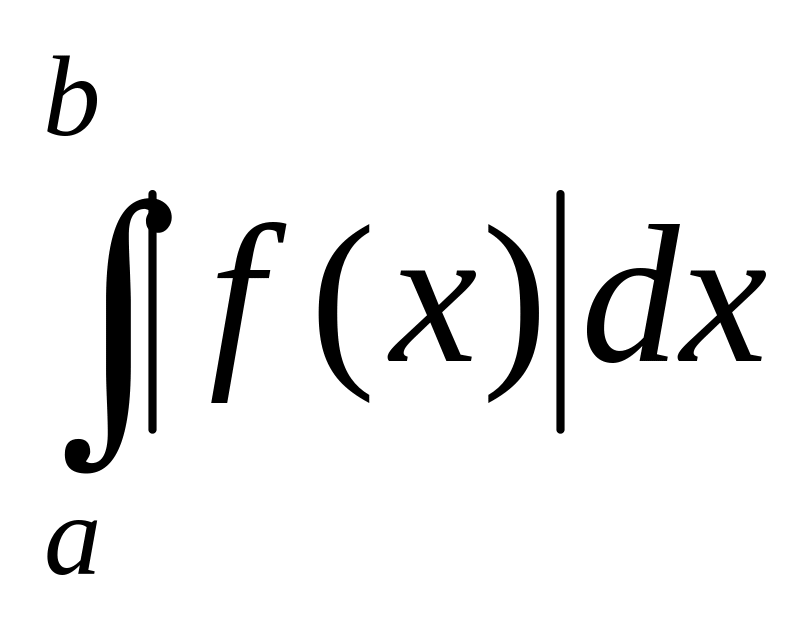 сходится, то сходится и интеграл
.
сходится, то сходится и интеграл
.
2.4. Задания для самопроверки №2
Вычислить:
1.
![]() Ответ:
6-2ln4
Ответ:
6-2ln4
2.
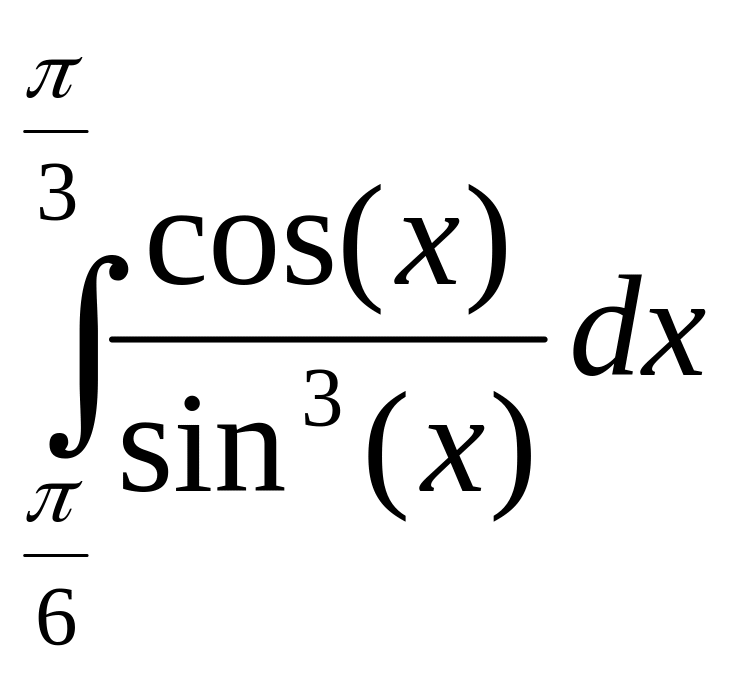 Ответ:
Ответ:
![]()
3.
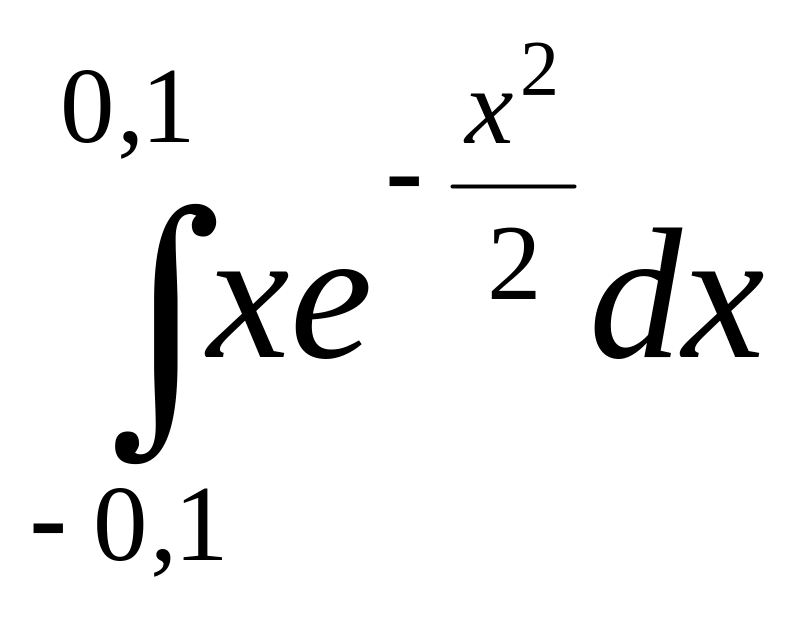 Ответ: 0
Ответ: 0
4.
![]() Ответ:
Ответ:
![]()
5.
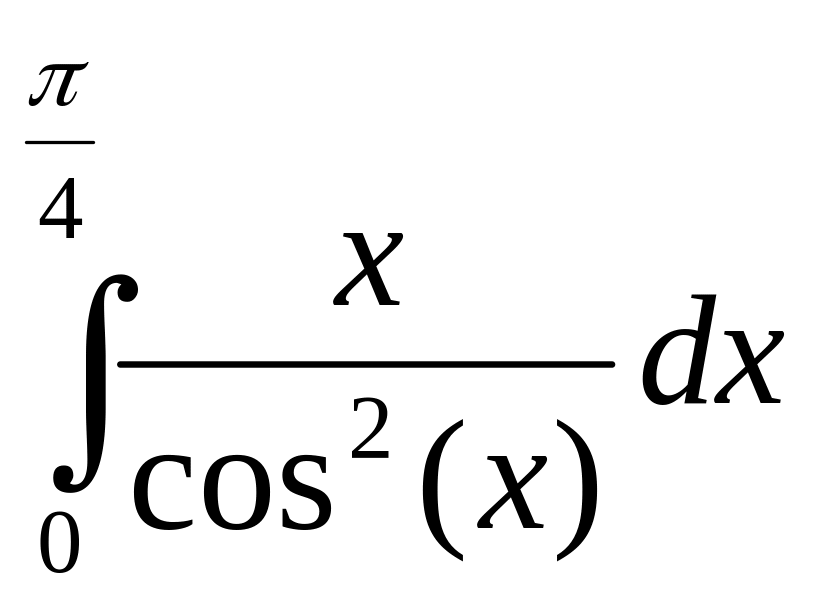 Ответ:
Ответ:
![]()
6.
![]() Ответ:
Ответ:
![]()
7.
![]() Ответ: π
Ответ: π
8. Исследовать на сходимость несобственные интегралы:
a)
![]() Ответ:
сходится
Ответ:
сходится
b)
![]() Ответ: расходится
Ответ: расходится
c)
![]() Ответ: сходится
Ответ: сходится
d)
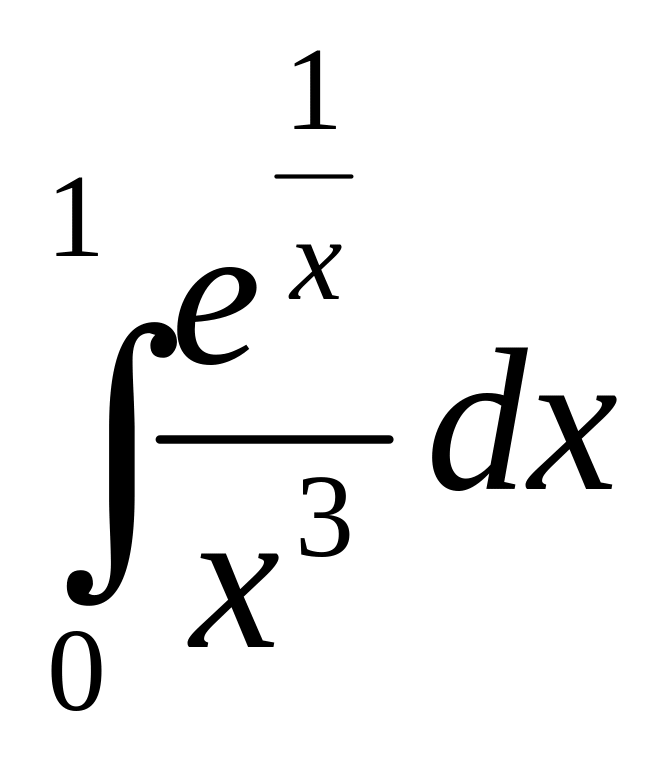 Ответ:
расходится
Ответ:
расходится
