Интегрирование по частям

Этот метод интегрирования основан на применении формулы дифференцирования произведения d(uv)=udv+vdu и вычислении затем интеграла . Из этого равества получаем формулу интегрирования по частям: .

Примеры:

a)

Интегирируется по частям: пусть ; тогда , . Следовательно, .

Еще раз интегрируется по частям: пусть тогда . Получаем,

.

b)

Интегирируется по частям: пусть ; тогда . Следовательно,

.

c)

Интегирируется по частям: пусть ; тогда , . Следовательно, .

Получившийся интеграл вычисляется методом замены переменной:

. Тогда

.

d)

Пусть . Тогда .

Интегирируется по частям: пусть ; тогда . Следовательно,

.

e)

Интегирируется по частям: пусть ; тогда , . Следовательно,

.

Обозначается, . Тогда .

Следовательно, .

f)

Интегирируется по частям: пусть ; тогда . Следовательно,

.

g)

Интегрируется по частям: пусть тогда . Следовательно, .

Еще раз интегрируется по частям: пусть тогда . Получается,

=

= .

Обозначается, . Тогда .

Следовательно,

h)

Интегрируется по частям: пусть тогда . Следовательно,

.

Еще раз интегрируется по частям: пусть тогда . Получается,

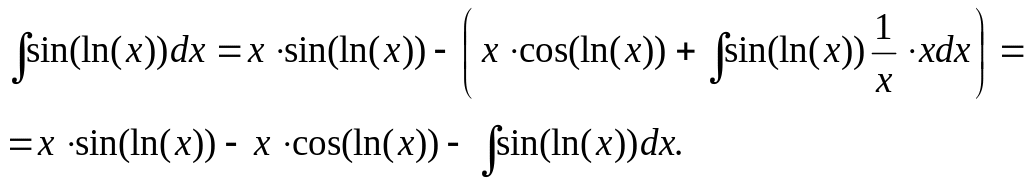
Обозначают, . Тогда

Следовательно,

k)

Интегрируется по частям: пусть

тогда .

Следовательно,

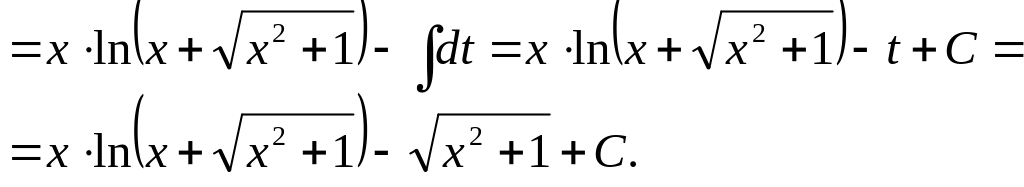
Приведем в таблице 2 некоторые распространённые случаи использования метода интегрирования по частям.

Таблица 2.

вид интеграла	метод интегрирования
, , .	За u принимается многочлен , а за dv все остальные подынтегральные выражения.
, , , , .	За dv принимается , а за u все остальные подынтегральные выражения.
, , , .	данные бесконечные интегралы, решаются как уравнения, после двукратного интегрирования по частям.
, , a > 0.	За dv принимается dх, а за u остальные подынтегральные выражения.

1.3. Интегрирование рациональных дробей

Дробно-рациональной функцией называется функция вида: , где - многочлен степени m, - многочлен степени n.

Замечание: Если m < n, то рациональную дробь называется правильной. Если m  n, то рациональную дробь называется неправильной.

Примеры:

a) = ;

b)

.

c)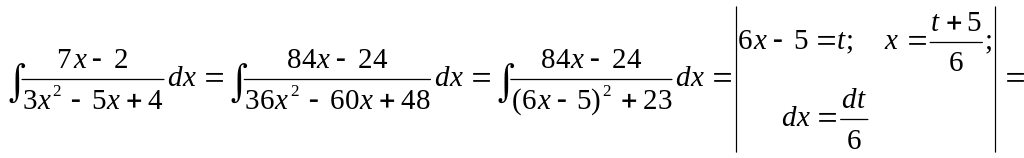

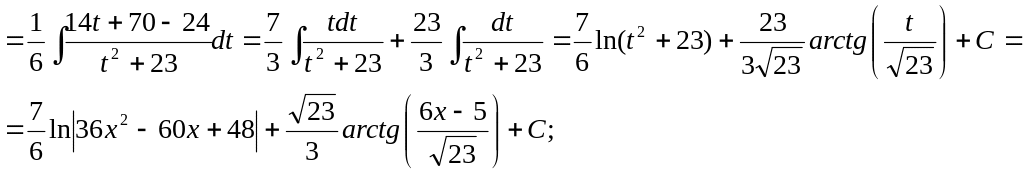
d)

.

Интеграл вычисляется с помощью:

• рекуррентной формулы: Она выведена в курсе математического анализа:

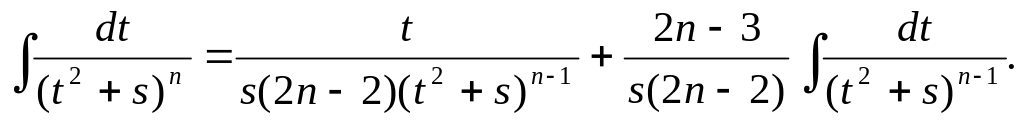
Следовательно,

.

• интегрирования по частям:

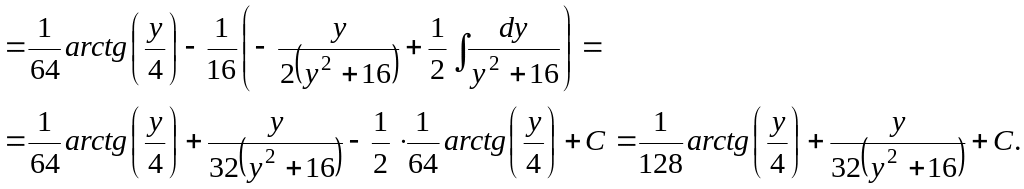
В таблице 3 приведены общие виды правильных рациональных дробей и способы их интегрирования с помощью замены переменной.

Таблица 3.

№	подынтегральное выражение	преобразования	замена	dx
I.
II.
III.
IV.				и раскладывается на сумму двух интегралов
V.
		и применяется рекуррентная формула

m, n – натуральные числа (m  2, n  2) и D <0.

Подынтегральные выражения не вошедшие в таблицу 3 интегрируются с помощью метода неопределенных коэффициентов.

Теорема (метод неопределенных коэффициентов). Если - правильная рациональная дробь, где знаменатель имеет вид:

P(x) = (x - a)^…(x - b)^(x² + px + q)^…(x² + rx + s)^ ) (причем множители типа x²+px+q неразложимы на действительные множители первой степени), то эта дробь может быть разложена на сумму простейших дробей:

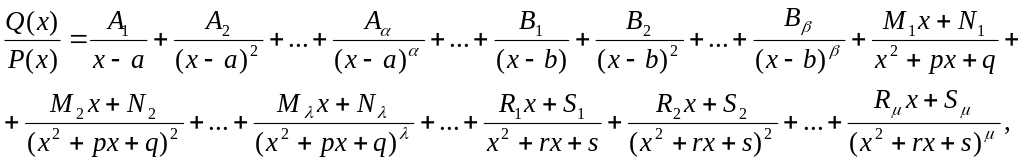где A_i, B_i, M_i, N_i, R_i, S_i – некоторые постоянные величины.

Примеры:

a) =

Подынтегральное выражение представляется в виде суммы простейших дробей .

После освобождения от знаменателей, получается:

.

Сгруппировываются члены с одинаковыми степенями:

В итоге получается:

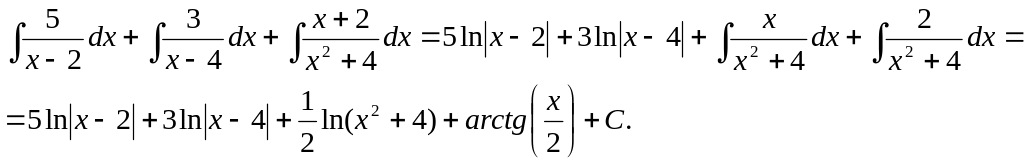
b) .

Так как дробь неправильная, то выделяется целая часть:

6 x⁵ – 8x⁴ – 25x³ + 20x² – 76x – 7 3x³ – 4x² – 17x + 6

6x⁵ – 8x⁴ – 34x³ + 12x² 2x² + 3

9x³ + 8x² – 76x - 7

9x³ – 12x² – 51x +18

20x² – 25x – 25

Следовательно,

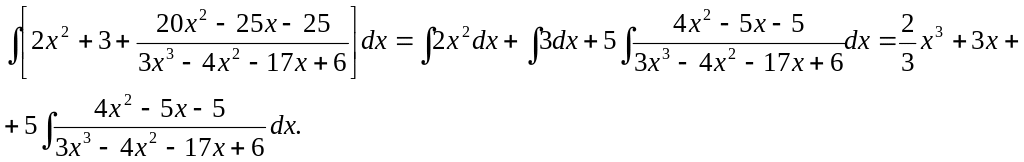Для нахождения корней уравнения применяем схему Горнера:

коэффициенты перед x
ре ше ние		3	– 4	– 17	6
	3	3	5	– 2	–
	– 2	3	– 1	–	–
	1/3	3	–	–	–

Получаются: .

Следовательно, корни этого уравнения: 3; -2; 1/3.

Отсюда .

Получившееся подынтегральное выражение раскладывается на элементарные дроби:

Применяем метод произвольных значений, суть которого состоит в том, что в полученное выражение подставляем поочередно (по числу неопределенных коэффициентов) значения х. Для упрощения вычислений принимают точки, при которых знаменатель дроби равен нулю. В нашем случае: 3, -2, 1/3. Получаем:

В итоге получаем:

=