Часть d

1. Вычислить площади фигур:

а)

;

б) ;

в)

2. Вычислить длины дуг кривых:

а) ;

б)

в)

.

3. Вычислить объемы тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:

Вычислить приближённо указанным методом , отрезок интегрирования разбить на 10 равных частей, сравнить с результатом непосредственного интегрирования:

а) прямоугольников;

б) трапеций;

в) Симпсона.

Вариант 5

Часть А

1.Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

2.Вычислить интегралы или установить расходимость:

а) ;

б) ;

в) ;

г) .

1.Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

2.Вычислить интегралы или установить расходимость:

а) ;

б) .

Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) .

1. Вычислить площади фигур:

а)

б)

в)

2. Вычислить длины дуг кривых:

а) ;

б) ;

в)

.

3. Вычислить объемы тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями:

Вычислить приближённо указанным методом, отрезок интегрирования разбить на 10 равных частей, сравнить с результатом непосредственного интегрирования:

а) прямоугольников;

б) трапеций;

в) Симпсона.

Вариант 6

Часть А

1.Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

2.Вычислить интегралы или установить расходимость:

а) ;

б) ;

в) ;

г) .

1.Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

2.Вычислить интегралы или установить расходимость:

а) ;

б) .

Найти неопределённые интегралы:

а) ;

б) ;

в) ;

г) .
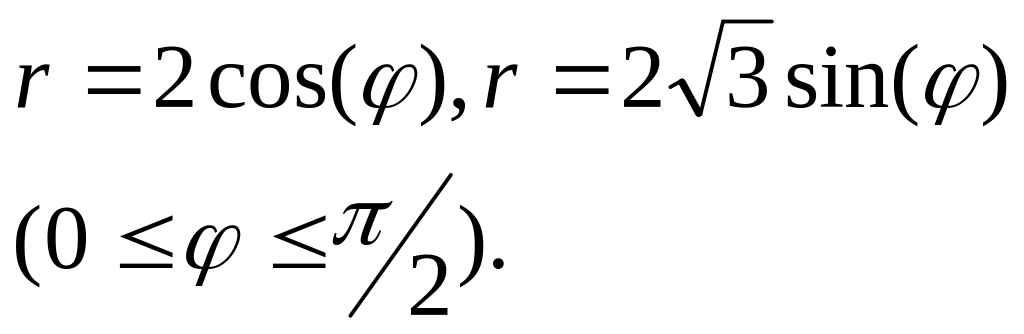
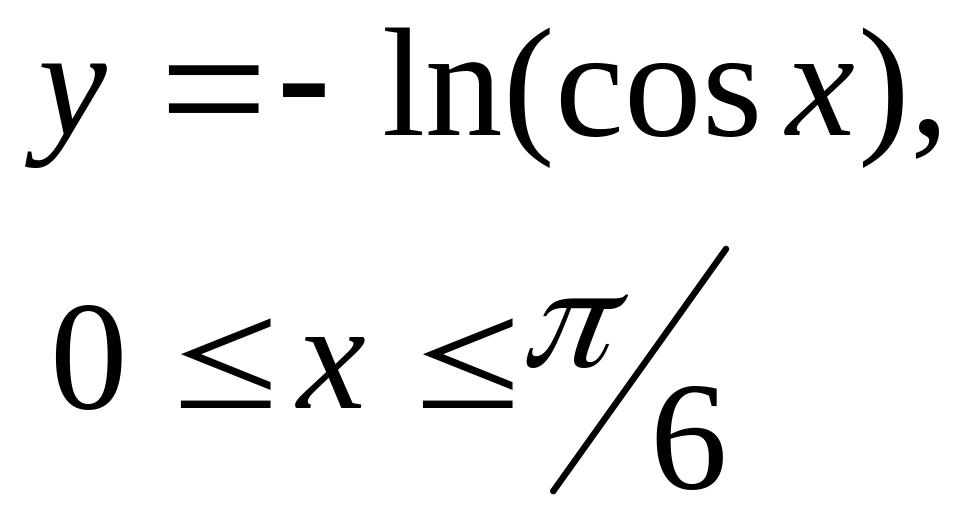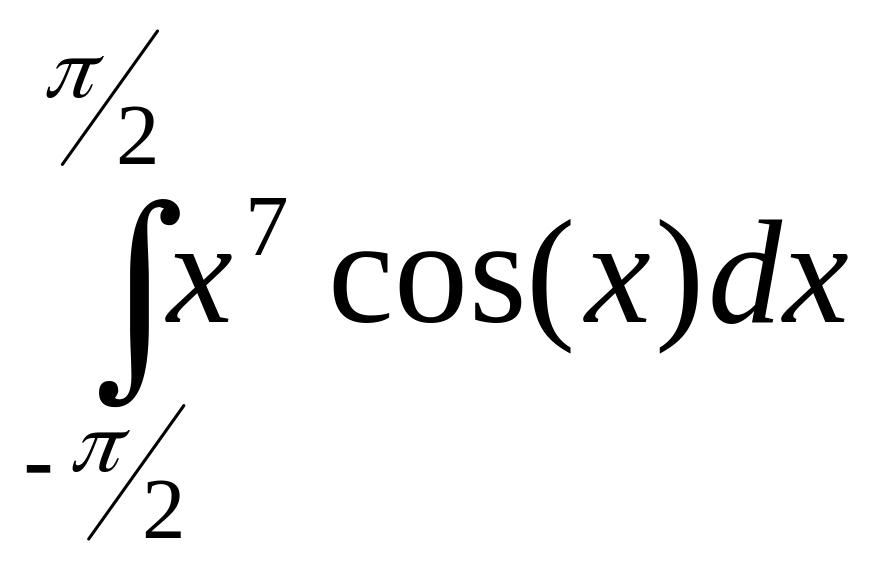