4. Соединение звеньев в системах автоматического управления

В реальных промышленных САУ соединение элементов между собой может быть довольно слож­ным. Однако любую сложную схему можно разбить на отдельные блоки с одним из трех типовых соединений: последовательным, параллельно-согласованным или параллельно-встречным.

Схема последовательного соединения звеньев представлена на рис. 5.5, а. Так как передаточная функция представляет собой отноше­ние преобразованных по Лапласу выходного сигнала звена к вход­ному, т.е.

то можно записать:

Следовательно, выходной сигнал каждого из звеньев в последо­вательной цени можно выразить через его передаточную функцию:

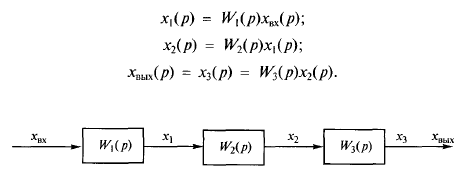
Рис. 5. Соединения звеньев схема цепи с последовательным соединением.

Последовательно подставляя в последнее уравнение выраже­ние входных сигналов, получим

т.е. передаточная функция цепи последовательно соединенных звеньев имеет вид

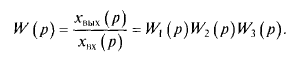
5. Постоянная времени

Типовая переходная функция апериодического звена, которая называется экспонентой. Любая экспо­нента обладает одним замечательным свойством: если к любой ее точке провести касательную, а затем точку касания и точку пере­сечения касательной с асимптотой, к которой с течением време­ни приближается экспонента, спроецировать на ось времени, то получится один и тот же отрезок на оси времени.

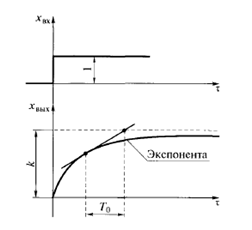
Рис 6. Постоянная времени

Эта проекция, называемая постоянной времени, соответствует коэффициенту Т₀, в передаточной функции и АФХ апериодическою звена, а орди­ната асимптоты, к которой стремится экспонента, — коэффици­енту k в его передаточной функции. Таким образом, по переход­ной функции легко найти коэффициенты k и Т₀ в передаточной функции апериодического звена.

Величина Т имеет размерность времени и называется по­стоянной времени. На рис. 333 представлены переходные процессы инерционного звена первого порядка при различных значе­ниях постоянной вре­мени.

Из кривых переход­ного процесса ясен фи­зический смысл постоян­ной времени звена. Она может быть определена как время, в течение которого выходная величина достигла бы своего нового устано­вившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

Постоянная времени инерционного звена первого по­рядка определяет динамические свойства звена. Чем она больше» тем медленнее протекает переходный процесс в зве­не, и наоборот. В частности, при Т = 0 процесс протекает в звене мгновенно и инерционное звено превращается в без­ынерционное усилительное. Время регулирования, т. е. время, в течение которого выходная величина практически будет равна новому установившемуся значению х_ВЫЛ = 0,95 kx_0вх равно примерно трем постоянным времени: t_p = 3Т. По истечении этого времени динамическая ошибка регулирования составляет всего 5% нового установившегося значения выходной величины.

Следует отметить также, что при t = Т значение выход­ной величины составляет 63% нового установившегося значения.

Постоянная времени звена геометрически (рис.6) определяется как проекция на ось времени отрезка каса­тельной к экспоненте, заключенного между точкой касания и точкой пересечения касательной с линией установившегося значения выходной величины. Длина этой проекции одина­кова для касательных, проведенных в любой точке экспонен­ты (точки О и О')