7. Выборочное уравнение прямой линии регрессии y на х имеет вид

y=	f(x)
152	53,03
197	96,03

Выборочное уравнение прямой линии регрессии X на Y:

x=	f(y)
62,2	167,03
92	187,49

Для построения эмпирических линий регрессии Y на Х и X на Y найдём условные средние у(х_i*) и х(у_i*) по формулам (32.3), используя корреляционную таблицу 8.

Итак, получены точки М_i (х_i*, у(х_i*)):

Mi(xi*,yср(xi*))
62,5	162,5
67,5	167,5
72,5	180,25
77,5	176,25
82,5	183,25
87,5	183,5
92,5	192,84

и точки N_i(y_i*,x^ср(y_i*)):

Ni(yi*,xср(yi*))
153,5	62,5
160,5	67,5
167,7	67,5
174,5	78,75
181,5	69,73
188,5	84,17
195,5	85,84

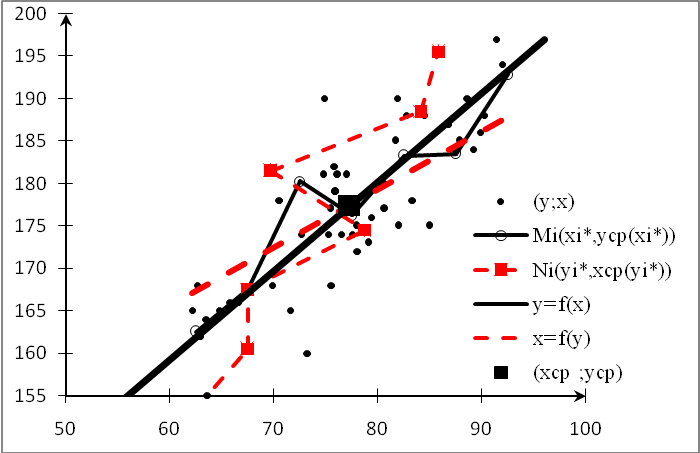
Напомним, что ломаная с вершинами в точках М_i (х_i*, у(х_i*) )есть эмпирическая линия регрессии Y и Х, а ломаная с вершинами в точках N_i(y_i*,x^ср(y_i*)) - эмпирическая линия регрессии X на Y.

На рисунке 7 также изображены прямые линии регрессии Y на X (сплошной линией) и Х на Y (пунктирной линией). На этом же рисунке отмечены выборочные точки (x_i,y_i), i =1, ... 50 (диаграмма рассеивания).

(xср	;yср)
77,3	177,44

Размещено на Allbest.Ru