5.1.2Расчет железобетонных элементов по образованию трещин

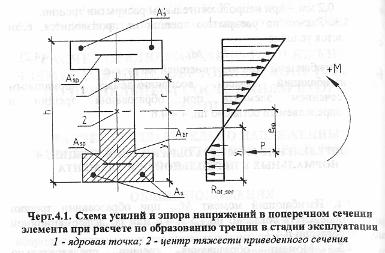
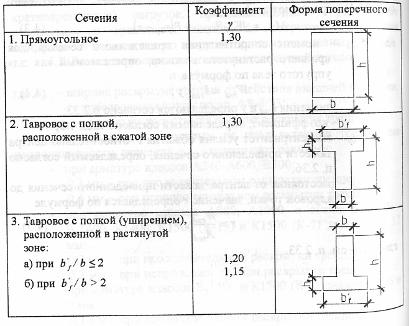
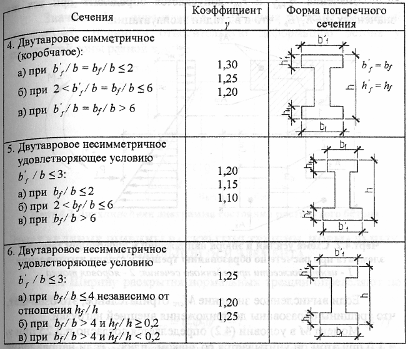
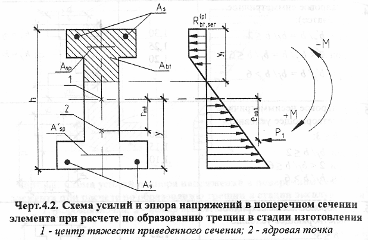
5.1.3Расчет железобетонных элементов по раскрытию трещин

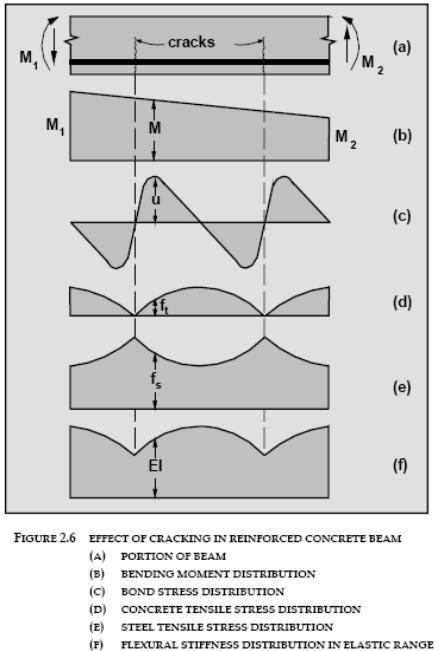
Так как трещины образуются в бетоне растянутой зоны, то ширина раскрытия трещин прямо пропорциональна относительному удлинению растянутых волокон элемента. При этом ширину раскрытия трещин принято считать на уровне оси растянутой арматуры. В этом случае за относительное удлинение растянутого волокна принимают относительное удлинение арматуры.

Обозначим расстояние между трещинами .

Относительное удлинение арматуры при растяжении получаем из выражения ,

в тоже время ,

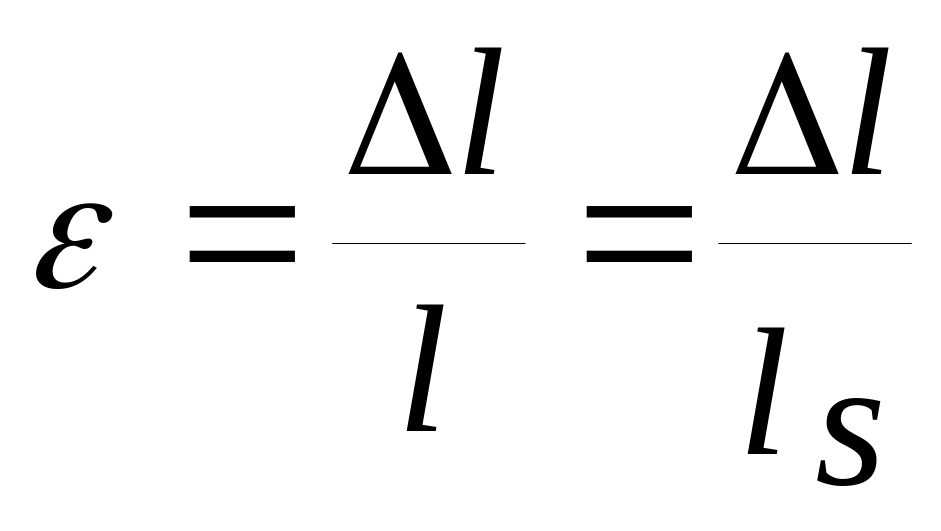полагая, что бетон является практически нерастяжимым материалом, получаем что удлинение арматуры происходит в основном на участке трещины, в этом случае получаем, тогда

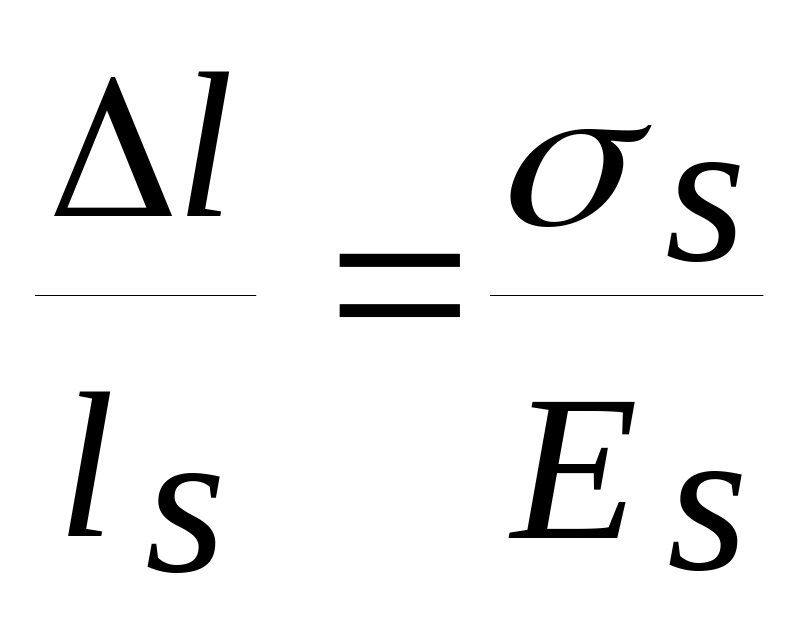, или

откуда получаем теоретическую формулу для определения трещин:

Согласно результатам экспериментов на ширину раскрытия трещин оказывает влиянием множество факторов:

1. Длительность действия нагрузки. Влияние данного фактора учитывают введением дополнительного коэффициента , который принимают равным при продолжительном действии нагрузки и при непродолжительном действии нагрузки.

2. Вид поверхности арматуры. Влияние данного фактора учитывают введением дополнительного коэффициента , который принимают равным для арматуры периодического профиля и канатной, - для гладкой арматуры.

3. Вид напряженного состояния элемента. Влияние данного фактора учитывают введением дополнительного коэффициента , который принимают равным для изгибаемых и внецентренно растянутых элементов и - для центрально растянутых элементов.

4. Неравномерность напряжений в арматуре между трещинами. Влияние данного фактора учитывают введением дополнительного коэффициента 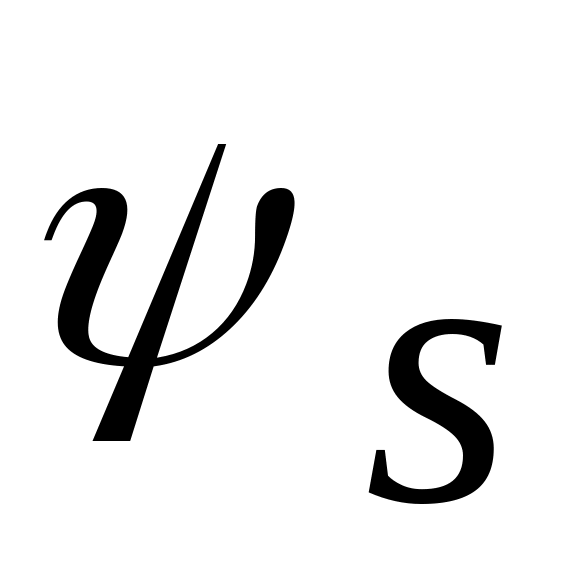, который допускается принимать равным . Если при этом ширина раскрытия трещин окажется больше допустимой, то значение уточняют по формуле . Где - напряжения в арматуре при образовании трещин.

Кроме перечисленных выше факторов, существует еще много факторов (усадка бетона, влажность воздуха и др.) которые не учитывают непосредственно при определении ширины раскрытия трещин.

Окончательно получаем выражение для определения ширины раскрытия трещин:

, т.е. формулу из [2].

С учетом того, что предварительно напряженные элементы, как правило, являются несимметрично обжатыми, т.е. не являются центрально растянутыми можно получить упрощенную формулу для предварительно напряженных элементов:

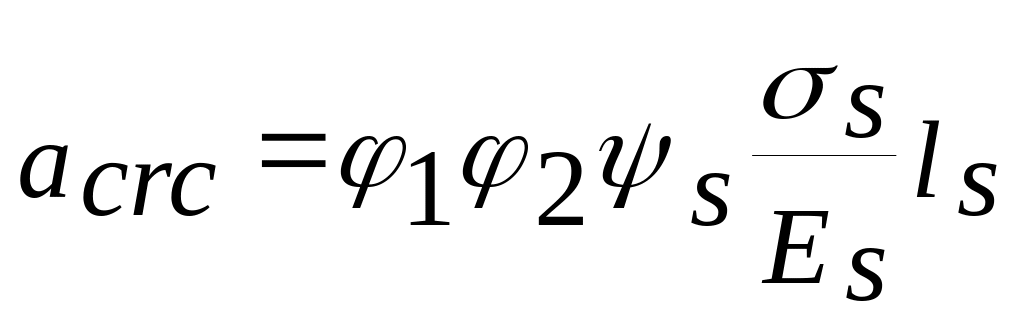, т.е. формулу 4.7 из [4].

Значения напряжений в растянутой арматуре определяют в соответствии со следующей схемой:

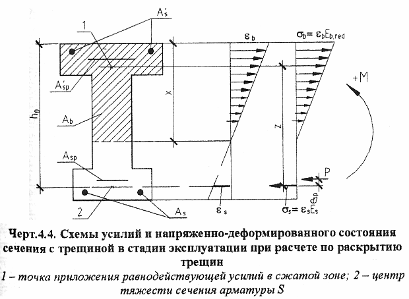
Так как для расчетов по второй группе предельных состояний (в том числе для расчета по раскрытию трещин) принимаются меньшие нагрузки чем для первой группы предельных состояний, а прочностные характеристики бетона и арматуры, наоборот, выше, то напряжения в бетоне сжатой зоны, как правило, не достигают расчетного сопротивления, т.е. . В этом случае более правильным является принимать линейное распределение напряжений в бетоне сжатой зоны.

Напряжения в растянутой арматуре для элементов без предварительного напряжения:

, так как , то получаем формулу:

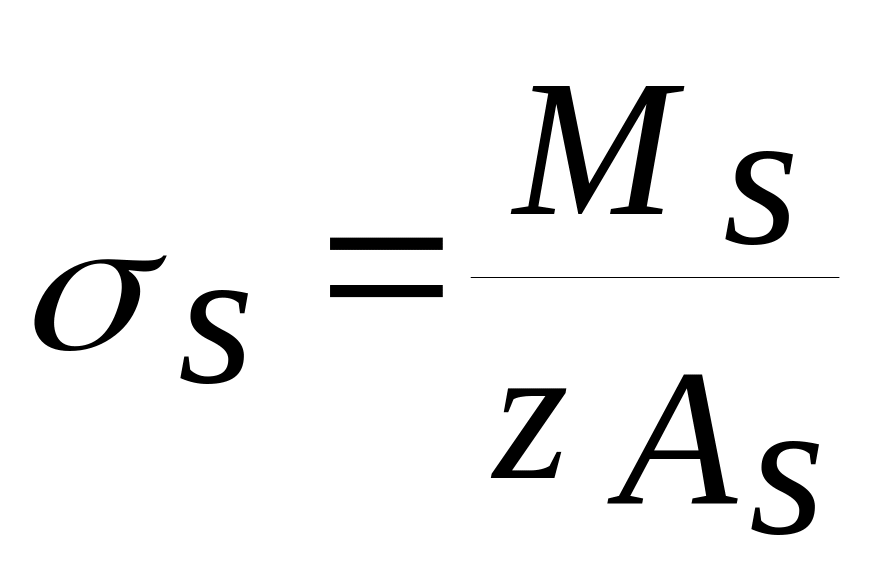, где - момент всех сил относительно оси проходящей через центр тяжести растянутой арматуры.

Для элементов без предварительного напряжения арматуры:

Для элементов с предварительным напряжением:

, при этом, если усилие предварительного обжатия приложена по оси рассматриваемой растянутой арматуры, т.е. , то .

Данный случай имеет место, если в растянутой зоне нет ненапрягаемой арматуры или она расположена на одной оси с напрягаемой, а также при отсутствии напрягаемой арматуры в противоположной зоне элемента.

Для элементов с предварительным напряжением раскрытие трещин вызывает удлинение арматуры только после преодоления предварительного обжатия, т.е.

или при наличии как напрягаемой, так и ненапрягаемой арматуры

Плечо внутренней пары выразим в зависимости от рабочей высоты сечения:

Параметр определяется по таблице 4.2. [4]. В зависимости от следующих величин: