4.1.1.3Практические методы расчета

4.1.1.4Примеры расчета

Пример 1

Дано:

Изгибающий момент: .

Размеры сечения: ,

Защитный слой бетона для растянутой арматуры:

Рабочая (растянутая) арматура: 220A400, ,

Бетон: В30,

Проверить прочность сечения на действие изгибающего момента

Решение:

Определяем предельное усилие в арматуре:

Определяем высоту сжатой зоны:

Определяем расстояние от растянутой грани до центра тяжести рабочей арматуры:

Определяем рабочую высоту сечения:

Выполняем проверку на переармирование:

, т.е. сечение не переармировано

Определяем плечо внутренней пары:

Определяем предельный изгибающий момент для рассматриваемого сечения:

Условие прочности:

Вывод: прочность сечения на действие изгибающего момента обеспечена.

Пример 2

Дано:

Изгибающий момент: .

Размеры сечения: ,

Защитный слой бетона для растянутой арматуры:

Рабочая (растянутая) арматура: 420A400, ,

Бетон: В30,

Проверить прочность сечения на действие изгибающего момента

Решение:

Определяем предельное усилие в арматуре:

Определяем высоту сжатой зоны:

Определяем расстояние от растянутой грани до центра тяжести рабочей арматуры:

Определяем рабочую высоту сечения:

Выполняем проверку на переармирование:

, т.е. сечение не переармировано

Определяем плечо внутренней пары:

Определяем предельный изгибающий момент для рассматриваемого сечения:

Условие прочности:

Вывод: прочность сечения на действие изгибающего момента не обеспечена.

4.1.1.5Элементы прямоугольного сечения со сжатой арматурой

Основные расчетные предпосылки при расчете железобетонных изгибаемых элементов такие же, как и для элементов без сжатой арматуры.

Рассмотрим усилия, действующие в поперечном сечении изгибаемого элемента при учете сжатой арматуры

,

Усилие в сжатой арматуре может быть определено следующим образом:

Усилие в растянутой арматуре может быть определено следующим образом:

Из уравнения равновесия (равенства нулю проекции всех сил на продольную ось элемента) следует, что:

, т.е.

или

Запишем уравнение моментов всех сил относительно оси растянутой арматуры

или

в данном случае ,

получаем

или

как видим из приведенного выше уравнения, разрешение его относительно возможно только при исключении еще одного неизвестного – , т.е. на данном этапе необходимо задаться площадью сжатой арматуры. Наиболее рационально площадь сжатой арматуры назначать таким образом, чтобы сумма площадей сжатой и растянутой арматуры была минимальной, в этом случае усилие в бетоне принимается равным предельному значению, т.е.

тогда

откуда

так как

, получаем

, откуда

, т.е. формулу 3.24 из [2].

так как и

получаем

или

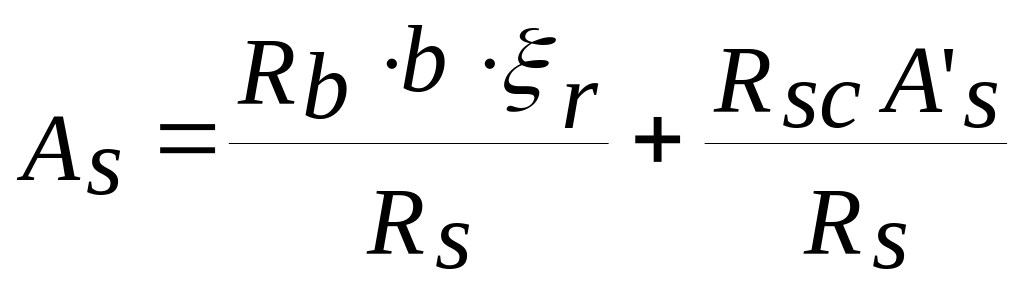
в случае если расчетное сопротивление арматуры сжатию и растяжению совпадает, т.е. , получаем частный случай приведенной выше формулы:

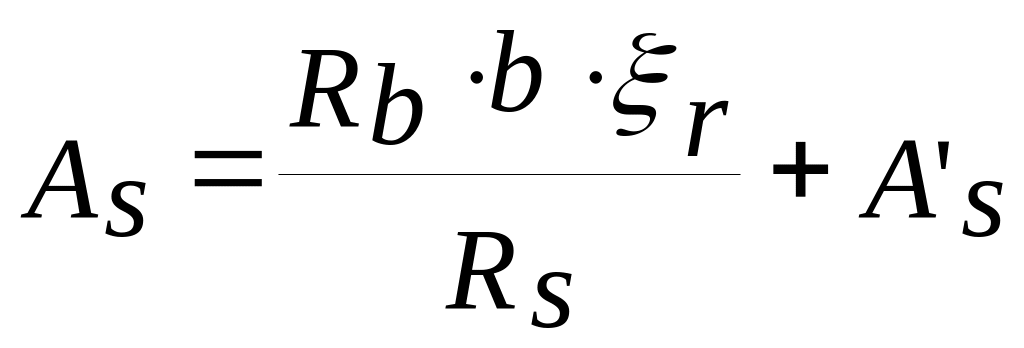, т.е. формулу 3.25 из [2].

более точно площадь растянутой арматуры можно найти следующим образом. Высоту сжатой зоны бетона найдем из уравнения

находим корни данного уравнения

обозначив

- относительная величина изгибающего момента

получаем

Очевидно, что не может являться корнем уравнения, т.к. выражение в скобках превышает 1, и высота сжатой зоны превысит рабочую высоту сечения, что не является искомым корнем. Таким образом, единственным верным корнем уравнения является:

так как

или

в случае, если расчетное сопротивление арматуры сжатию и растяжению совпадает, т.е. , получаем частный случай приведенной выше формулы:

, т.е. формулу 3.26 из [2].