4.1.1.2Элементы прямоугольного сечения без сжатой арматуры и без предварительного напряжения рабочей арматуры

Рассмотрим усилия, действующие в поперечном сечении изгибаемого элемента

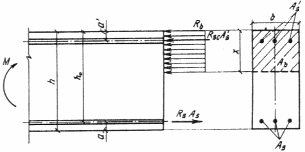
Так как напряжения в бетоне равномерно распределены в пределах сжатой зоны, усилие в сжатой зоне бетона может быть определено следующим образом:

,

где:

- площадь сжатой зоны бетона

- ширина элемента,

- высота сжатой зоны.

Усилия в растянутой арматуре могут быть определены следующим образом:

Из уравнения равновесия (равенства нулю проекции всех сил на продольную ось элемента) следует, что:

, т.е.

или

Как видно из приведенной выше формулы, на данном этапе для одного уравнения имеется два неизвестных – высота сжатой зоны бетона и площадь растянутой арматуры. Для разрешения этого противоречия введем еще одно условие равновесия – равенства нулю моментов всех сил относительно любой точки. Для данного условия равновесия не принципиально, относительно какой точки оно записывается, однако наиболее удобно записывать его для точки расположенной на оси растянутой арматуры, в этом случае:

, т.е.

где - плечо внутренней пары сил.

Плечом внутренней пары сил называется расстояние между равнодействующими усилий в растянутой арматуре и сжатом бетоне.

или

Учитывая, что напряжения по сжатой зоне бетона распределены равномерно, получаем:

, где - рабочая высота сечения.

Рабочей высотой сечения называется расстояние между равнодействующей усилий в растянутой арматуре и сжатой гранью сечения.

тогда

т.е. решение задачи сводится к решению квадратного уравнения с нахождением высоты сжатой зоны бетона.

Запишем данное уравнение в классическом виде:

раскрыв скобки, получаем:

находим корни данного уравнения

обозначив

- относительная величина изгибающего момента

получаем

Очевидно, что не может являться корнем уравнения, т.к. выражение в скобках превышает 1, и высота сжатой зоны превысит рабочую высоту сечения, что не является искомым корнем. Таким образом, единственным верным корнем уравнения является:

так как , то

, или

Данная формула содержится в [2] и [4] для определения требуемой площади рабочей арматуры железобетонных изгибаемых элементов прямоугольного сечения

Можно записать полученную выше формулу в другом виде.

как указано выше

или

откуда

или

Введем обозначение:

- относительная высота сжатой зоны

тогда можно записать, что

и

откуда

и далее найти требуемую площадь растянутой рабочей арматуры

из формулы

данный подход позволяет в прямом виде получить плечо внутренней пары, которое очевидно, всегда меньше рабочей высоты сечения, что является дополнительной проверкой правильности решения.

Можно также ввести обозначение

, тогда или

Чаще всего, значение , поэтому для приблизительных расчетов можно принимать и тогда

, однако данной формулой можно пользоваться только для приблизительных расчетов.

Проверку на переармирование производят из условия , где - граничная относительная высота сжатой зоны.

При проектировании изгибаемых элементов, когда площадь арматуры и высота сжатой зоны бетона неизвестны, удобно пользоваться величиной , из выражения приведенного выше

, получаем или, выразив , получим

Вычисленные по данной формуле значения в табличной форме в зависимости от класса арматуры также приведены в [2] в таблице 3.2.

при элемент является непереармированным и его расчет производится по приведенным выше формулам,

при сжатая зона элемента должна быть усилена постановкой дополнительной сжатой арматуры.