2. Характеристика трубопровода

В гидравлических расчетах простых и сложных трубопроводов используют графические методы, которые во многих случаях облегчают решение задач. Эти методы основаны на графическом построении характеристик трубопроводов.

Характеристикой трубопровода называется график зависимости суммарных потерь напора в трубопроводе от расхода.

Для простого трубопровода потери равны требуемому напору, который в общем случае может быть найден по формуле

(2.1)

,

которая при заданных значениях l, d, ∑ζ_i, К_э однозначно отражает зависимость напора Н от расхода Q.

Д

(2.2)

ля квадратной области зависимость (2.1) переходит в следующую

h_W = H = KQ² ,

а если учитывать только сопротивления по длине, то (2.2) примет вид

h

(2.3)

_W = H = A · l · Q²

Зависимости (2.1) и (2.2) возможно представить в координатах H – Q, задавая ряд значений Q и определяя соответствующие им значения Н.

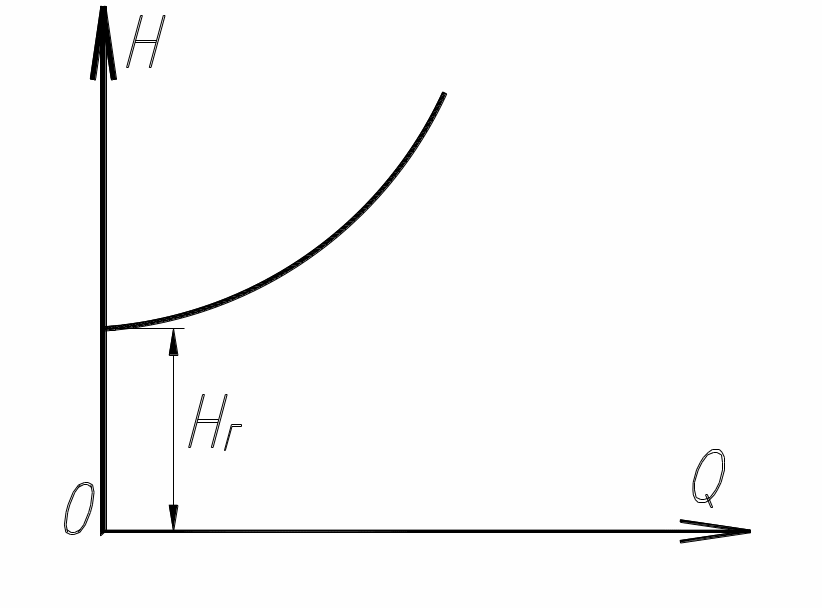
Рис.2.1

Рис. 2.2

Полученная на рис. 2.1 кривая представляет геометрический образ характеристики трубопровода. Если помимо гидравлических сопротивлений необходимо еще преодолеть геометрический напор Н_г (высоту Н_г или эквивалентную разность давлений), то график (характеристика трубопровода) будет иметь вид как на рис. 2.2 (Н = Н_г при Q=0).

П

ример. Рассмотрим расчет параллельного соединения простых трубопроводов в общем случае, когда заранее неизвестны зоны сопротивления в ветвях. Допустим, что имеются три ветви (число их на ход расчета не влияет).

Заданы: общий расход и параметры каждой из ветвей. Необходимо найти потери напора и расход в каждой из них.

Д

Рис. 2.3

ля решения задачи строим на одном графике в координатах H – Q характеристики всех ветвей, рис. 2.3 (в общем случае все они будут разные). Затем строим результирующую характеристику по нескольким точкам. Для этого при некотором значении Н, одинаковом для всех характеристик суммируем расходы и получаем точку для построения результирующей характеристики. После того, как она построена по нескольким точкам, откладываем на оси Q заданный суммарный (общий) расход, находим искомое значение Н и по каждой из характеристик ветвей находим значения расходов Q₁, Q₂ и Q₃.

Задача 2.1. Построить характеристику трубопровода, по которому при ламинарном режиме жидкость перетекает из одного резервуара в другой при постоянной разности уровней Н (принять, что местные потери отсутствуют и давление на свободной поверхности резервуаров атмосферное).

Указание Учесть выражение для λ при ламинарном режиме в формуле

.

3. Последовательное и параллельное соединение простых трубопроводов Последовательное соединение

Рассмотрим систему из последовательно соединенных труб различных диаметров и длин. Такое соединение участков трубопровода называется последовательным, рис. 3.1. А В

Рис.3.1. Рис.3.2.

О

(3.1)

чевидно, что расход во всех последовательно соединенных трубах один и тот же, а полные потери напора Н для всего трубопровода равны сумме потерь напора на всех участках, т.е.

Q

(3.2)

₁ = Q₂ = Q₃ = …= Q_n = Q

H = H₁ + H₂ + H₃ + …+ H_n,

где H₁, H₂ , H₃, …, H_n – потери напора на 1, 2, 3, …n-ом участке.

Учитывая, что для каждого участка последовательного соединения справедлива зависимость (1.7) и имея в виду, что на каждом участке расход одинаковый, запишем (3.2) в виде:

(3.3)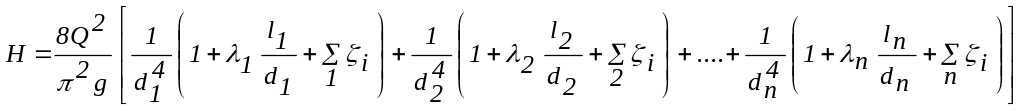

.

Из (4.3) следует, что решение первой и второй задач при последовательном соединении участков трубопровода разного диаметра будет таким же как для простого трубопровода (трубопровода постоянного диаметра).

Третья же задача, если в ней потребовать определения диаметров для всех участков, становится неопределенной, так как в этом случае уравнение (3.3) содержит n неизвестных. Для решения этой задачи необходимо задать диаметры труб для всех участков, кроме одного, который может быть тогда определен.

Задача 3.1. Определить потери напора в стальном трубопроводе, состоящем из двух участков длиной l₁ = 120 м и l₂ = 250 м. Диаметры труб участков d₁ = 120 мм и d₂ = 100 мм. Расход воды в трубопроводе Q = 12,2 л/с, кинематический коэффициент вязкости воды принять равным  = 0,01 см²/с.

Решение. В данном случае общие потери равны сумме потерь на каждом из участков. По справочнику определяем к_Э = 0,02 мм.

Определяем последовательно для первого участка

V₁ = = 1,1 м/с; Re₁ = 129511; Re₁ = 10,7; ₁ = 0,017;

Аналогично для второго участка

V₂ = 1,55 м/с; Re₂ = 155414; Re₂ = 31; ₂ = 0,017;

; h₁ + h₂ = 6.23 м.

Ответ: общие потери напора равны 6,23 м.