
- •1. Три задачи по расчету простого трубопровода
- •1.1 Классификация трубопроводов
- •1.2. Уравнение для расчета простого трубопровода
- •1.3 Три задачи по расчету простого трубопровода
- •2. Характеристика трубопровода
- •3. Последовательное и параллельное соединение простых трубопроводов Последовательное соединение
- •Параллельное соединение
- •4. Движение жидкости в трубах и каналах некруглого сечения
- •Для расчетов трубопроводов некруглого сечения применяют понятие эквивалентного диаметра, равного учетверенному значению гидравлического радиуса
- •5. Трубопроводы с насосной подачей жидкости
- •6. Основные законы равновесия и движения газов. Термодинамические свойства газов.
- •Основные уравнения для потоков газа.
- •Уравнение Бернулли для потоков газа.
- •7. Физические особенности работы газопроводов и каналов систем вентиляции. Газопроводы, работающие при малых перепадах давления.
- •Воздухопроводы систем вентиляции.
- •Изменение параметров газа вдоль трубы (газопроводы, работающие при больших перепадах давления)
- •8. Истечение жидкости через отверстия и насадки
- •Истечение через малое отверстие в тонкой стенке
- •8.2 Истечение при переменном напоре
- •Истечение через насадки при постоянном напоре
- •Внешний цилиндрический насадок
- •9. Основы теории пограничного слоя. Обтекание тел потоком жидкости и газа.
- •9.1. Понятие пограничного слоя и его свойства.
- •9.2. Расчёт сопротивления пластинки в потоке при продольном её обтекании
- •10. Обтекание тел потоком вязкой жидкости Отрыв пограничного слоя при обтекании криволинейных поверхностей.
- •Обтекание цилиндра потоком вязкой жидкости
- •11. Силы, действующие на обтекаемые потоком тела. Сила сопротивления трения и сила сопротивления давления.
- •Хорошо обтекаемые и плохо обтекаемые тела.
- •Определение сил, действующих на тела при обтекании их потоком жидкости.
- •Обтекание шара при малых числах Рейнольдса.
- •Определение вязкости жидкости с помощью формулы Стокса.
- •12. Гидродинамическое моделирование
- •Математическое, аналоговое и физическое моделирование
- •Геометрическое, кинематическое и динамическое подобие
- •3. Критерии гидродинамического подобия
- •Подобие потоков в случае преобладающего влияния сил тяжести
- •Подобие потоков в случае преобладания сил трения
- •Подобие потоков в случае преобладающего влияния сжимаемости жидкости
- •Подобие потоков в случае преобладающего влияния сил давления в этом случае условие частичного динамического подобия имеет вид
- •Подобие в случае одновременного действия нескольких сил
- •Автомодельность
- •Задачи.
- •Литература
Автомодельность
Если какая либо – величина, характеризующая гидравлическое явление не зависит от от какого – либо критерия подобия, то говорят, что она автомодельна по отношению к этому критерию. Например, коэффициент гидравлического сопротивления λ в квадратичной области и коэффициент Шези С не зависят от числа Рейнольдса и поэтому автомодельны по числу Re. При скорости течения газа не превышающих нескольких десятков метров в секунду сжимаемость можно не учитывать и такие течения мохно считать автомодельными по числу Маха. Существование областей автомодельности облегчает моделирование гидравлических явлений, так как делает ненужным удовлетворять некоторым критериям подобия.
Задача 12.6 Водосливная плотина в
виде водослива практического профиля
изучается в лаборатории на геометрически
подобной модели, выполняемой в масштабе
1:25. Определить: 1. Напор
![]() над верхней частью пластины на модели,
если в натуре он будет равен 4,5м;
над верхней частью пластины на модели,
если в натуре он будет равен 4,5м;
2. Расход через плотину в натуре,
если расход, полученный при испытании
модели, равен
![]()
Решение: Так как коэффициент геометрического подобия по условию задачи равен 25, то напор равен
![]()
Так как движение
через плотину происходит под действием
силы тяжести, то моделирование необходимо
производить по числу Фруда (вязкость
воды можно не учитывать), поэтому
![]() и
и
![]() и
и
![]() .
.
Кроме того,
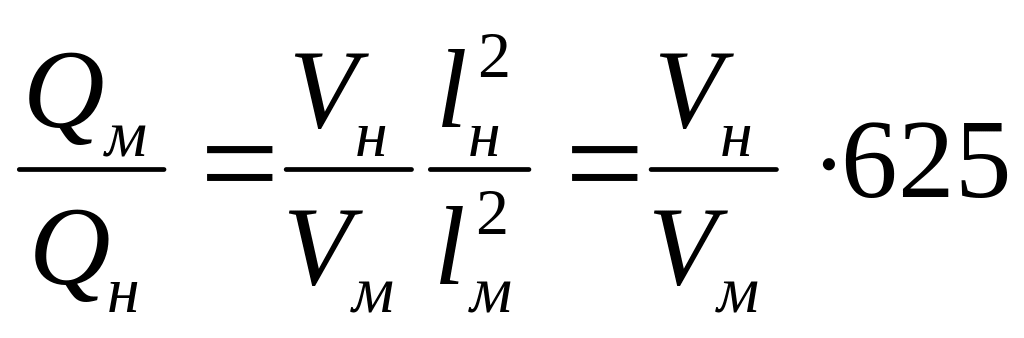 .
.
Окончательно
![]()
Задача 12.7. Масло
прокачивается в трубе диаметром
,
расход его равен Q.
Необходимо определить расход воды в
модельной установке- трубе диаметром
при условии, что движение в обеих трубах
должно быть гидродинамически подобным.
Коэффициенты кинематической вязкости
масла и воды равны соответственно
![]()
№ Варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Диаметр,
|
200 |
180 |
220 |
190 |
200 |
180 |
200 |
220 |
210 |
230 |
Расход, Q, л/с |
30 |
25 |
30 |
38 |
40 |
32 |
35 |
45 |
30 |
45 |
Диаметр,
|
100 |
85 |
120 |
110 |
110 |
85 |
85 |
100 |
89 |
120 |
№ Варианта |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Диаметр,
|
180 |
220 |
230 |
220 |
180 |
220 |
210 |
200 |
190 |
180 |
Расход, Q, л/с |
45 |
35 |
38 |
40 |
38 |
25 |
26 |
24 |
23 |
22 |
Диаметр,
|
110 |
120 |
89 |
70 |
75 |
100 |
80 |
70 |
50 |
80 |
№ Варианта |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Диаметр,
|
170 |
160 |
150 |
140 |
130 |
120 |
100 |
110 |
120 |
100 |
Расход, Q, л/с |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
Диаметр,
|
90 |
50 |
80 |
70 |
60 |
65 |
50 |
45 |
60 |
50 |
Задача 12.8. С
помощью моделирования необходимо
установить максимальное заглубление
![]() всасывающей трубы насоса под уровнем
нефти в резервуаре с тем, чтобы не
возникало воронки и не происходило
засасывание воздуха.
всасывающей трубы насоса под уровнем
нефти в резервуаре с тем, чтобы не
возникало воронки и не происходило
засасывание воздуха.
Насос в натурной установке откачивает расход нефти Q, по трубе диаметром . Испытания производятся на геометрически подобной модели, линейный масштаб которой принят равным 1:n от натуры.
Так как условия входа нефти в трубу определяется в данном случае совместным влиянием свойств инертности, вязкости и весомости жидкости, при моделировании необходимо соблюдать равенство чисел Ренольдса и Фруда. В задаче требуется определить:
Какова должна быть вязкость
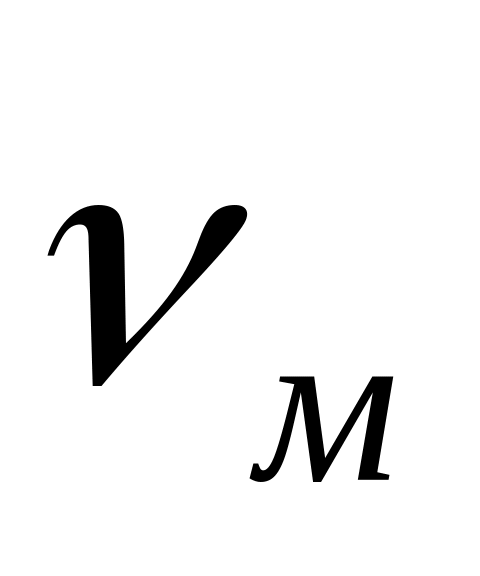 жидкости, используемой на модели.
жидкости, используемой на модели.Каков должен быть для модели откачиваемый расход
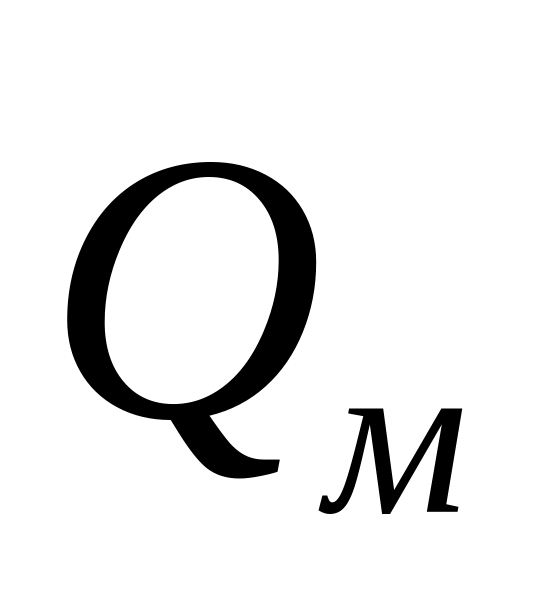 и какая будет при этом скорость
и какая будет при этом скорость
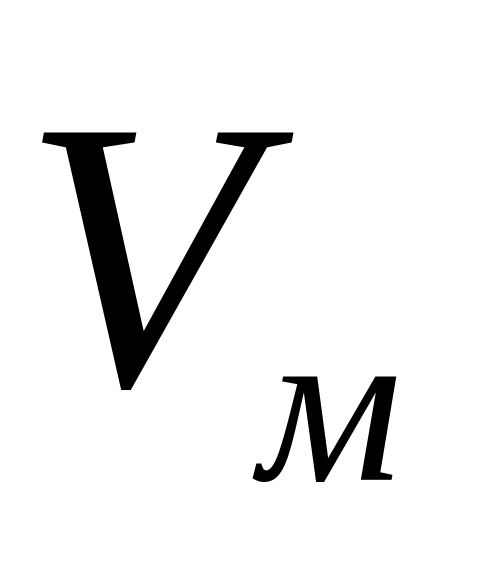 в трубе.
в трубе.При какой глубине начнет образовываться воронка на натурной установке, если для модели эта величина оказалась равной
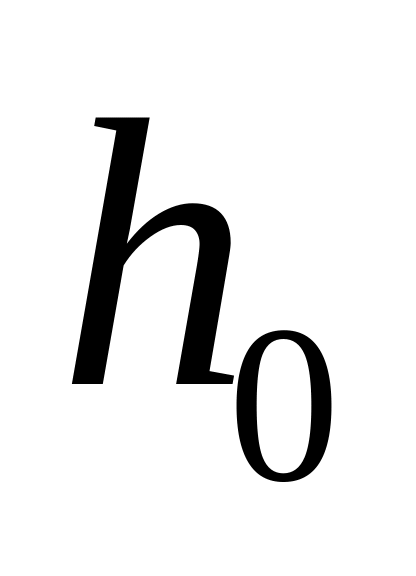 .
.
Принять кинематический
коэффициент вязкости нефти равным
![]() .
В качестве модельной жидкости можно
принять раствор глицерина в воде,
меняющий вязкость от
до
.
В качестве модельной жидкости можно
принять раствор глицерина в воде,
меняющий вязкость от
до
![]() в зависимости от соотношения глицерина
и воды.
в зависимости от соотношения глицерина
и воды.
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Расход,
|
140 |
150 |
130 |
120 |
110 |
100 |
120 |
130 |
110 |
100 |
Диаметр,
|
250 |
260 |
200 |
200 |
120 |
200 |
150 |
250 |
200 |
240 |
Коэффициент Подобия, n |
5 |
6 |
4 |
8 |
4 |
4 |
5 |
6 |
3 |
4 |
Глубина,
|
60 |
70 |
80 |
90 |
100 |
90 |
80 |
70 |
90 |
80 |
№ варианта |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Расход,
|
90 |
80 |
70 |
60 |
50 |
110 |
120 |
130 |
140 |
110 |
Диаметр,
|
200 |
100 |
89 |
50 |
100 |
200 |
220 |
230 |
240 |
190 |
Коэффициент Подобия, n |
5 |
3 |
4 |
5 |
4 |
5 |
6 |
5 |
6 |
4 |
Глубина,
|
70 |
60 |
90 |
80 |
100 |
60 |
70 |
80 |
90 |
100 |
№ варианта |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Расход,
|
120 |
130 |
140 |
110 |
120 |
130 |
140 |
100 |
110 |
120 |
Диаметр,
|
200 |
210 |
220 |
240 |
160 |
170 |
160 |
170 |
160 |
170 |
Коэффициент Подобия, n |
5 |
6 |
4 |
5 |
6 |
4 |
5 |
6 |
4 |
5 |
Глубина,
|
110 |
100 |
90 |
80 |
70 |
60 |
56 |
90 |
70 |
80 |
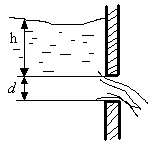
Задача 12.9.
Истечение
керосина (![]() )
через отверстие диаметром d
моделируется на воде (
)
при соблюдении вязкого и гравитационного
подобия.
)
через отверстие диаметром d
моделируется на воде (
)
при соблюдении вязкого и гравитационного
подобия.
Определить:
Диаметр отверстия
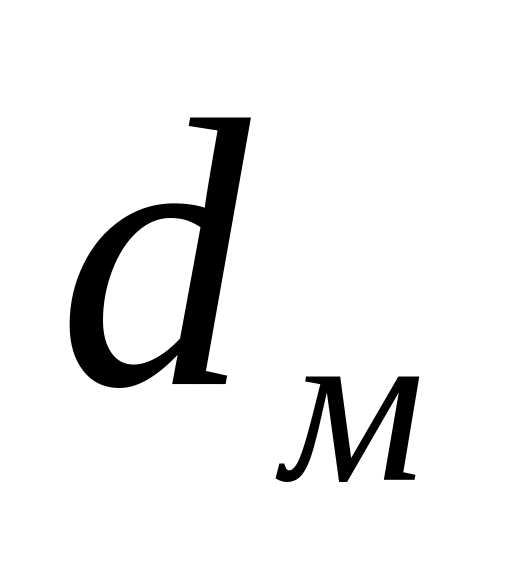 для модели
для моделиВ каком отношении должны находиться высоты уравнений для натуры
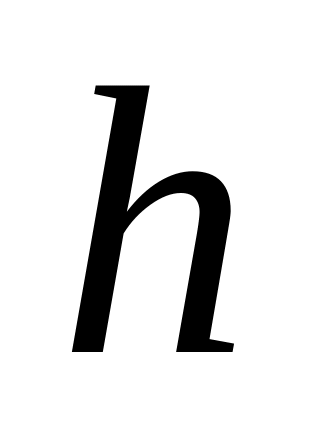 и для модели
и для модели
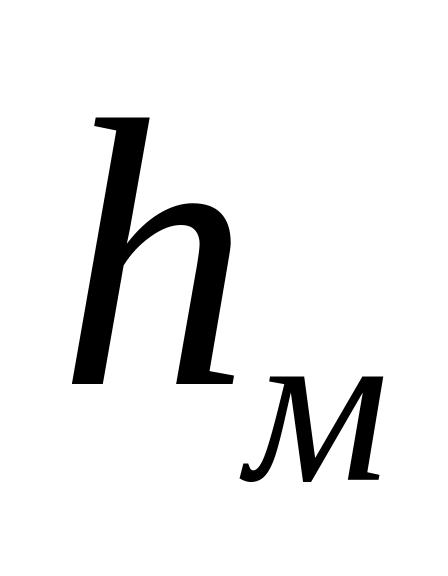 .
.В каком отношении при выполнении этих условий будут находиться расходы Q и
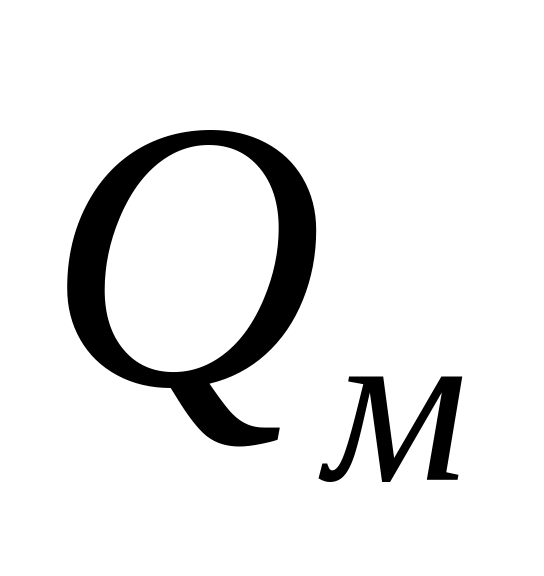 .
.
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Диаметр,
|
80 |
75 |
85 |
76 |
54 |
68 |
96 |
94 |
84 |
80 |
№ варианта |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
Диаметр,
|
82 |
78 |
94 |
88 |
90 |
80 |
70 |
