11. Силы, действующие на обтекаемые потоком тела. Сила сопротивления трения и сила сопротивления давления.

На тело, помещённое в поток жидкости, последний оказывает воздействие, мерой которого является сила гидродинамического воздействия; она может быть разложена на две составляющих. Одна из них определяется нормальными напряжениями (т.е. давлением), действующими на поверхности обтекаемого тела, а вторая – касательными напряжениями. Другими словами сила гидродинамического воздействия может быть разложена на силу, обусловленную давлением, действующим на поверхности тела и силу, обусловленную трением между жидкостью и телом. В гидродинамике принято рассматривать проекции составляющих силы гидродинамического воздействия на направление скорости набегающего потока и называть их силой сопротивления давления и силой сопротивления трения. Сумма данных сил (т.е. проекция силы гидродинамического воздействия на направление скорости набегающего потока) называется силой лобового сопротивления.

Поясним сказанное на примере обтекания потоком тонкой пластинки. При этом здесь и далее, для определённости, договоримся рассматривать только установившиеся движение жидкости. Если пластинка установлена вдоль потока, рис. 11.1, то, пренебрегая толщиной пластины, можно считать, что сила воздействия потока представляет собой силу трения между слоем жидкости, примыкающим к пластине, и её поверхностью. Другими словами в «чистом» виде наблюдается сила сопротивления трения, а сила сопротивления давления в данном случае равна нулю (так как вдоль поверхности пластины сверху и снизу будут возникать касательные напряжения , а нормальные напряжения на верхней и нижней поверхности пластинки компенсируют друг друга).

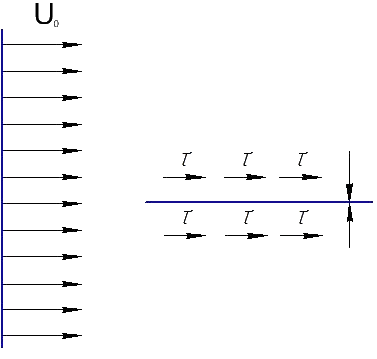
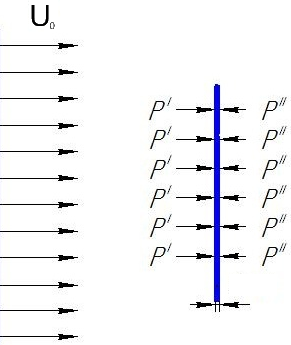
Рис. 11.1. Рис. 11.2.

Если пластинка установлена поперек потока, рис. 11.2., возникает обратная картина; на передней и задней поверхности пластины будут возникать нормальные напряжения (давления), а касательные напряжения , можно считать нулевыми. На поверхности пластины (на передней и задней сторонах) если и существуют касательные напряжения, то направлены они строго вдоль пластины и в проекции на направление потока дают ноль. В данном случае наблюдается в «чистом» виде сила сопротивления давления. Если пластина будет располагаться под некоторым углом к набегающему потоку, будут возникать как сила сопротивления давления, так и сила сопротивления трения.

Силу сопротивления трения принято вычислять по формуле

(11.1)

где – коэффициент сопротивления трения; – плотность жидкости, – площадь обтекаемой поверхности тела; – скорость набегающего потока.

Коэффициент сопротивления трения в общем случае зависит от числа Рейнольдса и шероховатости обтекаемой поверхности тела.

Силу сопротивления давления находят по формуле

, (11.2)

где – коэффициент сопротивления давления; – плотность жидкости, – площадь миделевого сечения тела; – скорость набегающего потока.

Под площадью миделевого сечения тела понимают наибольшую площадь проекции обтекаемого тела на плоскость, перпендикулярную направлению движения потока.

Коэффициент сопротивления давления в общем случае зависит от числа Рейнольдса, формы тела и ориентации тела по отношению к потоку обтекаемой поверхности тела. Если форма тела и его ориентация в потоке жестко заданы, то коэффициент сопротивления давления зависит только от числа Рейнольдса.

Силу лобового сопротивления, учитывая сказанное выше, находят как

. (11.3)

Задача 11.1. Два металлических шара одинакового радиуса, но с различными массами соединены нитью. При помещении в жидкость система этих шаров тонет; в случае, когда она в жидкости предоставлена самой себе, через некоторое время движение её становится равномерным. Определить, при каком соотношении между массами шаров сила натяжения нити равна весу более легкого шара. Какие условия необходимо наложить на длину нити для коррективного решения задачи?

Решение. Если бы шары не были связаны, то скорость падения более тяжелого шара была бы больше; поэтому при любых начальных условиях соединяющая шары нить после установления движения расположится вертикально так, что более тяжелый шар окажется внизу. Все действующие на шары силы – силы сопротивления, натяжения нити, силы тяжести и выталкивающие силы – направлены по вертикали.

Условие равномерного движения верхнего шара имеет вид

,

аналогично для нижнего шара

,

где – целое число. Вычитая из второго уравнения первое находим значение и отношение масс шаров, которое должно быть равно 1:3.