8.2 Истечение при переменном напоре

Рассмотрим истечение из резервуара через отверстие без поступление в него жидкости извне. Этот процесс будет нестационарным – глубина жидкости в резервуаре (напор) будет изменяться.

Поставим задачу - определить время, в течении которого уровень жидкости резервуаре изменится на заданную величину.

Если скорость изменения уровня мала, то возможность применить уравнение Бернулли для установившегося движения и использовать зависимость для расхода Q при истечении, полученную выше.

Обозначим переменную высоту уровня жидкости в сосуде, отсчитываемую от дна, через h, площадь сечения резервуара на этом уравне S(h), а площадь отверстия S_o, рис.8.3.

Рис 8.3.

За бесконечно малый интервал времени dt уровень в резервуаре понизится на величину dh и вытекший объём dw будет равен dw=S.dh. С другой стороны, через отверстие за время dt вытечет тот же самый объём dw, равный dw=Q.dt, где . Т (8.8) аким образом S.dh=-Q.dt или

знак минус в (8.8) обусловлен тем, что положительному приращению dt соответствует отрицательное приращение dh (с увеличением времени уровень в резервуаре понижается).

Из (8.8) можно определить время изменения уровня от Н₁ до Н₂

(8.9)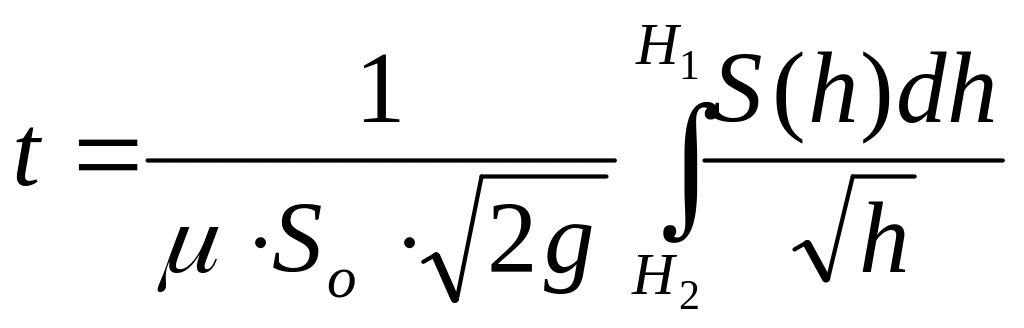

.

Хотя коэффициент расхода μ может зависеть от скорости истечения (а следовательно от h), его приближённо принимают постоянным.

Входящий в (8.9) интеграл может быть в случае резервуара произвольного сечения подсчитан одним из способов приближённого интегрирования.

Если S=const, то интеграл в (8.9) может быть подсчитан аналитически

.

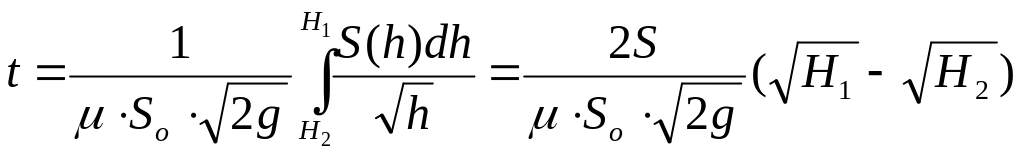Время полного опорожнения резервуара (Н₂=0) равно .

Задача 8.3 Круглый призматический резервуар высотой Н заполнен доверху водой. При открытии в его дне отверстия диаметром d он опорожняется полностью за время t₀. Как изменится время t₀ при одновременном

1. Уменьшение высоты Н в 4 раза;

2. Уменьшение диаметра отверстия d в 2 раза.

3. Истечение через насадки при постоянном напоре

На практике часто бывает необходимо увеличить коэффициент расхода, добиться сохранения формы струи (гидромонитор, брандспойт) и т.п. Для этой цели в технике применяют различные насадки.

Насадкой называется короткая труба, присоединённая к отверстию в тонкой стенке.

Обычно длина насадка, заключена в пределах от 3d до 5d, где d – диаметр отверстия, равный внутреннему диаметру насадка. Насадки влияют на коэффициенты скорости и сжатия струи, а тем самым на величину коэффициента расхода .

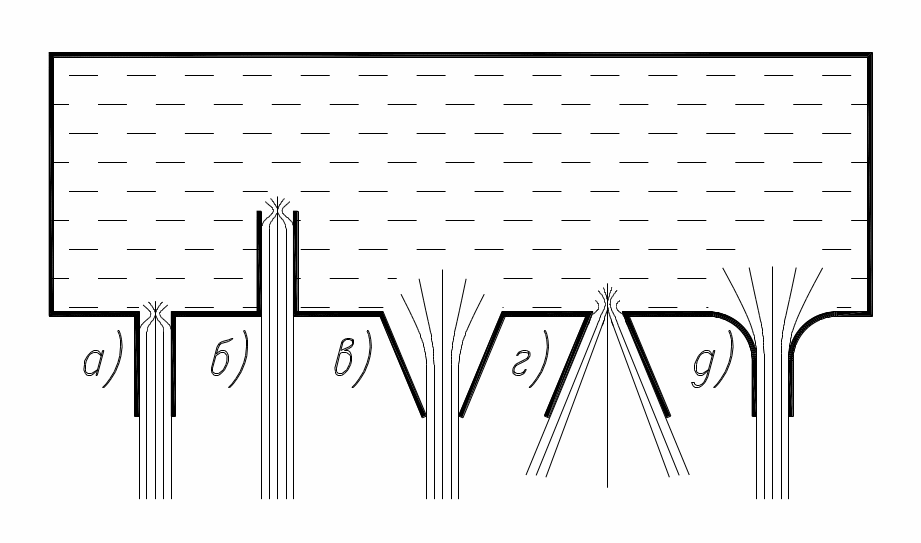
Рис.8.4.

По своей форме насадки бывают цилиндрические внешние, рис.8.4.а (μ=0,82), цилиндрические внутренние, рис. 8.4.б (μ=0,71), конически сходящиеся, рис. 8.4.в (μ=0,92), конические расходящиеся, рис. 8.4.г (μ=0,57), и коноидальные рис. 8.4.д (μ=0,97).

Расчетные формулы для определения расхода через насадки при постоянном напоре такие же, как для отверстия в тонкой стенке, а именно

(8.10)

где μ – коэффициент расхода, величина которого зависит от вида насадки.

Задача 8.4 Определить утечку воды из тепловой сети через образовавшееся в результате аварии отверстие в стенке трубопровода. Избыточное давление в сети р_изб=4ат, температура воды 95^оС (ρ=960 кг/м³), площадь отверстия S=1см². коэффициент расхода μ=1.

Решение В данном случае размеры отверстия (щели) соизмеримы с толщиной стенок трубы, поэтому истечение нужно представлять как истечение через насадок. Массовый расход воды, кг/с, через образовавшиеся отверстие определяется по формуле

где Q – объёмный расход, м³/с, ΔН – напор в м. вод. столба м. водн. ст. кг/с.