
- •1. Три задачи по расчету простого трубопровода
- •1.1 Классификация трубопроводов
- •1.2. Уравнение для расчета простого трубопровода
- •1.3 Три задачи по расчету простого трубопровода
- •2. Характеристика трубопровода
- •3. Последовательное и параллельное соединение простых трубопроводов Последовательное соединение
- •Параллельное соединение
- •4. Движение жидкости в трубах и каналах некруглого сечения
- •Для расчетов трубопроводов некруглого сечения применяют понятие эквивалентного диаметра, равного учетверенному значению гидравлического радиуса
- •5. Трубопроводы с насосной подачей жидкости
- •6. Основные законы равновесия и движения газов. Термодинамические свойства газов.
- •Основные уравнения для потоков газа.
- •Уравнение Бернулли для потоков газа.
- •7. Физические особенности работы газопроводов и каналов систем вентиляции. Газопроводы, работающие при малых перепадах давления.
- •Воздухопроводы систем вентиляции.
- •Изменение параметров газа вдоль трубы (газопроводы, работающие при больших перепадах давления)
- •8. Истечение жидкости через отверстия и насадки
- •Истечение через малое отверстие в тонкой стенке
- •8.2 Истечение при переменном напоре
- •Истечение через насадки при постоянном напоре
- •Внешний цилиндрический насадок
- •9. Основы теории пограничного слоя. Обтекание тел потоком жидкости и газа.
- •9.1. Понятие пограничного слоя и его свойства.
- •9.2. Расчёт сопротивления пластинки в потоке при продольном её обтекании
- •10. Обтекание тел потоком вязкой жидкости Отрыв пограничного слоя при обтекании криволинейных поверхностей.
- •Обтекание цилиндра потоком вязкой жидкости
- •11. Силы, действующие на обтекаемые потоком тела. Сила сопротивления трения и сила сопротивления давления.
- •Хорошо обтекаемые и плохо обтекаемые тела.
- •Определение сил, действующих на тела при обтекании их потоком жидкости.
- •Обтекание шара при малых числах Рейнольдса.
- •Определение вязкости жидкости с помощью формулы Стокса.
- •12. Гидродинамическое моделирование
- •Математическое, аналоговое и физическое моделирование
- •Геометрическое, кинематическое и динамическое подобие
- •3. Критерии гидродинамического подобия
- •Подобие потоков в случае преобладающего влияния сил тяжести
- •Подобие потоков в случае преобладания сил трения
- •Подобие потоков в случае преобладающего влияния сжимаемости жидкости
- •Подобие потоков в случае преобладающего влияния сил давления в этом случае условие частичного динамического подобия имеет вид
- •Подобие в случае одновременного действия нескольких сил
- •Автомодельность
- •Задачи.
- •Литература
8. Истечение жидкости через отверстия и насадки
Истечение через малое отверстие в тонкой стенке
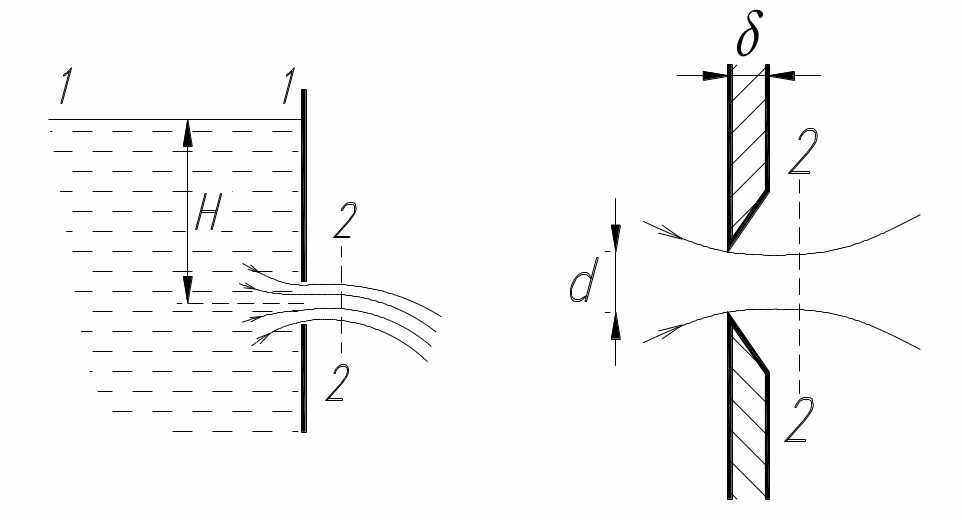
Рассмотрим истечение жидкости из резервуара через малое отверстие, рис.8.1. Глубина погружения центра отверстия под свободной поверхностью равна Н; часто величина Н называется напором. Истечение происходит при постоянном напоре; это возможно, если в резервуар подаётся такой же расход, какой вытекает из отверстия. Задача состоит в определении скорости и расхода потока жидкости вытекающей из отверстия. Предварительно дадим несколько определений.
Рис8.1. |
Малым отверстием называется такое, у которого наибольший вертикальный размер d не превышает 0,1Н ( d ≤ 0,1Н ). Траектории частиц жидкости при приближении к отверстию искривляются и за сечением отверстия в свободной струе образует сжатое сечение, рис.8.1.б. |
Ближайшее к отверстию сечение струи, в котором движение может быть принято плавно изменяющемся, находится на расстоянии примерно 0.5d от внутренней поверхности стенки резервуара; оно называется сжатым сечением. Стенку можно считать тонкой, если её толщина δ никак не влияет на процесс истечения; в частности полагают, что δ<0,2d , d – диаметр отверстия, через которое жидкость вытекает.
Коэффициентом сжатия ε называется отношение площади сжатого сечения Sc к площади отверстия S
(8.1.)![]()
Для решения задачи применим уравнение Бернулли для потока вязкой жидкости к сечениям, движение в которых плавно изменяющееся; такими сечениями является – свободная поверхность в резервуаре 1-1 и сжатое сечение струи 2-2, рис.8.1.а. Потери в данном случае происходят за счёт искривления струек и выражаются зависимостью
(8.2)![]()
где V
– скорость в сжатом сечении, ξ –
коэффициент местных сопротивлений. Из
рис.8.1. следует: р1=р2=рат,
V1=0,
V2≡Vc,
z1-z2=H,
поэтому уравнение Бернулли (![]() )
принимает вид
)
принимает вид
(8.3)![]()
окончательно получаем для скорости
(8.4)![]()
где величина φ
(8.5)![]()
н
(8.6)
![]()
Расход при истечении (с учётом (8.1) и (8.6))
![]()
и
(8.7)
![]()
Произведение
![]() называется
коэффициентом расхода.
называется
коэффициентом расхода.
Если известны значения ε,φ,S и Н, то возможно найти скорость и расход при истечении; таким образом поставленная задача решена.
При расчёте истечения через отверстие возможны три типа задач:
Определение расхода Q при известных напоре Н и площади отверстия Sо.
Определение напора Н, необходимого для пропуска заданного расхода Q через отверстие площади Sо.
Определение площади отверстия Sо при известных Q и H.
Для обычных условий истечения значения основных коэффициентов полагают такими: μ=0,60-0,62; φ=0,97; ε=0,61-0,64; ξ=0,06.
Задача 8.1 Круглое отверстие диаметром d=15мм в стенке открытой бочки с водой закрыто пробкой. Глубина над центром отверстия равна Н=0,85м. Определить скорость и расход воды, вытекающий из отверстия сразу же после удаления пробки. Принять μ=0,60; φ=0,97.
Решение Все расчёты выполним в
системе СИ, поэтому g=9,81м/с.
Скорость истечения определяем по формуле
(8.6) V=0,97.![]() .
Площадь отверстия равна
.
Площадь отверстия равна
![]() .
Расход определяется по зависимости (8.
7) Q=0.6.0.00018.
.
Расход определяется по зависимости (8.
7) Q=0.6.0.00018.![]() .
.
|
Задача 8.2 Истечение жидкости начинает происходить в некоторый момент времени из закрытого резервуара 1 в большую ёмкость 2, давление газа в которой постоянно и равно р2, рис8.2. Давление газа над свободной поверхностью жидкости в сосуде 1 равно р1, высота столба жидкости Н. рассмотреть два случая истечения: в первом плотность жидкости ρ1 во втором ρ2, ρ2> ρ1 (например вода и ртуть). В остальном все условия истечения одинаковы. Определить, в нашем случае скорость в начальный момент больше. Сделать анализ решения. |

 +
а) б)
+
а) б)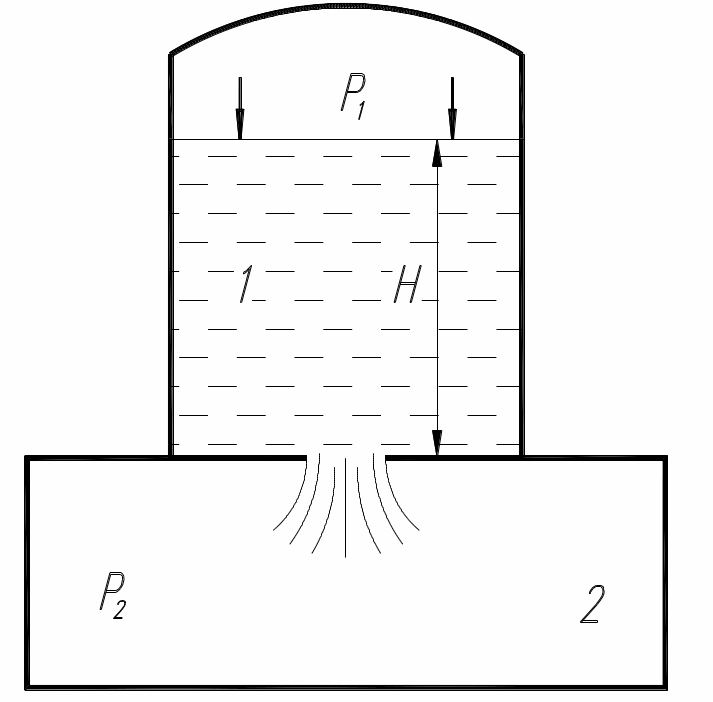 Рис 8.2
Рис 8.2