Гидравлика

_______________________________________________________________________________________________________________________________________________________________________________________________________________

Калякин А.М.

Спецкурс по гидравлике

(для студентов специальности ТГС)

Учебное пособие

2010

Введение

Цель настоящего пособия- дать углубленные знания по гидравлике и аэродинамике студентам специальности ТГС (после изучения ими общего курса гидравлики).

На законах гидравлики основан расчет разнообразных гидротехнических сооружений, трубопроводов для подачи различных жидкостей, а также других гидравлических устройств.

Аэродинамикой называется наука, изучающая движение газообразных сред, а также взаимодействие их с твердыми телами и поверхностями.

На законах аэродинамики основаны расчеты летательных аппаратов, трубопроводов, транспортирующих различные газы (воздухопроводов, газопроводов, паропроводов), конструирование газовых машин (турбин, компрессоров, вентиляторов), проектирование котельных агрегатов, печных и сушильных установок и т.д.

Знание законов механики жидкости необходимо для решения многих технических вопросов в области санитарной техники, в частности водоснабжения, водоотведения, теплогазоснабжения и вентиляции. Кроме того, гидравлика и аэродинамика служат теоретической базой при изучении ряда специальных дисциплин.

Пособие состоит из нескольких частей, в каждой из которых изложена определенная тема (темы независимы друг от друга). В пособие также включены задачи, решение которых обязательно.

Для студентов дневной формы обучения номера задач и варианты условий задает преподаватель.

Для студентов заочной формы обучения алгоритм выбора заданий такой:

1. Вторая и третья задачи по расчету простого трубопровода, стр. 7 и стр. 9, и задачи 3.2, стр.16: студент решает тот вариант этих задач, который совпадает с последними двумя цифрами его зачетной книжки.

2. Если последняя цифра номера зачетной книжки четная (ноль «0» считается четным числом, а единица «1»- нечетным), то студент решает следующие задачи

4.2; 8.5; 12.7

Если Последняя цифра номера зачетной книжки нечетная, то студент решает задачи

7.3; 8.7; 12.8

Номер варианта (от 1 до 10) в условии каждой задачи берется по предпоследней цифре номера зачетной книжки.

Пример. Номер зачетной книжки студента-заочника заканчивается цифрами 32.

Студент должен решить:

1. Вторую и третью задачи и задачу 3.2 под номером варианта 32.

2. Задачи 4.2; 8.5; 12.7 (выбрать вариант задания в условиях всех этих задач под номером 3)

1. Три задачи по расчету простого трубопровода

1.1 Классификация трубопроводов

Трубопроводы нашли исключительно широкое применение в водоснабжении, транспортировке нефти и газа, в системах теплоснабжения, в различных энергетических и двигательных установках.

Жидкость движется по трубопроводу вследствие того, что ее потенциальная энергия в начале трубопровода больше, чем в конце. Эта разность потенциальных энергий необходима для преодоления гидравлических сопротивлений между рассматриваемыми сечениями трубопровода. Она может быть создана разными способами: а) работой насоса; б) благодаря разности уровней жидкости – самотечная подача; в) из-за повышенного давления газа на свободную поверхность жидкости в баке – вытеснительная подача. При расчете трубопроводов используются: уравнение неразрывности, уравнение Бернулли, зависимости для расчета сопротивлений и экспериментальные данные.

Простыми трубопроводами называют такие, у которых диаметр трубы, а также расход жидкости на всем протяжении остаются неизменными, а сложными – все остальные. Любой сложный трубопровод всегда возможно представить состоящим из ряда простых.

1.2. Уравнение для расчета простого трубопровода

Простой трубопровод – это труба постоянного диаметра с местными сопротивлениями, по которой проходит постоянный расход.

Большинство простых трубопроводов вписывается в одну из следующих двух схем, рис. 1.1.; в резервуарах уровень поддерживается постоянным и поэтому течение везде установившееся.

Схема 1 Схема 2

Рис.1. 1.

В обоих случаях движущей силой является сила тяжести, которая приводит к разности давлений и под действием этой разности жидкость приходит в движение. В обоих случаях потенциальная энергия положения преобразуется в кинетическую энергию, а последняя – в тепловую за счет сил трения.

С точки зрения анализа размерностей очевидно, что на скорость течения V в трубе влияет разность уровней H, а так как движущей силой является сила тяжести, то оказывает влияние и ускорение свободного падения, т.е.

(1.1)

.

Точнее результат для скорости течения получается, если приравнять запас потенциальной энергии и кинетическую энергию текущей жидкости.

Для случая идеальной жидкости

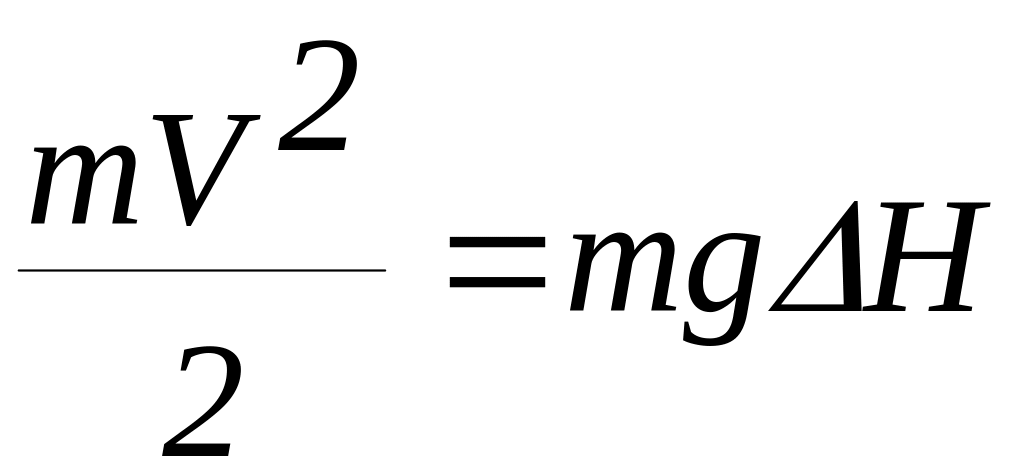или .

В действительности вследствие вязкости (трение в жидкости) часть кинетической энергии переходит в тепловую. Поэтому чем больше сопротивлений по длине и местных, тем скорость течения меньше.

Как это часто бывает, наиболее точный и исчерпывающий результат получается при решении общих уравнений. В данном случае вполне понятно, что основным уравнением, связывающим запас потенциальной энергии, кинетическую энергию потока и потери является уравнение Бернулли

(1.2)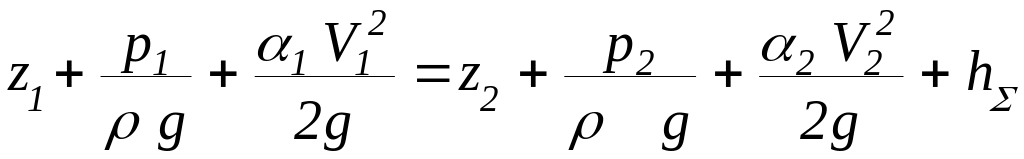

Суммарные потери h_Σ складываются из потерь по длине h_l и местных h_м

(1.3)

,

(1.4)

(1.5)

.

Выбираем плоскость (ось) сравнения, совпадающей с осью горизонтальной части трубопровода, а сечения 1-1 и 2-2 совпадающими со свободными поверхностями в сосудах, рис. 1.1.

Физический смысл уравнения для схемы 1 следующий: потенциальная энергия положения частично преобразуется в кинетическую энергию жидкости, вытекающей в атмосферу и частично превращается в тепло. Для схемы 2 имеем H=h_пот, т.е. вся потенциальная энергия полностью преобразуется в тепло.

Уравнения баланса энергии для обеих схем имеют одинаковый вид, а именно

(1.6)

В случае схемы 2 из всей суммы коэффициентов местных сопротивлений выделяется коэффициент внезапного расширения при входе трубы в емкость 2 (он равен единице, т.е.  = 1).

Если труба круглая, то (2.6) преобразуется к виду (V = 4Q/d²)

(1.7)

Это уравнение будем в дальнейшем называть уравнением для расчета простого трубопровода.

Задача 1.1. Вывести уравнение для расчета простого трубопровода при перетекании жидкости из одного закрытого резервуара в другой под действием силы тяжести и давления газа на поверхностях. Рассмотреть случаи:

а) перетекание из 1 в 2; б) перетекание из 2 в 1; в) жидкость покоится. Написать условия перетекания и сделать краткий анализ решения.