Предмет теории вероятности

Виды случайных событий

Случайным событием (просто событием) назы-вается любой факт, который в результате может произойти или не произойти.

Испытание – это выполнение определенного комплекса условий, в котором наблюдается то или иное явление, фиксируется тот или иной факт.

Обозначение: А,В,С и т.д.

Соб.А – выигрыш авто по билету лотереи

Соб.В – появление герба при подбрасывании монеты.

Два события А и В называются несовместными, если наступление одного исключает появление другого. (Пример: соб.А – студент получил 5 на экзамене, соб.В – этот же студент получил 4 по этому же предмету. Соб.А и В несовместные, т.к. не могут произойти при одном исходе испыта-ний.)

Два события А и В называются совместными, если они могут произойти при одном исходе испытаний. (Студент получил 5 по одному пред-мету и 4 по другому)

Событие называется достоверным, если в ре-зультате испытания оно обязательно должно произойти.

Событие называется невозможным, если в ре-зультате испытания оно вообще не может про-изойти. (Пример: в партии изделия все стандарт-ные. Соб.А – извлечение стандартного изделия, соб.В – извлечение брака. А – достоверное, В – невозможное)

События называются равновозможными, если в результате испытания по условиям симметрии не одно из этих событий не является объективно более возможным.(Пример: пусть происходит подбрасывание монеты. Соб.А- орел, соб.В – решка)

Несколько событий называются единственно возможными, если в результате испытания обя-зательно должно произойти хотя бы одно из них.

События образуют полную группу, если они являются единственно возможными и несовме-стными исходами испытания.

Два несовместных события, из которых одно должно произойти называются противополож-ными.

Обозначение: А,

Операции над событиями

1. Событие C называется суммой A+B, если оно состоит из всех элементарных событий, входящих как в A, так и в B. При этом если элементарное событие входит и в A, и в B, то в C оно входит один раз. В результате испытания событие C происходит тогда, когда произошло событие, которое входит или в A или в B. Сумма произвольного количества событий   состоит из всех элементарных событий, которые входят в одно из Ai, i=1, ..., m.

 

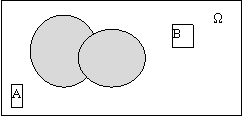
 2. Событие C произведением A и B, если оно состоит из всех элементарных событий, входящих и в A, и в B. Произведением произвольного числа событий   называется событие состоящее из элементарных событий, входящих во все Ai, i=1, ..., m.

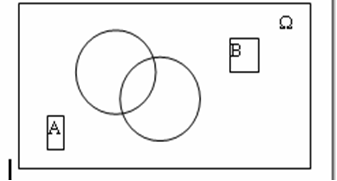
 3. Разностью событий A-B называется событие C, состоящее из всех элементарных событий, входящих в A, но не входящих в B.

 

 4. Событие   называется противоположным событию A, если оно удовлетворяет двум свойствам.

Формулы де Моргана:     и  

 

5. События A и B называются несовместными, если они никогда не могут произойти в результате одного испытания.

События A и B называются несовместными, если они не имеют общих элементарных событий.

C=AxB=V

Тут V - пустое множество.

Относительна частота и вероятность событий

Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов W(A)=m/n .

Замечание: отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

Пример 1. В коробке находится шары. Из коробки наугад извлекают 5 шаров и 2 из них оказались красными. Найти относительную частоту появления красного шара.

Решение:

Т.к. из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:

При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события, т.е.P(A)=lim W(A) .

Определение. Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий P(A)=m/n.

Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.

Очевидно, относительная частота и вероятность могут не совпадать.

Замечание. Вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

Классическое определение вероятности.

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Далее укажем слабые стороны этого определения и приведем другие определения, позволяющие преодолеть недостатки классического определения.

ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

ОБОЗНАЧЕНИЕ: 

Элементы комбинаторики.

Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой.

Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать k способами, а элемент Y можно выбрать n способами, то пару XYможно составить kn способами.

Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно  .

Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из k элементов (km), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из mэлементов по k элементов, а их общее число можно выразить формулой  .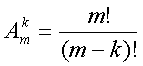

Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно: 

Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k  m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний из m элементов по k элементов вычисляется по формуле: 

Теорема сложения вероятностей. (для попарно несовместимых событий)

  Пусть A, B, C — попарно несовместимые события и m_A , m_B , m_C — соответственно числа их появлении в n испытаниях. Тогда событие A + B + C появится m_A + m_B + m_C раз при этих n испытаниях и, следовательно, частость события A + B + C будет равна сумме частостей событии A, B, C, так как

Поэтому и для средних значений этих частостей (когда производится несколько серий испытаний), или, другими словами, для вероятностей, следует положить

P ( A + B + C ) = P ( A ) + P ( B ) + P ( C )

т. е. имеет место   Теорема сложения вероятностей (для попарно несовместимых событий). Вероятность того, что произойдет одно из попарно несовместимых событий, равна сумме вероятностей этих событий.   Следует особо подчеркнуть, что здесь речь идет о попарно несовместимых событиях. В противном случае данная формула не будет справедлива, так как при совместимости событий нельзя утверждать, что событие A + B + C появится m_A + m_B + m_C  раз.  

P ( A₁ + A₂ + ... + A_m ) = P ( A₁ ) + P ( A₂ ) + ... + P ( A_m )

   Так как P ( D ) = 1, то из предидущего равенства для полной системы событий получаем

P ( A₁ ) + P ( A₂ ) + ... + P ( A_n ) = 1

(события A₁ , A₂ , ... , A_n по определению попарно несовместимы), В частности, для противоположных событий имеем

P ( A ) + P (   ) = 1

Теорема умножения вероятностей

Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)РА(В).

В частности, для независимых событий

Р(АВ) = Р(А)Р(В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предложении, что все предыдущие события уже наступили:

Р (А1А2А3 ... Аn)=P(A1)*PA1(А2)PA1A2(A3)...PA1A2...An-1(Аn),

где PA1A2...An-1(Аn)—вероятность события Аn, вычисленная в предположении, что события A1, А2, .... An-i наступили.

В частности, вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероят¬ностей этих событий:

Р (А1А2 ... Аn) = Р (А1)*Р(А2) ... Р (Аn).

Независимые события

Два события A и B называются независимыми, если P(A/B)=P(A); P(B)=P(B/A) - доказать.

В этом случае вероятность наступления двух событий A и B равна P(AB)=P(B)P(A/B)=P(A)P(B),

при этом покажем, что P(B/A)=P(B); P(AB)=P(B)P(A)=P(A)P(B/A)

События A1A2...Ak называются независимыми между собой, если вероятность их совместного наступления  ;  . Два независимых события совместны.

* Если бы события были несовместны, то P(A/B)=0 и P(B/A)=0, т.к. они независимы, то P(A/B)=P(A) и P(B/A)=P(B), т.е. утверждение “независимые события несовместны”, т.к. P(A)=0 и P(B)=0, то это утверждение неверно.

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Пусть дано вероятностное пространство  , и полная группа попарно несовместных событий  , таких что            . Пусть   — интересующее нас событие. Тогда

.