21.. Методы анализа динамических систем с непрерывным временем. Общая методика анализа динамических систем

Для однорідних ланцюгів керуючі потоки є найпростішими, а імовірності переходів - постійними, причому передбачається, що , так як немає необхідності вважати переходами ті ситуації, коли ланцюг залишається в колишньому стані. Переходи зі стану в стан можна зв'язати з появою подій найпростішого потоку, одержуваного "просіванням" (розрідженням) керуючого потоку стану . Найпростіший потік характеризується єдиним параметром - інтенсивністю (відповідно до виразу (4.6)).

Якщо випадковий процес, що протікає в системі з дискретними станами і безупинним часом, є марківським, то для ймовірностей станів технічної системи ( ), які находяться по графу функціонування системи можна скласти систему лінійних диференціальних рівнянь Колмогорова, Кількість таких рівнянь дорівнює числу можливих станів системи, їхня сукупність утворить систему спільних диференціальних рівнянь. Щоб вирішити рівняння Колмогорова й знайти ймовірності станів, необхідно задати початкові умови, наприклад, виду [6]

Граф функціонування системи та система диференціальних рівнянь Колмогорова є складовими частинами математичної моделі надійності технічної системи.

Методика включає наступні етапи.

1. Аналіз системи і визначення множини станів .

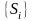2. Побудова розміченого графа переходів.

3. Одержання системи рівнянь Колмогорова.

4. Вирішення системи рівнянь Колмогорова.

5. Аналіз знайдених ймовірностей

6. Розробка рекомендацій щодо поліпшення характеристик системи.

22. Типовые структуры динамических систем

Структуру блукання добре ілюструє процес «загибелі та розмноження». Процес «загибелі та розмноження». Безперервний марківський ланцюг називається процесом «загибелі та розмноження», якщо його граф станів представляє ланцюг (рис. 4.12), у якому кожний із середніх станів (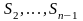 ) пов'язаний прямим і зворотним зв'язком з кожним із сусідніх станів, а крайні стани ( ) – тільки з одним сусіднім станом [1, 5].

Система лінійних диференціальних рівнянь Колмогорова при цьому має вигляд

Неважко помітити, що даний ланцюг ергодичний, всі стани в ньому сполучені, а значить у стаціонарному режимі система диференціальних рівнянь вироджується в систему лінійних алгебраїчних рівнянь

при виконанні умови нормування (4.1), тобто .

. (4.18)

Отже, всі ймовірності виражені через одну з них , значення якої можна одержати, використовуючи нормувальну умову (4.1)

. (4.19)

Циклічний процес. Безперервний марківський ланцюг називається циклічним процесом, якщо стани зв'язані між собою в кільце (цикл) з однобічними переходами (рис. 4.13) [1].