19.. Общие подходы к анализу динамических систем
Функціонування
багатьох технічних систем являє собою
послідовність переходів з одного стану
в інший. При такому формалізованому
уявленні процесу функціонування системи
вивчення її характеристик зводиться
до вивчення абстрактного процесу
переходів з одного стану в інший в межах
повної множини станів. Нехай
є деяка технічна система
,
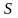що у процесі функціонування може приймати
різні стані
(
).
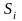Причому система перебуває
в деякому стані
,
якщо вона повністю описується значеннями
змінних, які задають цей стан, тобто
відповідно до виразу (1.2) стан
визначає величина:
,
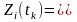де
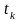- момент часу;
- випадкова величина, що характеризує
стан системи в момент часу
,
(
)
- властивість системи, що описує поточний
стан,
- кількість властивостей системи,
необхідних для визначення стану
. Система
робить
перехід
з одного стану в інший, якщо значення
змінних
,
що задають цей стан, поміняються на
інші, що задають інший стан. Якщо стані
системи змінюються в часі випадковим
образом, то їхню послідовність можна
розглядати як випадковий процес, тобто
сімейство випадкових величин {
}
(
)
утворює випадковий (стохастичний) процес
[1, 2]. Якщо множина станів системи численна,
їхня зміна характеризується поступовими,
плавними переходами зі стану в стан, то
процес, що протікає в системі, є випадковим
процесом з безперервними
станами.
Система називається системою з
дискретними станами,
якщо множина її станів рахуєма (або
скінчена), а переходи з одного стану в
інший здійснюються стрибком. Послідовність
станів такої системи, тобто випадковий
процес переходів зі стану в стан
називається ланцюгом. Марківськімоделі
є могутнім інструментом представлення
та дослідження складних технічних
систем. Це зумовлено, наступними причинами
[1, 3]:
вони знайшли широке застосування серед сучасних методів дослідження складних технічних систем, тому що є узагальненням математичної моделі системи з незалежно працюючими елементами;
вони відносно прості і доступні широкому класу дослідників і, водночас, дозволяють враховувати залежність стану системи від її попереднього стану, що дуже важливо для динамічних систем;
використання марківських моделей дозволяє пояснити фізичний зміст процесів, що протікають у технічній системи.
20.
метод анализа динамических систем с
дискретным временем Процес,
що володіє марківською властивістю й
описує систему з кінцевим числом станів
(
),
переходи в якому здійснюються у фіксовані
моменти часу, називається дискретним
марківським ланцюгом.
При цьому кожному переходу відповідає
перехідна ймовірність
.
Для кожного моменту часу переходи
утворюють повну групу подій [1, 3]
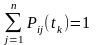, (4.3)
де
відповідно до виразу (4.2)
.
Взаємозв’язок
між перехідними ймовірностями
та ймовірностями станів
(ймовірностями того, що в момент часу
система знаходиться в стані
)
показано на рис. 4.2
Графічну модель можливих станів такої системи можна умовно зобразити у вигляді орієнтованого графа станів. На такому графі кожному стану системи ставиться у відповідність вершина графа, що з'єднується ребрами з іншими вершинами. Напрямки ребер відповідають напрямкам можливих переходів, а імовірності переходів розглядаються як ваги відповідних ребер [3, 4].