7.1.3 Свертывание критериев

В рассмотренных выше методах степень важности трех критериев была принята одинаковой. Это означает, что используемые в качестве критериев ключевые параметры эффективности NPV, NPI и Т_ок, для инвестора одинаково важны_. Однако, чаще всего инвестор, решая свои задачи, неодинаково оценивает степень важности этих критериев. Например, в одном случае для инвестора самым важным параметром является срок окупаемости проекта, в другом чистый дисконтированный доход, в третьем индекс доходности, в четвертом – внутренняя норма доходности. В таких случаях при расчете сравнительной эффективности проектов вводятся коэффициенты важности критериев. После этого коэффициенты весомости нормируются и используются в расчетах выбора оптимального варианта. Поясним эту процедуру на конкретном примере.

Предположим, что лица, принимающие решения, оценили степень важности критериев рассмотренного выше примера по пятибалльной шкале и присвоили им следующие коэффициенты весомости A_i:

	NPV, млн руб.	NPI	Ток, годы
Ai	5	2	1

Для проведения дальнейших операций присвоенные коэффициенты весомости необходимо нормировать, для чего применим простой способ нормирования по формуле:

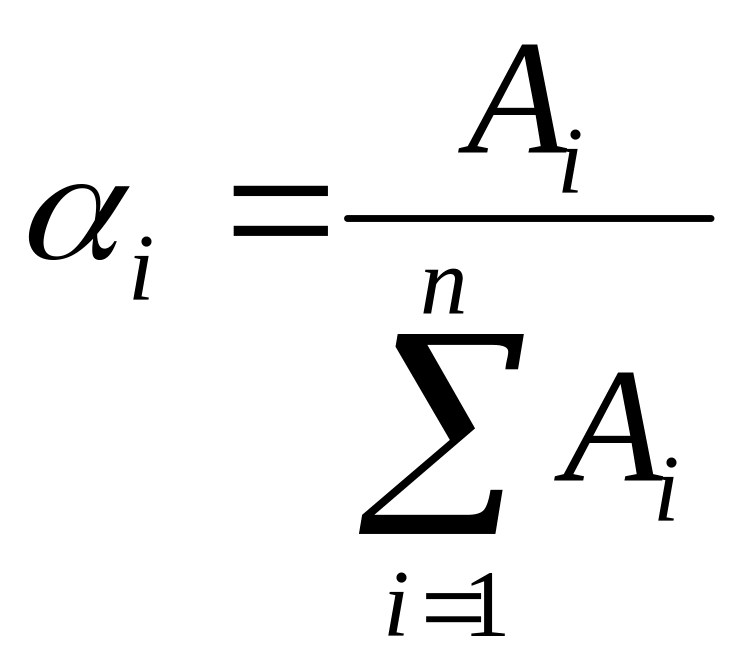, (7.8)

где - нормированный коэффициент весомости.

	NPV, млн руб.	NPI	Ток, годы
Ai	5	2	1
	5/(5+2+1) = 0,62	0,25	0,13

Очевидно, что и >0

Теперь применим метод свертывания критериев, который позволяет произвести выбор оптимального варианта проекта с учетом степени важности сравниваемых критериев по следующей формуле:

(7.9)

Произведем расчет по этой формуле, воспользовавшись данными таблицы 7.4, и запишем результаты в таблицу 7.7.

Таблица 7.7 Результаты расчета методом свертывания критериев.

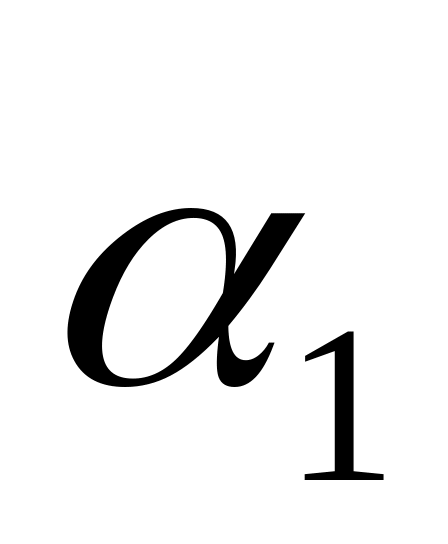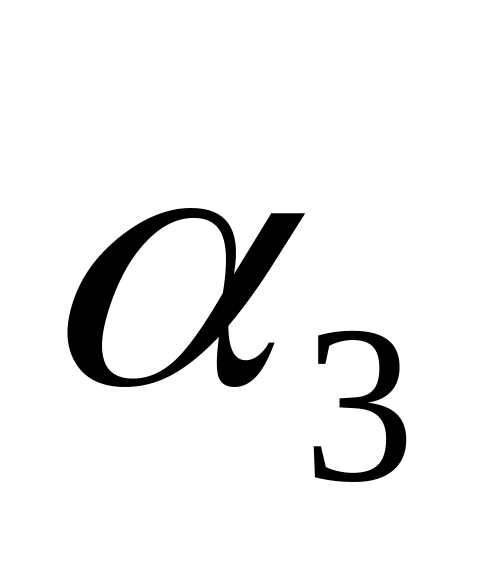Номер варианта j	f1j	f2j	f3j	Суммарное значение fj(x)
1	2	3	4	5
1	0	0,025	-0,037	-0,01
2	0,56*0,29=0,18	0,05	-0,085	0,15
3	0,27	0,25	0	0,52
4	0,45	0,075	-0,13	0,4
5	0,62	0	-0,09	0,53

Из полученных нами результатов следует, что экономически наиболее эффективным оказался пятый вариант инвестиционного проекта. Таким образом, с помощью предыдущих методов наилучшим был выбран вариант №3, а сейчас - вариант №5. В чем причина получения разных результатов оценки? Ответить на этот вопрос нетрудно: при использовании метода равномерной оптимизации и метода отклонения от идеальной точки мы предположили, что степень важности сравниваемых критериев одинакова. Однако, если их степень важности различна с точки зрения экспертов, то и оптимальный вариант может быть другим, что и произошло в нашем примере при использовании метода свертывания критериев, который позволяет учитывать весомость критериев.

Таким образом, эффективность проекта следует оценивать, применяя несколько критериев одновременно и учитывая степень их важности для инвестора.