Глава 7. Методика выбора оптимального варианта инвестиционного проекта.

7.1. Понятие многоцелевой оптимизации и методы ее применения

Остановимся на проблеме применения основных оценочных показателей эффективности при осуществлении выбора среди нескольких альтернативных вариантов проекта, для которых эти показатели определены, одного, наиболее результативного. Сложность ситуации заключается в том, что одни показатели лучше у одной части вариантов проекта, другие - у другой. Очевидно, что оценка экономической эффективности по каждому в отдельности из этих показателей может привести к неверным результатам. В этой связи возникают вопрос, как учесть одновременно все показатели и какой из вариантов проектов будет оптимальным? Решение этой задачи носит многокритериальный (многоцелевой) характер. Воспользуемся методикой выбора экономически целесообразного проекта из нескольких альтернативных, подробно рассмотренной В.В. Царевым в книге «Оценка экономической эффективности инвестиций» [27], основанной на базе применения методов многоцелевой оптимизации.

В соответствии с этой методикой первоначально необходимо задаться показателями эффективности (критериями), по которым будут оцениваться варианты проекта и производиться выбор лучшего из них. В качестве критериев выбираются все или некоторые (в зависимости от характера проекта) оценочные показатели эффективности. Остановимся, к примеру, на следующих: чистый дисконтированный доход (NPV), индекс доходности(NPI), дисконтированный срок окупаемости (Т_ок).

С целью сравнения вариантов построим матрицу, для элементов которой введем следующие обозначения:

x_j - альтернативные варианты проекта, подлежащие сравнению, где:

j – номер варианта (j= 1, …m);

X_j - оптимальный вариант проекта;

f_i(x) – значение показателя эффективности, где i – номер показателя (i =1, ...n)

Зададимся номерами i. Пусть NPV соответствует номер i =1, NPI - i =2, Т_ок - i=3.

Задача заключается в выборе из множества альтернативных проектов x_j оптимального варианта X_j.

С точки зрения показателя чистого дисконтированного дохода, как известно, наиболее эффективным является тот проект, у которого NPV максимален. То же самое относится к индексу доходности дисконтированных инвестиций NPI. И, наоборот, показатель дисконтированного срока окупаемости Т_ок должен быть минимальным. Это рассуждение может быть записано в формализованном виде с помощью целевых функций:

f₁(x) , (7.1)

f₂(x) , (7.2)

f₃(x) (7.3)

Формула (7.1) отражает требование максимизации чистого дисконтированного дохода, формула (7.2) отражает требование максимизации индекса доходности, формула (7.3) отражает требование обеспечения минимального срока окупаемости.

Поставленная задача требует одновременного выполнения условий трех целевых функций. Для решения такого рода задач применяются методы многоцелевой оптимизации.

Рассмотрим пример, в котором имеются 5 альтернативных инвестиционных проектов, из которых необходимо выбрать наиболее эффективный.

Для каждого проекта были рассчитаны величины NPV, NPI и Т_ок, и результаты расчетов сведены в таблицу 7.1.

Номер варианта j	NPV, млн руб.	NPI	Ток, годы
1	2	3	4
1	18	1,18	3,5
2	20	1,19	4,0
3	21	1,27	3,1
4	23	1,21	4,5
5	25	1,17	4,1

Таблица 7.1 Показатели эффективности для пяти вариантов проекта.

Как видно, при сравнении вариантов по критерию NPV лучшим является вариант №5, по критерию индекса доходности NPI – лучший вариант №3, по критерию срока окупаемости Т_ок – наиболее оптимальный вариант №3. Попробуем учесть все рассматриваемые критерии и определить оптимальный вариант.

Поскольку критерии эффективности характеризуют разные экономические показатели и соответственно они имеют разные единицы измерения, то первым шагом при выполнении поставленной задачи является процедура их нормализации. Она представляет собой приведение показателей к безразмерным величинам и производится по формуле:

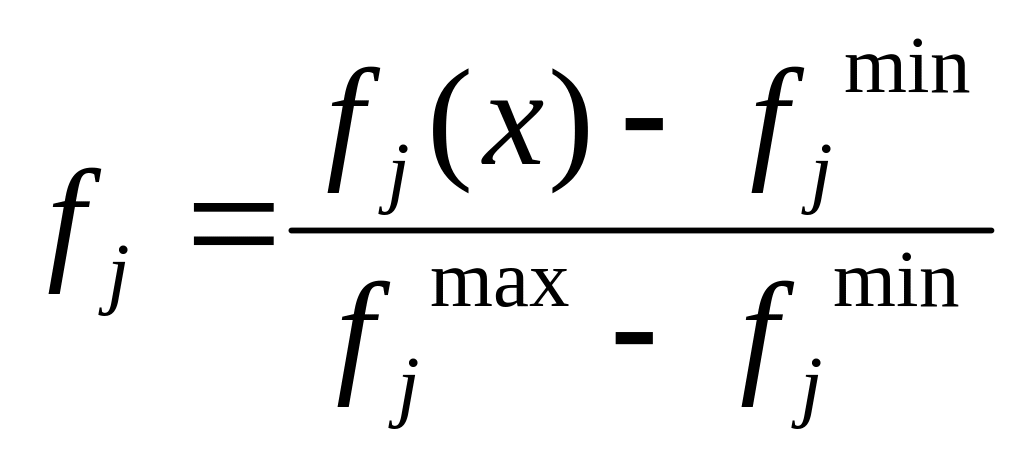, где (7.4)

f_j – нормализованное значение рассматриваемого j-того критерия;

и – максимальное и минимальное соответственно значения

j-того критерия;

f_j(x)- текущее значение j-того критерия.

Например, для первого варианта имеем:

f_1,1 =(18-18)/(25-18)=0

f_1,2 =(1,18-1,17)/(1,27-1,17)=0,1

f_1,3 =(3,5-3,1)/(4,5-3.1)=0.29

Таким же образом рассчитаем все варианты проектов, и результаты представим в таблице 7.2.

Номер варианта j	f1j	f2j	f3j
1	2	3	4
1	0	0,1	0,29
2	0,29	0,2	0,65
3	0,43	1	0
4	0,72	0,3	1
5	1	0	0,72

Таблица 7.2 Нормализованные значения показателей эффективности

для пяти вариантов проекта.

В связи с тем, что целевые функции рассматриваемых параметров разнонаправлены (7.1; 7,2; 7,3), первоначально необходимо выполнить процедуру, которая позволит привести все целевые функции в одно направление. В нашем случае целевые функции от NPV и NPI стремятся к максимуму, а целевая функция от Ток – к минимуму. С целью обеспечения единого направления целевых функций, что является необходимым условием при проведении выбора вариантов математическими методами, изменим направление целевой функции от Ток, умножив данные f_3j (четвертого столбца табл.7.3.) на (-1). Тогда эта целевая функция тоже будет стремиться к максимальному значению.

Номер варианта j	f1j	f2j	f3j
1	2	3	4
1	0	0,1	-0,29
2	0,29	0,2	-0,65
3	0,43	1	0
4	0,72	0,3	-1
5	1	0	-0,72

Таблица 7.3 Формирование единого направления целевых функций.

Теперь, когда параметры нормализованы и их целевые функции приняли одно направление, рассмотрим некоторые несложные математические методы, позволяющие определить наиболее эффективный вариант проекта.