6.5. Внутренняя норма доходности

Как отмечалось выше, значение чистого дисконтированного дохода зависит от нормы дисконта Е, которая определяет доход, приемлемый для инвестора. Эта зависимость представлена на графике (РИС. 6.1).

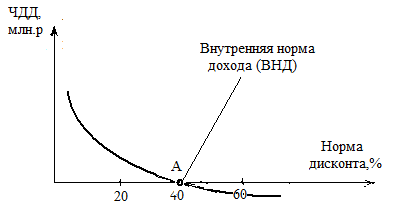
РИС. 6.1. График изменения ЧДД в зависимости от нормы дисконта Е.

Следует отметить, что подобная зависимость чистого дисконтированного дохода от нормы дисконта справедлива для таких проектов, в которых все инвестиционные затраты осуществляются в начале жизненного цикла, а спустя определенное время начинаются денежные поступления, в результате которых значения накопленного дисконтированного дохода из отрицательных величин переходят в положительные.

Характер зависимости ЧДД от нормы дисконта Е монотонно убывающий: с ростом последней величина чистого дисконтированного дохода падает, достигая нулевого значения в точке Е₀, а затем приобретает отрицательные значения. Точка Е₀, в которой ЧДД становится равным нулю, определяет ту норму дисконта, при которой дисконтированное значение инвестиционных оттоков равно дисконтированному значению притоков от реализации проекта. С точки зрения оценки эффективности инвестиционных проектов норма дисконта в этой точке является весьма важным показателем, отражающим размер дохода в расчете на единицу вложенных инвестиций. Этот показатель носит название внутренней нормы доходности проекта (ВНД), помимо этого используются синонимы: внутренняя норма прибыли, внутренняя норма рентабельности, Internal Rate of Return (IRR).

Таким образом, внутренняя норма доходности отражает такой уровень доходности инвестиционного проекта, при котором происходит полное покрытие всех расходов по проекту доходами от его реализации, то есть полная окупаемость инвестиций.

Математически это представлено следующей формулой:

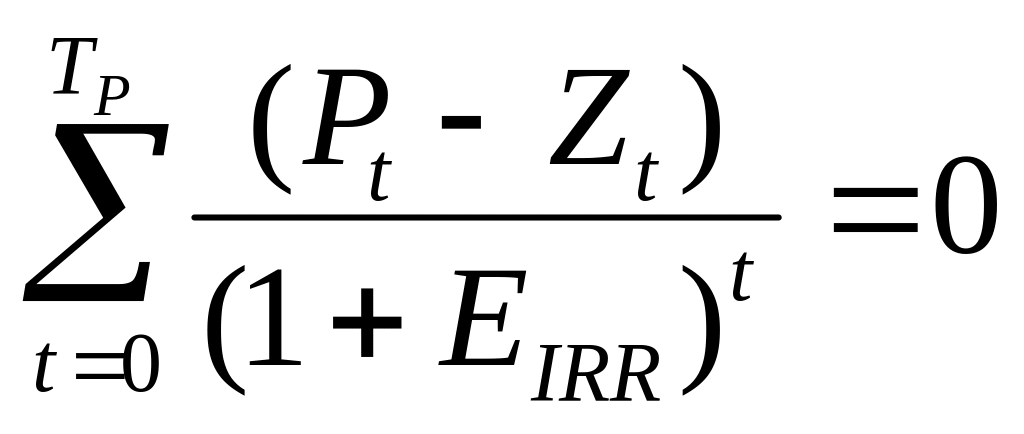, (6.7)

где: P_t - притоки по проекту на шаге t;

Z_t – оттоки по проекту на шаге t;

Е_IRR – величина внутренней нормы доходности.

Если в результате решения этого уравнения значение Е_IRR превысит значение нормы дисконта, то реализация проекта признается целесообразной, поскольку в этом случае он принесет доход, больше минимально приемлемого уровня, установленного инвестором с помощью параметра Е.

Если значение Е_IRR меньше нормы дисконта, то проект отклоняется. Если же Е_IRR равен норме дисконта, то проект не принесет прибыли, но и не станет убыточным.

При ознакомлении с понятием внутренней нормы доходности часто возникает вопрос, в чем состоит принципиальное отличие показателей Е и Е_IRR? Ответ заключается в том, что норму дисконтирования Е инвестор определяет, исходя из собственного понимания приемлемого уровня дохода на свои денежные вложения. Инвестора интересует такой уровень прибыли, который обеспечит, по меньшей мере, минимально приемлемый для него доход, компенсацию потерь от инфляции и от инвестиционных рисков. В отличие от нормы дисконтирования, величина внутренней нормы доходности Е_IRR формируется на основе объективных данных, генерируемых проектом - значений затрат и поступлений.

Пример 6.7.

Величина внутренней нормы доходности проекта составила - 26%. Принимая решение на предынвестиционной фазе о вложении денег, инвестор определил минимально допустимую норму дохода - 6%, потери от инфляции – 10%, потери от возможных рисков – 7%.

Суммарная норма дисконтирования Е в соответствии с формулой (4.13) составила: (0,06+0,1+0,06*0,1+0,07)*100%= 23,6%. Получив прибыль от проекта с внутренней нормой доходности, равной 26%, инвестор направит на компенсацию потерь от инфляции и от рисков - 17%. У него останется: 26% - 17%=9% (а не 6%, как планировалось). Кроме того, если рисковое событие не наступит, то потери 7% не произойдет, а, следовательно, реальный доход возрастет на 9+7=16%.

Остановимся на методике определения значения Е_IRR из уравнения (6.6), величина которого может быть найдена лишь приближенно с заданной степенью точности. Одним из путей решения этого уравнения относительно Е_IRR является применение метода половинного деления, представляющего собой итерационный процесс, обеспечивающий последовательное приближение к искомому результату.

Поясним алгоритм применения этого метода на практике, для чего вновь обратимся к графику изменения чистого дисконтированного дохода в зависимости от нормы дисконтирования Е (РИС.6.1). Наша задача - найти такое значение нормы дисконтирования Е₀, при котором NPV обращается в нуль. Для этого необходимо совершить ряд последовательных шагов – итераций, которые постепенно приведут к искомому результату. Первоначально, задаваясь различными значениями Е, следует найти такое значение Е₁, при котором NPV > 0, и такое значение Е₂, при котором NPV < 0. В этом случае на отрезке (Е₁; Е₂) значение NPV меняет знак, а, следовательно, в какой-то точке Е₀ значение NPV становится равным нулю. Затем произведем половинное деление, то есть отрезок (Е₁; Е₂) разделим пополам и обозначим точку деления Е₃. Определим значение NPV в точке Е₃, после чего из двух отрезков (Е₁; Е₃) и (Е₃; Е₂) выберем тот, на концах которого NPV имеет разные знаки. Предположим, это отрезок (Е₁; Е₃). Таким образом мы сузили границы поиска Е₀ в два раза. Продолжим последовательные приближения. Разделим отрезок (Е₁; Е₃) пополам, точку деления обозначим как Е₄ и вновь определим значение NPV в этой точке. Далее, опять из образовавшихся двух выберем отрезок, на концах которого NPV имеет разные знаки. Процесс половинного деления продолжается до тех пор, пока расчетное значение NPV не приблизится с определенной заданной степенью точности к нулю. Значение Е, при котором это произойдет, и будет искомым Е₀. Остается добавить, что подобные многоступенчатые расчеты производят с применением компьютерных программ.

Пример 6.8.

Рассчитать внутреннюю норму доходности инвестиционного проекта, имеющего сальдо денежных потоков по годам расчетного периода, представленные в таблице 6.5, Окупаемость проекта должна произойти на третьем году расчетного периода.

Расчет произвести с точностью вычисления нулевого значения NPV до трех знаков после запятой.

	Годы расчетного периода
	0	1	2	3
Сальдо денежных потоков, млн руб.	-20	8	10	10

Таблица 6.5 Денежные потоки инвестиционного проекта.

Для расчета внутренней нормы доходности воспользуемся формулой (6.6), в которой чистый дисконтированный доход равен нулю (NPV=0):

.

Подставим в формулу имеющиеся данные и будем вычислять NPV, подбирая величину Е методом половинного деления, до тех пор, пока NPV не примет значения нуля с заданной точностью (до третьего знака после запятой):

Данный метод предполагает проведение нескольких шагов расчета до момента достижения необходимой точности.

1 шаг. Сначала зададимся нормой дисконтирования Е=0,1 и определим с помощью программы EXCEL чистый дисконтированный доход: NPV=3,05 (Таблица 6.6.) Обозначим эту точку на оси Е Точкой 1.

2 шаг. Теперь попробуем «нащупать» отрицательное значение NPV. Зададимся достаточно большой величиной Е=0,3 и рассчитаем NPV. Оно равно: NPV= - 3,377. Обозначим эту точку Точкой 2

Это означает, что искомая точка Е₀, обращающая NPV в ноль, находится внутри этого интервала.

3 шаг. Интервал {1;2} разделим на два, точку деления обозначим Точкой 3 и определим Е=(0,1+0,3)/2=0,2.

Для Е=0,2 вычислим. NPV=-0,602. Поскольку результат отрицательный, то для дальнейшего рассмотрения выбираем интервал {1;3}, на концах которого NPV имеет разные знаки.

Последующие шаги. Делим выбранный интервал пополам, обозначаем Точкой 4 и продолжаем итерационный процесс до двенадцатого шага, на котором NPV приобретает нулевое значение с точностью до третьего знака после запятой, что соответствует условию задачи. Найденная величина внутренней нормы доходности в данном примере:

Е_IRR = 0,181

№ точки	Место точки на оси Е	E	NPV
1	Точка 1	0,1000	3,050
2	Точка 2	0,3000	-3,377
3	Середина интервала { 1;2}	0,2000	-0,602
4	Середина интервала {1;3}	0,1500	1,093
5	Середина интервала {4;3}	0,1750	0,216
6	Середина интервала {5;3}	0,1875	-0,200
7	Середина интервала {5;6}	0,1813	0,006
8	Середина интервала {7;6}	0,1844	-0,097
9	Середина интервала {7;8}	0,1828	-0,046
10	Середина интервала {7;9}	0,1820	-0,020
11	Середина интервала {7;10}	0,1816	-0,007
12	Середина интервала {7;11}	0,1814	-0,0004

Таблица 6.6 Расчет внутренней нормы доходности.