
- •29. Теория функций комплексной
- •29.1. Основные понятия теории функций
- •I уровень
- •II уровень
- •III уровень
- •29.2. Функция комплексной переменной,
- •I уровень
- •II уровень
- •III уровень
- •29.4. Однозначные элементарные функции
- •1. Экспонента
- •2. Тригонометрические функции
- •3. Гиперболические функции
- •I уровень
- •II уровень
- •III уровень
- •29.7. Ряды на комплексной плоскости
- •I уровень
- •II уровень
- •III уровень
I уровень
1.1. Вычислите интеграл
 по прямолинейному отрезку, соединяющему
точки
и
по прямолинейному отрезку, соединяющему
точки
и
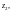 если:
если:
1)
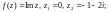 2)
2)
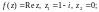
3)
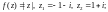 4)
4)
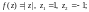
5)
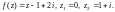
1.2. Вычислите интеграл
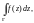 если Г представляет собой ломаную ABC,
состоящую из двух прямолинейных отрезков
AB и BC:
если Г представляет собой ломаную ABC,
состоящую из двух прямолинейных отрезков
AB и BC:
1)

2)
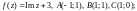
3)
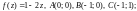
4)

II уровень
2.1. Вычислите интеграл если путь Г представляет собой ломаную ABC, состоящую из двух прямолинейных отрезков AB и BC:
1)
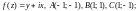
2)
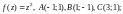
3)
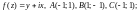
4)
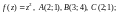
5)
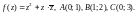
2.2. Вычислите интеграл
где Г – дуга указанной кривой от точки
до точки

1)
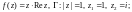
2)
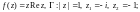
3) 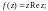 Г – парабола с вершиной в точке (1; 0),
проходящая через точку
Г – парабола с вершиной в точке (1; 0),
проходящая через точку
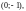
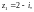
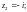
4)
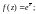
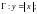
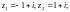
5)
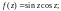
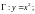
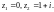
2.3. Вычислите интеграл
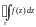 по указанной замкнутой кривой
по указанной замкнутой кривой
1)
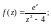
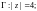 2)
2)
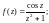
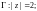
3)
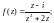
 4)
4)
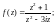
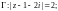
5)
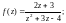
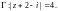
III уровень
3.1. Вычислите интеграл
по указанной замкнутой кривой Г (число
m – целое, т. е.
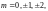 …):
…):
1)
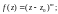
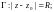
2)
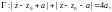

3)
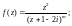
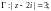
4)
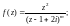
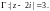
29.7. Ряды на комплексной плоскости
Пусть
– последовательность комплексных
чисел,
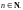
Выражение вида
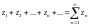
называется числовым рядом, числа
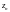 – элементами ряда, сумма
– элементами ряда, сумма
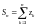 – n-й частичной
суммой ряда.
– n-й частичной
суммой ряда.
Если последовательность
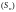 частичных сумм сходится, то ряд называется
сходящимся, ее предел
частичных сумм сходится, то ряд называется
сходящимся, ее предел
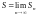 называется суммой ряда, что
записывают
называется суммой ряда, что
записывают
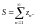
Если последовательность расходится, то ряд называется расходящимся. Расходящийся ряд суммы не имеет.
Величина
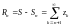
называется остатком сходящегося ряда. Из сходимости ряда следует равенство
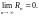
Если ряды
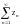 и
и
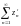
сходятся и имеют суммы соответственно
S и S,
то ряд
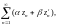
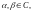 сходится к сумме
сходится к сумме
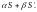
Ряд
 называется действительной частью
ряда
называется действительной частью
ряда
 а ряд
а ряд
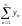 – мнимой частью ряда
– мнимой частью ряда
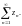
Ряд с комплексными элементами сходится тогда и только тогда, когда сходятся его действительная и мнимая части, причем в случае сходимости
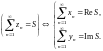
Необходимый признак сходимости:
если ряд с комплексными элементами
сходится, то
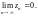
Достаточный признак расходимости:
если
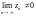 (или не существует), то ряд расходится.
(или не существует), то ряд расходится.
Ряд
называется абсолютно сходящимся,
если сходится ряд
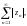 который является рядом с действительными
неотрицательными элементами.
который является рядом с действительными
неотрицательными элементами.
Справедливы утверждения
1. Пусть
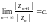 Если
Если
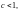 то ряд
сходится абсолютно, если
то ряд
сходится абсолютно, если
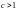 – ряд расходится.
– ряд расходится.
2. Пусть
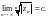 Если
то ряд
сходится абсолютно, если
– ряд расходится.
Если
то ряд
сходится абсолютно, если
– ряд расходится.
3. Если ряд сходится абсолютно, то он сходится.
З а м е ч а н и е. Из сходимости ряда не следует его абсолютная сходимость.
Абсолютная сходимость ряда с комплексными элементами равнозначна абсолютной сходимости его действительной и мнимой частей.
Ряд вида
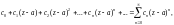 (29.24)
(29.24)
где
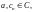
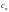 – коэффициенты ряда,
– коэффициенты ряда,
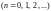
называется степенным рядом.
Теорема Абеля. Если степенной
ряд
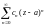 сходится в некоторой точке
сходится в некоторой точке
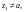 то он сходится, причем абсолютно, в любой
точке z, которая
удовлетворяет условию
то он сходится, причем абсолютно, в любой
точке z, которая
удовлетворяет условию
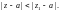
Если этот ряд расходится в некоторой
точке
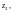 то он расходится во всех точках z,
для которых
то он расходится во всех точках z,
для которых
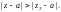
Пусть ряд
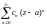 сходится более чем в одной точке, но не
на всей комплексной плоскости. Тогда
существует действительное число r
такое, что этот ряд абсолютно сходится
для всех z, для которых
сходится более чем в одной точке, но не
на всей комплексной плоскости. Тогда
существует действительное число r
такое, что этот ряд абсолютно сходится
для всех z, для которых
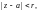 и расходится для тех z,
для которых
и расходится для тех z,
для которых
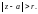 При этом круг
При этом круг
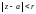 называется кругом сходимости,
число r – радиусом
сходимости степенного ряда.
называется кругом сходимости,
число r – радиусом
сходимости степенного ряда.
Пусть функция f(z)
является аналитической в круге
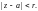 Тогда внутри этого круга функция f(z)
разлагается в степенной ряд по степеням
Тогда внутри этого круга функция f(z)
разлагается в степенной ряд по степеням
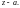 Такое разложение единственно.
Такое разложение единственно.
Признаки Д’Aламбера и Коши. Если существует
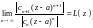 (29.25)
(29.25)
или соответственно
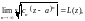 (29.26)
(29.26)
то ряд (29.24) сходится абсолютно во всех
точках z, для которых
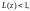 и расходится, если
и расходится, если
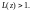
Степенной ряд вида
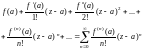 (29.27)
(29.27)
называется рядом Тейлора функции f(z), в окрестности точки a.
Функция f(z),
аналитическая в круге
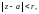 разлагается в этом круге в ряд Тейлора:
разлагается в этом круге в ряд Тейлора:
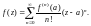 (29.28)
(29.28)
С учетом формулы (29.22), равенство (29.28) можно записать в виде
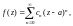
где
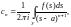
 – окружность
– окружность
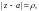
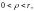
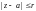 – круг аналитичности f(z).
– круг аналитичности f(z).
Ряд Тейлора (29.28), у которого
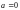 называется рядом Маклорена.
называется рядом Маклорена.
Общий вид ряда Маклорена:

Разложения в ряд Маклорена основных элементарных функций:
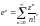
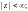
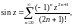
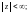 (29.29)
(29.29)
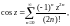 (29.30)
(29.30)
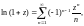
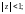
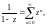
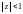 – геометрический ряд.
(29.31)
– геометрический ряд.
(29.31)
Ряд вида
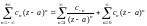 (29.32)
(29.32)
называется рядом Лорана, причем
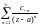 называется главной частью ряда
Лорана, а
– правильной частью ряда Лорана.
называется главной частью ряда
Лорана, а
– правильной частью ряда Лорана.
Функция f(z),
аналитическая в кольце
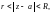 разлагается в этом кольце в абсолютно
сходящийся ряд Лорана
разлагается в этом кольце в абсолютно
сходящийся ряд Лорана
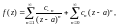 (29.33)
(29.33)
где коэффициенты определяются формулами:
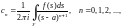
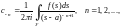
– окружность
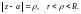
Разложение (29.33) в кольце
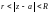 является единственным.
является единственным.
Заметим, что формулы для нахождения
коэффициентов
и
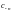 можно объединить в одну:
можно объединить в одну:
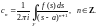
Пример 1. Исследовать сходимость ряда:
1)
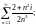 2)
2)
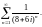
Решение.
1)
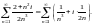 Рассмотрим ряды
Рассмотрим ряды
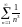 и
и
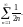 Ряд
сходится, так как это обобщенный
гармонический ряд
Ряд
сходится, так как это обобщенный
гармонический ряд
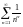 с
с
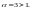 Ряд
Ряд
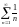 расходится (это гармонический ряд).
Значит,
расходится (это гармонический ряд).
Значит,
 где
где
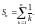 Так как
Так как
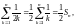 то
то
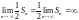
Отсюда следует,
что ряд
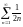 расходится, и, значит, исходный ряд
расходится, и, значит, исходный ряд
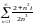 расходится.
расходится.
2) Ряд
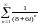 исследуем на абсолютную сходимость,
для чего рассмотрим
исследуем на абсолютную сходимость,
для чего рассмотрим
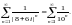
Последний ряд
сходится (сходящаяся геометрическая
прогрессия с
 ).
Значит, ряд
).
Значит, ряд
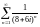 сходится абсолютно.
сходится абсолютно.
Пример 2. Исследовать на сходимость ряд:
1)
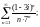 2)
2)
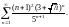
Решение. 1) Рассмотрим ряд из модулей его элементов:
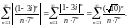
Для выяснения вопроса сходимости полученного знакоположительного ряда используем признак Коши:
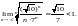
Это значит, что данный ряд сходится абсолютно, а поэтому сходится.
2) Исследование на сходимость ряда из модулей
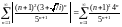
проведем на основе признака Д’Aламбера:
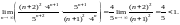
Последнее означает абсолютную сходимость данного ряда, чем гарантируется его сходимость.
Пример 3. Исследовать на сходимость ряд
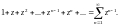
Решение.
Функции-слагаемые
 данного ряда определены на всей плоскости
C.
Его n-я
частичная сумма есть
данного ряда определены на всей плоскости
C.
Его n-я
частичная сумма есть
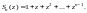
Методом математической индукции нетрудно убедиться в том, что
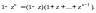
Тогда
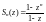
или, то же самое,
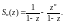
Если – произвольное комплексное число, то данный функциональный ряд преобразуется в числовой с частичной суммой
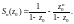
Поэтому,
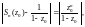
откуда
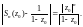
Из последнего
отношения видно, что только для того
числа
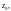 для которого
для которого
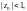 выполняется условие
выполняется условие
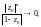 когда
когда
Это означает, что
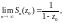 если
если
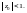
Произвольность
числа
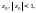 приводит к заключению, что внутри круга
приводит к заключению, что внутри круга
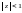 ряд сходится к сумме
ряд сходится к сумме
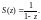
Если
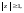 то общий элемент
то общий элемент
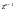 данного ряда не стремится к нулю с ростом
n
(необходимый признак сходимости не
выполняется), а потому ряд расходится.
данного ряда не стремится к нулю с ростом
n
(необходимый признак сходимости не
выполняется), а потому ряд расходится.
Таким образом, получена формула
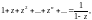 где
где
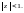
В
заключение заметим, что полученный
результат полностью соответствует
действительному случаю, где для суммы
бесконечно убывающей геометрической
прогрессии имеем
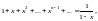 если
если
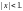
Пример 4. Найти множество абсолютной сходимости ряда
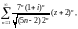 пользуясь признаком
Д’Aламбера.
пользуясь признаком
Д’Aламбера.
Решение. Используя формулу (29.25), получим:
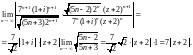
Если
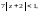 то ряд является абсолютно сходящимся.
Очевидно, что это имеет место внутри
круга
то ряд является абсолютно сходящимся.
Очевидно, что это имеет место внутри
круга
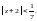 Одновременно с этим признак Д’Aламбера
утверждает, что вне круга (т. е. при
Одновременно с этим признак Д’Aламбера
утверждает, что вне круга (т. е. при
 )
ряд расходится, однако он не достаточно
«сильный», чтобы дать ответ о сходимости
в точках окружности
)
ряд расходится, однако он не достаточно
«сильный», чтобы дать ответ о сходимости
в точках окружности
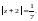
Пример 5.
Найти круг и радиус сходимости степенного
ряда
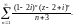
Решение.
Используем признак Д'Аламбера и рассмотрим
предел
 т. е.
т. е.
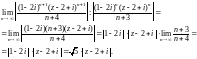
По признаку Д'Аламбера ряд сходится, если
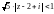 или
или
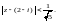
Значит, круг
сходимости есть
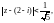 радиус сходимости
радиус сходимости
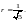
Пример 6. Разложить
в ряд Тейлора по степеням
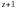 функцию:
функцию:
1)
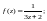 2)
2)
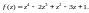
Найти область сходимости полученного ряда.
Решение. 1) Решим задачу двумя способами.
1-й способ.
Используем формулу (29.28) для
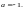 Для этого найдем производные функции
и их значения в точке
Для этого найдем производные функции
и их значения в точке
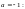
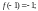
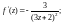
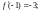
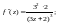
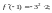
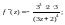
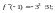
………………………… ……………………
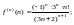
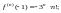
………………………… ……………………
Тогда получаем
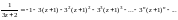
Радиус сходимости полученного ряда найдем согласно формуле
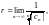
т. е.
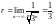
Значит, ряд сходится
внутри круга
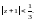
2-й способ. Запишем выражение, которое задает функцию f(z), в другом виде:
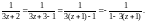
Полученную дробь
рассмотрим как сумму геометрической
прогрессии со знаменателем
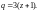
Если
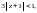 то
то
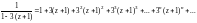
Поэтому заданная функция раскладывается в ряд того же вида, который мы получили первым способом.
2) Для того чтобы получить разложение функции
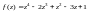 в
ряд Тейлора на основе формулы (29.28),
вычислим значения ее производных в
точке
Сразу заметим, что данная функция есть
многочлен 4-й степени, а поэтому все
производные, начиная с пятой, будут
равны нулю. Получаем
в
ряд Тейлора на основе формулы (29.28),
вычислим значения ее производных в
точке
Сразу заметим, что данная функция есть
многочлен 4-й степени, а поэтому все
производные, начиная с пятой, будут
равны нулю. Получаем
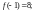
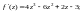
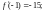

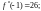
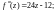
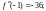
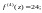
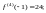
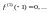
Тогда
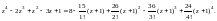
Логично, что для многочлена 4-й степени ряд Тейлора приобретает вид тоже многочлена 4-й степени. И это равенство справедливо на всей комплексной плоскости.
Пример 7. Найти
круг сходимости ряда
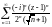 и исследовать его сходимость в точках
и исследовать его сходимость в точках
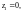
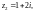
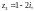
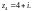
Решение.
Рассмотрим ряд из модулей членов, т. е.
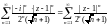 и вычислим предел
и вычислим предел
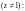

Значит, по признаку
Д’Aламбера,
круг сходимости определяется неравенством
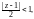 т. е.
т. е.
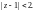
Для
имеем
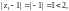 т. е.
точка
лежит внутри круга сходимости, значит,
исходный ряд в этой точке сходится
абсолютно.
т. е.
точка
лежит внутри круга сходимости, значит,
исходный ряд в этой точке сходится
абсолютно.
Для
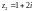 получаем
получаем
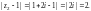
Точка
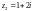 лежит на границе круга сходимости. Из
общей теории необходимо сделать вывод
о сходимости ряда в этой точке. Исследуем
числовой ряд, который получается из
исходного степенного ряда при значении
лежит на границе круга сходимости. Из
общей теории необходимо сделать вывод
о сходимости ряда в этой точке. Исследуем
числовой ряд, который получается из
исходного степенного ряда при значении
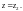 Имеем ряд
Имеем ряд
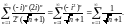
Ряд
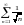 расходится (как ряд Дирихле с
расходится (как ряд Дирихле с
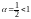 ).
Применяя предельный признак сравнения,
делаем вывод, что ряд
).
Применяя предельный признак сравнения,
делаем вывод, что ряд
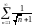 расходится. Исходный ряд в точке
расходится.
расходится. Исходный ряд в точке
расходится.
Для
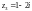 имеем
имеем
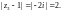
Точка
лежит на окружности, ограничивающей
круг сходимости. При
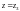 исходный ряд имеет вид
исходный ряд имеет вид
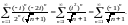
Этот ряд не сходится абсолютно (как было показано выше), но он является знакочередующимся и для него выполняются оба условия теоремы Лейбница. По признаку Лейбница этот ряд сходится условно. Исходный ряд в точке сходится.
Для
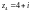 выполняется
выполняется
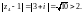 Значит, точка
лежит вне круга сходимости, и поэтому
исходный ряд в этой точке расходится.
Значит, точка
лежит вне круга сходимости, и поэтому
исходный ряд в этой точке расходится.
Пример 8. Разложить в ряд Маклорена функцию:
1)
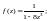 2)
2)
Решение.
1) Используем формулу (29.31), заменяя в ней
переменную z
на
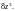 Тогда ряд Маклорена примет вид
Тогда ряд Маклорена примет вид
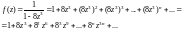
Он сходится при
условии
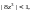 т. е.
внутри круга
т. е.
внутри круга
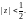
2) Сначала понизим степень косинуса:

Далее, используя разложение (29.30), получим:
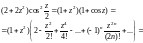


Приводя подобные, приходим к ответу
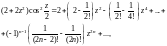
что ряд сходится на всей плоскости C.
Пример 9. Разложить
в ряд Тейлора в окрестности точки
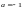 функцию
функцию
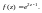
Решение. Этот пример можно решить согласно общему подходу, основываясь на формуле (29.28). Мы же используем ряд Маклорена (29.29). Для этого сделаем следующие преобразования:
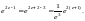
Тогда
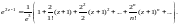
Ряд сходится на всей комплексной плоскости.
Пример 10. Найти область сходимости ряда
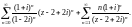
Решение.
Данный ряд есть сумма рядов по положительным
и отрицательным степеням разности
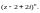 Для первого ряда (как для степенного)
используем признак Коши:
Для первого ряда (как для степенного)
используем признак Коши:
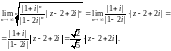
Ряд сходится, если
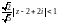 или, то же самое,
или, то же самое,
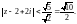
Значит, первый ряд сходится внутри круга:
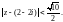
Для второго ряда применим признак Д’Aламбера:
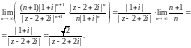
Ряд сходится, если
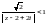 или
или
 т. е.
т. е.
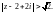
Полученные множества сходимости пересекаются, в результате чего мы имеем область сходимости данного ряда – кольцо
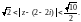
Пример 11. Разложить в ряд Лорана функцию
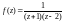 по степеням z.
по степеням z.
Решение.
Нетрудно увидеть, что
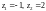 – особые точки данной функции. Это
означает, что существуют три области,
внутри которых функция аналитична:
(область
– особые точки данной функции. Это
означает, что существуют три области,
внутри которых функция аналитична:
(область
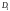 );
);
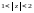 (область
(область
 );
);
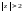 (область
(область
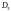 )
(рис. 29.3).
)
(рис. 29.3).
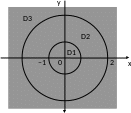
Рис. 29.3
В каждой из трех областей функция f(z) будет представляться своим рядом Лорана. Запишем функцию сначала в виде
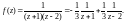
Рассмотрим область
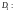
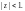 Представим функцию
Представим функцию
 как сумму
соответствующих геометрических
прогрессий (имеем право сделать это,
так как в области
выполняется
и
как сумму
соответствующих геометрических
прогрессий (имеем право сделать это,
так как в области
выполняется
и
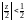 ).
Тогда по формуле суммы (см. формулу
(29.31)) получаем следующее представление
функции рядом Лорана
).
Тогда по формуле суммы (см. формулу
(29.31)) получаем следующее представление
функции рядом Лорана
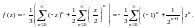
Видим,
что ряд Лорана в области
содержит только правильную часть, т. е.
имеет вид степенного. Это не случайно,
так как мы рассматриваем разложение в
круге
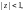 в котором функция аналитична.
в котором функция аналитична.
Рассмотрим область
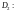
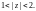 Тогда имеет смысл записать функцию в
виде
Тогда имеет смысл записать функцию в
виде
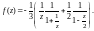
Так как в области
выполняется
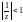 и
и
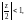 поэтому, по формуле суммы геометрического
ряда, имеем разложение
поэтому, по формуле суммы геометрического
ряда, имеем разложение
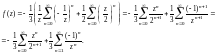
Полученный ряд Лорана содержит и правильную, и главную части.
Рассмотрим область
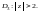 Функцию f(z)
запишем в виде
Функцию f(z)
запишем в виде
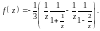 Поскольку в области
выполняется
Поскольку в области
выполняется
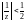 и
и
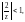 то на основе формулы суммы геометрического
ряда получаем следующее разложение:
то на основе формулы суммы геометрического
ряда получаем следующее разложение:
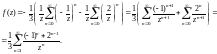
Замечаем, что полученный ряд Лорана содержит только главную часть.
Пример 12. Разложить
функцию
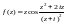 в ряд Лорана по степеням
в ряд Лорана по степеням

Решение.
Точка
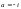 – единственная (на плоскости C)
особая точка данной функции. Это означает,
что можно построить кольцо
– единственная (на плоскости C)
особая точка данной функции. Это означает,
что можно построить кольцо
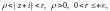 в котором функция является аналитической.
Преобразуем выражение:
в котором функция является аналитической.
Преобразуем выражение:
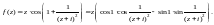
Далее используем
разложения в ряд Маклорена (29.29) и (29.30),
в которых вместо z
возьмем
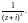 Тогда
Тогда
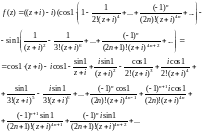
Видим, что полученный ряд Лорана данной функции содержит только два слагаемых правильной части и бесконечное множество слагаемых главной части.
Задания
I уровень
1.1.
Разложите функцию f(z)
в ряд Тейлора по степеням
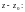
1)
 2)
2)
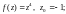
3)
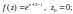 4)
4)
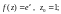
5)
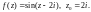
1.2. Найдите круг сходимости степенного ряда:
1)
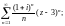 2)
2)
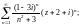
3)
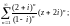 4)
4)
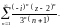
1.3. Найдите кольцо сходимости ряда Лорана:
1)
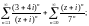 2)
2)
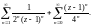
II уровень
2.1. Разложите функцию f(z) в ряд Лорана в окрестности точки
1)
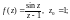 2)
2)
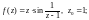
3)
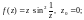 4)
4)
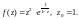
2.2. Разложите функцию f(z)
в ряд Лорана по степеням
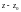 в кольце D:
в кольце D:
1)
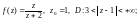
2)
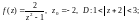
3)
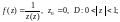
4)

2.3. Определите круг сходимости
заданного ряда и исследуйте его сходимость
в точках
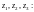
1)
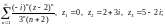
2)
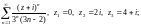
3)
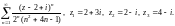
III уровень
3.1. Разложите функцию f(z) в ряд Лорана по степеням во всех областях аналитичности:
1)
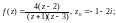
2)
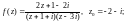
3)
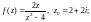
4)
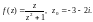
3.2. Разложите в ряд Лорана функцию
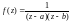 при
при
 и при
и при
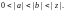
29.8. Нули и особые точки функции
Нулем аналитической в области
D функции
f(z)
называется комплексное число
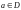 такое, что
такое, что
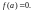
Если
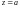 есть нуль функции f(z),
то
есть нуль функции f(z),
то
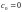 в разложении функции f(z)
в ряд Тейлора.
в разложении функции f(z)
в ряд Тейлора.
Точка a называется нулем кратности k (порядка k) функции f(z), если в разложении
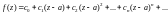 (29.34)
(29.34)
выполняется
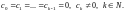 При
При
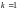 нуль функции называют простым нулем.
нуль функции называют простым нулем.
В случае нуля кратности k разложение имеет вид:
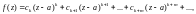
т. е.
 (29.35)
(29.35)
где
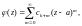
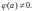
Заметим, что точка является нулем кратности k, если
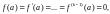
 (29.36)
(29.36)
Точка называется изолированным нулем функции f(z), если в области D существует окрестность с центром в точке a, которая не содержит других нулей этой функции.
Справедливо утверждение: нули аналитической
в области D функции
f(z)
изолированы, если
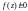 на множестве D.
на множестве D.
Точка
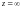 называется нулем кратности k
функции f(z),
если ее ряд Лорана, построенный в
окрестности точки
не имеет главной части, а для коэффициентов
правильной части выполняются условия
называется нулем кратности k
функции f(z),
если ее ряд Лорана, построенный в
окрестности точки
не имеет главной части, а для коэффициентов
правильной части выполняются условия
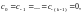
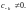 (29.37)
(29.37)
При выполнении условий (29.37) ряд Лорана функции f(z) в окрестности точки имеет вид:
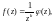 (29.38)
(29.38)
где
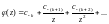
Точка в которой функция f(z) является аналитической, называется правильной точкой функции. Если функция f(z) аналитична в некоторой проколотой окрестности точки и не аналитична в самой точке (или не определена в ней), то называется изолированной особой точкой функции f(z).
Будем говорить, что функция f(z)
является аналитической в бесконечно
удаленной точке
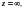 если функция
если функция
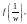 где
где

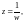 является аналитической в точке
является аналитической в точке
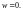 Точка
называется особой точкой
функции f(z),
если точка
Точка
называется особой точкой
функции f(z),
если точка
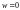 является особой для функции
является особой для функции
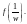 Особая точка
является изолированной, если
существует окрестность
Особая точка
является изолированной, если
существует окрестность
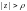 такая, которая не содержит других особых
точек функции f(z)
(кроме
).
такая, которая не содержит других особых
точек функции f(z)
(кроме
).
Если выполняются условия:
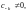
ряд Лорана функции f(z)
в окрестности точки
имеет вид

где
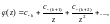 причем
причем

Особая точка a (изолированная особая точка) функции f(z) называется устранимой, если ряд Лорана (29.32) этой функции в проколотой окрестности точки a не содержит главной части.
Особая точка a функции f(z) является устранимой тогда и только тогда, когда f(z) ограничена в проколотой окрестности точки a.
Можно дать и такое определение устранимой
особой точки: точка a
называется устранимой особой точкой
функции f(z),
если существует конечный предел
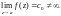
Особая точка a функции f(z) называется полюсом, если ряд Лорана этой функции в проколотой окрестности точки a содержит конечное число элементов главной части, т. е. имеет вид
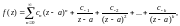
где
При этом точка a
называется полюсом
k-го
порядка
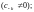 при
полюс еще
называют простым
полюсом.
при
полюс еще
называют простым
полюсом.
Особая точка a функции
f(z)
является полюсом тогда и только тогда,
когда
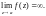
Справедливо утверждение: если точка a
является полюсом k-го
порядка функции f(z)
(или нулем кратности k),
то для функции
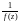 точка a является нулем
кратности k (соответственно
полюсом порядка k).
точка a является нулем
кратности k (соответственно
полюсом порядка k).
Если функция f(z) имеет вид
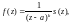 (29.39)
(29.39)
где s(z)
– аналитическая функция и
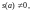 то точка
есть полюс порядка k
функции f(z).
то точка
есть полюс порядка k
функции f(z).
Точка a называется
существенно особой точкой
функции f(z),
если ряд Лорана этой функции в проколотой
окрестности точки a
содержит бесконечное количество
ненулевых элементов главной части.
Можно дать и такое определение: точка
a называется существенно
особой точкой функции f(z),
если
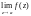 не существует.
не существует.
Пусть функция f(z)
разложена в ряд Лорана в окрестности
точки
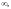 т. е.
т. е.
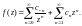 (29.40)
(29.40)
Бесконечно удаленная точка
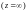 называется:
называется:
1) устранимой особой точкой функции f(z), если ее разложение (29.40) в ряд Лорана не содержит положительных степеней z;
2) полюсом порядка k,
если разложение содержит конечное число
элементов с положительными степенями
z, причем последним
ненулевым коэффициентом является
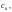
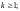
3) существенно особой точкой, если это разложение содержит бесконечное число положительных степеней z.
Пример 1. Найти
нули функции
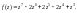
Решение. Данная функция является многочленом седьмой степени. Нули этой функции являются корнями многочлена. Поскольку
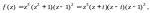
то
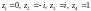 – нули данной функции.
– нули данной функции.
Других нулей нет, так как нет других корней многочлена.
Пример 2.
Определить порядок нуля
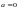 функции:
функции:
1)
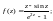 2)
2)
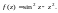
Решение.
1) Используем разложения функций
 и
и
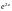 в ряд Маклорена. Согласно формулам
(29.29), получаем
в ряд Маклорена. Согласно формулам
(29.29), получаем
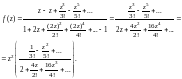
Поскольку при
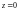 функция, которая стоит в скобках, не
равна нулю, то, согласно равенству
(29.35), значение
есть нуль кратности два.
функция, которая стоит в скобках, не
равна нулю, то, согласно равенству
(29.35), значение
есть нуль кратности два.
2) Используем другой
способ исследования кратности нуля –
проверим выполнение условий (29.36) в точке
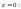
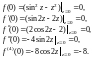
Учитывая то, что
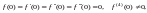
приходим к заключению, что есть нуль кратности четыре.
Пример 3.
Выяснить, является ли точка
 нулем функции
нулем функции
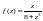 и какой кратности (если это нуль).
и какой кратности (если это нуль).
Решение. Преобразуем выражение, которым определяется функция, к виду
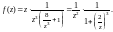
Для окрестности
 бесконечно удаленной точки имеем
бесконечно удаленной точки имеем
 Поэтому, используя формулу суммы
геометрического ряда, получаем
Поэтому, используя формулу суммы
геометрического ряда, получаем
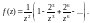
Сопоставляя полученное равенство с формулой (29.38), приходим к заключению, что есть нуль данной функции кратности два.
Пример 4. Найти особые точки функции и определить их тип:
1)
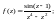 2)
2)
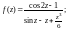 3)
3)
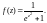
Решение.
1) Очевидно, что для
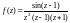 особыми точками функции являются нули
знаменателя. Поскольку числитель не
равен нулю при
и
особыми точками функции являются нули
знаменателя. Поскольку числитель не
равен нулю при
и
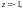 то значения 0, – 1
есть соответственно полюс кратности
два и простой полюс. Точку
то значения 0, – 1
есть соответственно полюс кратности
два и простой полюс. Точку
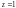 надо исследовать отдельно. Для этого
вычислим следующий предел:
надо исследовать отдельно. Для этого
вычислим следующий предел:
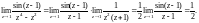
(убедиться
в том, что последний предел равнен 1,
можно, например, разложив
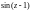 в ряд Тейлора по степеням (z – 1)).
Получив предел
в ряд Тейлора по степеням (z – 1)).
Получив предел
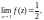 приходим к заключению, что
– устранимая особая точка.
приходим к заключению, что
– устранимая особая точка.
2) Видно, что особой
точкой функции является точка
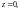 в которой знаменатель принимает нулевое
значение. Однако числитель дроби тоже
равен нулю для
а поэтому сразу определить тип особой
точки мы не можем. Для его определения
разложим функции
в которой знаменатель принимает нулевое
значение. Однако числитель дроби тоже
равен нулю для
а поэтому сразу определить тип особой
точки мы не можем. Для его определения
разложим функции
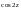 и
в ряд Маклорена. Получим
и
в ряд Маклорена. Получим
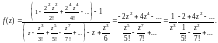
Поскольку степенные ряды, которые стоят в числителе и знаменателе последней дроби, представляют аналитические и отличные от нуля функции в окрестности точки то данная функция может быть записана в виде
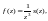
где
s(z)
– аналитическая функция,
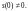 В соответствии с формулой (29.39) приходим
к заключению, что точка
есть полюс 3-го порядка.
В соответствии с формулой (29.39) приходим
к заключению, что точка
есть полюс 3-го порядка.
3) Рассмотрим
функцию
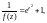 которая является знаменателем данной
дроби. Найдем ее нули:
которая является знаменателем данной
дроби. Найдем ее нули:
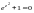 – то самое, что
– то самое, что
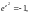 т. е.
т. е.
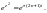 Поэтому нули этой функции есть
Поэтому нули этой функции есть
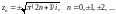 Определим кратность полученных нулей.
Поскольку
Определим кратность полученных нулей.
Поскольку
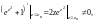
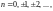 то
все точки zn
– простые нули.
Тогда для данной функции эти точки есть
простые полюсы, причем их бесконечно
много (на координатной плоскости они
размещаются на двух биссектрисах
координатных углов).
то
все точки zn
– простые нули.
Тогда для данной функции эти точки есть
простые полюсы, причем их бесконечно
много (на координатной плоскости они
размещаются на двух биссектрисах
координатных углов).
Пример 5.
Найти особые точки функции
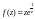 и выяснить их тип.
и выяснить их тип.
Решение. Очевидно, что функция определена и дифференцируема на всей комплексной плоскости, кроме точки Выясним тип особой точки, разложив данную функцию в ряд Лорана в окрестности этой точки. Для этого воспользуемся формулой (29.29) для представления экспоненты рядом Маклорена. Получим
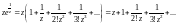
Ряд содержит бесконечное количество слагаемых в главной части, т. е. – существенно особая точка функции.
Задания
I уровень
1.1. Найдите нули функции f(z) и определите их кратности:
1)
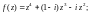 2)
2)
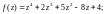
3)
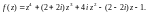
1.2. Найдите особые точки функции f(z) и определите характер каждой особой точки (в случае полюса определите его порядок):
1)
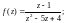 2)
2)
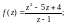 3)
3)
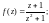
4)
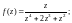 5)
5)

II уровень
2.1. Найдите нули функции f(z) и определите их кратности:
1)
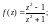 2)
2)
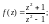 3)
3)
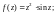
4)
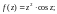 5)
5)
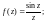 6)
6)
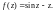
2.2. Найдите особые точки функции f(z) и определите характер каждой особой точки (в случае полюса определите его порядок):
1)
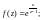 2)
2)
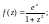 3)
3)
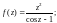
4)
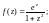 5)
5)
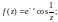 6)
6)
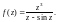
III уровень
3.1. При условии, что функции f(z)
и g(z)
имеют в точке
полюсы порядка m и
порядка n соответственно,
определите, является ли точка
особой для функции
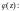
1)
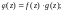 2)
2)
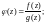 3)
3)
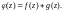
Если точка a является особой точкой, установите ее тип.
3.2. Определите, является ли точка особой для функции f(z):
1)
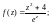 2)
2)
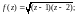
3)
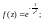 4)
4)
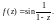
Если да, то каков ее характер?
29.9. Вычеты и их приложения
Вычетом функции f(z) в особой точке a называется коэффициент при первой отрицательной степени ряда Лорана функции f(z) в проколотой окрестности точки a:
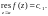 (29.41)
(29.41)
Вычет функции f(z) в особой точке a может быть найден по формуле:
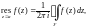 (29.42)
(29.42)
где
– положительно ориентированная
окружность
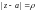 такая, что функция f(z)
аналитична всюду на круге
такая, что функция f(z)
аналитична всюду на круге
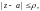 за исключением точки
за исключением точки
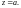
Если a
– устранимая особая точка функции f(z),
то
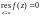 и, значит,
и, значит,
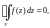 где контур
положительно
ориентированная окружность
где контур
положительно
ориентированная окружность
 такая, что f(z)
аналитична всюду на круге
такая, что f(z)
аналитична всюду на круге
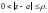
Если a – простой полюс функции f(z), то
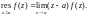 (29.43)
(29.43)
Если функцию f(z) можно записать в виде:
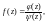
где
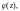
 аналитичны в точке a
и
аналитичны в точке a
и

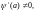
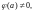 т. е. a
– простой полюс функции f(z),
то
т. е. a
– простой полюс функции f(z),
то
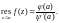 (29.44)
(29.44)
Если a – полюс k-го порядка функции f(z), то
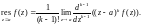 (29.45)
(29.45)
Основная теорема о вычетах.
Пусть функция f(z)
является аналитической во всех точках
односвязной области D,
кроме конечного числа особых точек, и
Г – замкнутая положительно ориентированная
кривая, которая лежит в D
и ограничивает область, содержащую
особые точки
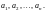 Тогда
Тогда
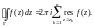 (29.46)
(29.46)
Вычетом функции f(z) в точке ( – изолированная особая точка функции f(z)) называется число, равное противоположному по знаку коэффициенту при первой отрицательной степени ряда Лорана функции f(z) в окрестности точки
 (29.47)
(29.47)
Вычет функции f(z) в точке может быть найден по формуле:
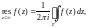 (29.48)
(29.48)
где
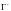 – окружность достаточно большого
радиуса, проходимая по часовой стрелке.
– окружность достаточно большого
радиуса, проходимая по часовой стрелке.
В устранимой особой точке вычет может быть и ненулевым (в отличие от конечной устранимой особой точки).
Теорема. Пусть функция f(z) аналитична на плоскости Ĉ, кроме конечного числа точек. Тогда сумма вычетов во всех особых точках, включая и точку равна нулю.
Пусть функция f(z)
аналитична всюду на полуплоскости
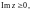 кроме конечного числа особых точек,
которые лежат сверху от действительной
оси. Пусть также точка
является нулем кратности больше единицы
функции f(z).
Тогда справедлива формула
кроме конечного числа особых точек,
которые лежат сверху от действительной
оси. Пусть также точка
является нулем кратности больше единицы
функции f(z).
Тогда справедлива формула
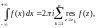 (29.49)
(29.49)
где
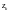 – особые точки функции f(z),
в которых
– особые точки функции f(z),
в которых
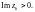
Пусть дробно-рациональная функция
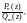 где
где
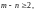 является аналитической на действительной
оси. Тогда
является аналитической на действительной
оси. Тогда
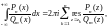 (29.50)
(29.50)
где
– полюсы функции
которые лежат в полуплоскости

Если
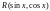 – дробно-рациональная функция от
– дробно-рациональная функция от
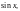
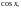 то
то
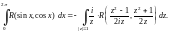
Пример 1. Вычислить вычет функции:
1)
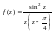 в точке
в точке
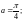 2)
2)
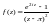 в точке
в точке
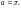
Решение.
1) Очевидно, что
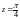 есть простой полюс функции. Найти вычет
в этой точке можно двумя способами:
согласно формулам (29.43) и (29.44). Покажем
это.
есть простой полюс функции. Найти вычет
в этой точке можно двумя способами:
согласно формулам (29.43) и (29.44). Покажем
это.
Используя формулу (29.43), получаем:
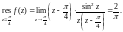
Заданная функция удовлетворяет всем условиям, при которых справедлива формула (29.44). Поэтому,
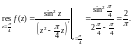
2) Поскольку, в соответствии с формулой Эйлера,
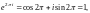
то
числитель и знаменатель заданной функции
зануляются в точке
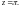 Для выяснения характера особой точки
Для выяснения характера особой точки
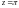 разложим числитель в ряд Тейлора по
степеням
разложим числитель в ряд Тейлора по
степеням
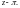 Найдем коэффициенты этого ряда:
Найдем коэффициенты этого ряда:
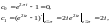
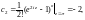
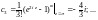
Получаем
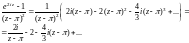
Видим, что – простой полюс данной функции. Однако использовать формулу (29.43) или (29.44) уже не надо. Из полученного разложения имеем:
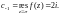
Пример 2. Вычислить вычет в точке функции:
1)
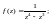 2)
2)
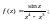 3)
3)
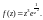
Решение. 1) Поскольку
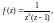
то
есть полюс третьего порядка заданной
функции. Тогда согласно формуле (29.45),
при
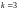 имеем:
имеем:
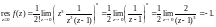
2) Запишем данную функцию в виде
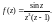 (29.51)
(29.51)
Выражение (29.51)
показывает, что точка
есть нуль кратности три знаменателя.
Однако в этой точке и числитель равен
нулю, причем для него
есть простой нуль (это следует из
разложения функции
в ряд Маклорена – формула (29.29)). Значит,
в отличие от первой функции, рассмотренной
в этом примере, точка
есть полюс второго порядка. Для вычисления
вычета в ней воспользуемся формулой
(29.45) для
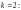
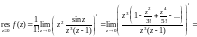
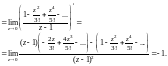
3) Чтобы определить
характер особой точки
для данной функции, лучше всего
использовать разложение экспоненты в
ряд Маклорена (29.29), заменив в нем z
на
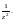 Тогда
Тогда
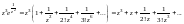
Видим, что коэффициент
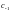 равен
равен
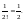 Значит,
Значит,
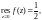 причем точка
существенно особая точка.
причем точка
существенно особая точка.
Пример 3. Вычислить интеграл от функции
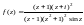
по положительно ориентированной окружности:
1)
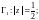 2)
2)
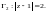
Решение.
Найдем особые точки подынтегральной
функции и определим их тип. Нули
знаменателя – точки
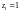 (простой нуль);
(простой нуль);
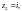
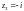 (двукратные нули);
(двукратные нули);
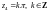 (простые нули). С учетом того, что
(простые нули). С учетом того, что
 – нуль кратности два числителя, приходим
к заключению, что
– нуль кратности два числителя, приходим
к заключению, что
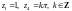 – простые полюсы;
– простые полюсы;
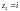 – полюс второго порядка,
– устранимая особая точка. Вычислим
интеграл от данной функции, основываясь
на формуле (29.46).
– полюс второго порядка,
– устранимая особая точка. Вычислим
интеграл от данной функции, основываясь
на формуле (29.46).
1) Внутри линии
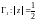 находится только одна особая точка
находится только одна особая точка
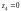 (при
(при
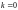 ).
).
Используя формулы (29.46) и (29.43), получаем:
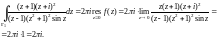
2) Линия
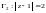 имеет внутри четыре особые точки:
имеет внутри четыре особые точки:
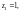
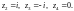 Поэтому надо вычислить четыре вычета.
Поэтому надо вычислить четыре вычета.
Поскольку – простой полюс, то по формуле (29.43) получаем:
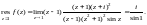
Для вычисления вычета в полюсе второго порядка воспользуемся формулой (29.45):
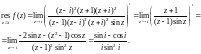
Поскольку
– устранимая особая точка, то
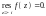
Вычет в точке находим, используя формулу (29.43). Получаем
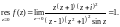
Воспользуемся теперь формулой (29.46) и полученными значениями вычетов:
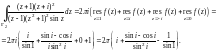
Пример 4.
Вычислить
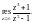
Решение. Преобразуем выражение, которое стоит под знаком вычета:
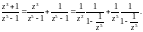
Теперь используем разложение (29.31):
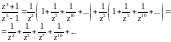
Видим, что
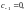 т. е.
т. е.
Пример 5.
Вычислить
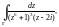
где Г – окружность
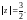
Решение.
Внутри окружности
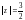 лежат шесть полюсов третьего порядка,
вне ее – простой полюс
лежат шесть полюсов третьего порядка,
вне ее – простой полюс
 и точка
и точка
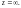 Очевидно, что более рационально вычислять
сумму вычетов в точках
и
Согласно формуле (29.43), получаем:
Очевидно, что более рационально вычислять
сумму вычетов в точках
и
Согласно формуле (29.43), получаем:
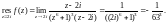
Для
определения вычета в точке
найдем несколько слагаемых ряда Лорана.
С этой целью сделаем замену переменной
 Тогда
Тогда
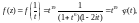
где через
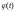 обозначена аналитическая функция в
окрестности точки
обозначена аналитическая функция в
окрестности точки
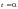 Функцию
можно разложить в степенной ряд:
Функцию
можно разложить в степенной ряд:
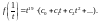
Возвращаясь к старой переменной, имеем:
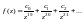
Видим, что
т. е.
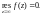 Получили следующее значение интеграла:
Получили следующее значение интеграла:
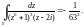
Пример 6. Вычислить
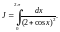
Решение.
Сделаем замену переменной
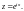 Тогда
Тогда
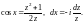
Приходим к необходимости вычисления интеграла
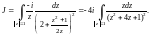
Найдем
особые точки подынтегральной функции.
Это те значения z,
для которых
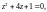 т. е.
т. е.
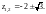
Внутри круга
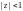 лежит только точка
лежит только точка
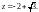 Для подынтегральной функции она является
полюсом второго порядка. Значит,
Для подынтегральной функции она является
полюсом второго порядка. Значит,
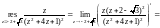

По формуле (29.46) получаем
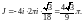
Пример 7.
Вычислить интеграл

Решение.
Функция
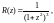 которая является подынтегральной при
которая является подынтегральной при
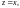 удовлетворяет всем условиям, при которых
справедлива формула (29.50). Ее особыми
точками являются точки
удовлетворяет всем условиям, при которых
справедлива формула (29.50). Ее особыми
точками являются точки
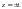 Это полюсы третьего порядка. В верхней
полуплоскости лежит только полюс
Это полюсы третьего порядка. В верхней
полуплоскости лежит только полюс
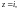 а поэтому
а поэтому
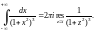
Находим
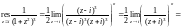
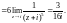
Получаем
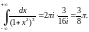
Задания
