
- •29. Теория функций комплексной
- •29.1. Основные понятия теории функций
- •I уровень
- •II уровень
- •III уровень
- •29.2. Функция комплексной переменной,
- •I уровень
- •II уровень
- •III уровень
- •29.4. Однозначные элементарные функции
- •1. Экспонента
- •2. Тригонометрические функции
- •3. Гиперболические функции
- •I уровень
- •II уровень
- •III уровень
- •29.7. Ряды на комплексной плоскости
- •I уровень
- •II уровень
- •III уровень
29. Теория функций комплексной
ПЕРЕМЕННОЙ
29.1. Основные понятия теории функций
комплексной переменной
Множество всех комплексных чисел обозначают С. Между множеством С и множеством точек (x, y) плоскости xOy существует взаимно однозначное соответствие. Плоскость xOy называют комплексной плоскостью (плоскостью C).
Множество C пополняют
элементом
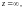 который называется бесконечностью
или бесконечно удаленной точкой.
Комплексная
плоскость, которую пополнили бесконечностью,
называется расширенной
комплексной плоскостью и обозначается
Ĉ.
который называется бесконечностью
или бесконечно удаленной точкой.
Комплексная
плоскость, которую пополнили бесконечностью,
называется расширенной
комплексной плоскостью и обозначается
Ĉ.
Множество точек
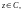 которые лежат внутри круга радиуса
которые лежат внутри круга радиуса
 с центром в точке
с центром в точке
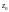 называется -окрестностью
точки z0,
т. е.
называется -окрестностью
точки z0,
т. е.
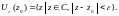
Проколотой -окрестностью точки z0 называется ее -окрестность без центра z0.
Для бесконечной
точки
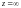 из расширенной плоскости Ĉ
понятие -окрестности
определяется как множество точек,
которые находятся вне круга радиуса
с центром в начале системы координат,
т. е.
это множество точек z,
для которых
из расширенной плоскости Ĉ
понятие -окрестности
определяется как множество точек,
которые находятся вне круга радиуса
с центром в начале системы координат,
т. е.
это множество точек z,
для которых
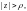
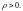
Множество D называют ограниченным, если существует круг конечного радиуса с центром в начале системы координат, который содержит это множество.
Точка
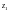 называется внутренней для
множества D, если
существует окрестность этой точки,
целиком содержащаяся внутри множества
D. Множество D,
которое содержит только внутренние
точки, называется открытым множеством.
называется внутренней для
множества D, если
существует окрестность этой точки,
целиком содержащаяся внутри множества
D. Множество D,
которое содержит только внутренние
точки, называется открытым множеством.
Связным называется множество, любые две точки которого можно соединить непрерывной линией, целиком принадлежащей множеству. Множество D точек комплексной плоскости называют областью, если оно является открытым и связным.
Граничной точкой области D
называется такая точка, которая сама
не принадлежит D, но
в любой ее окрестности есть точки области
D. Совокупность всех
граничных точек области D
называется ее границей. Область
D с присоединенной к
ней границей Г называется замкнутой
областью
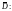
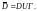
Точки комплексной плоскости, которые
не принадлежат
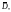 называются внешними для области
D.
называются внешними для области
D.
Предел последовательности комплексных чисел
Последовательность
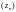 комплексных чисел определяется как
функция натурального аргумента, которая
каждому значению
комплексных чисел определяется как
функция натурального аргумента, которая
каждому значению
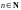 ставит в соответствие единственное
комплексное число
ставит в соответствие единственное
комплексное число
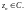
Число
 называется пределом
последовательности
называется пределом
последовательности
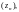
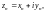 если для любого
если для любого
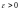 существует число
существует число
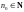 такое, что для любого номера
такое, что для любого номера
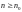 выполняется:
выполняется:
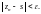
Факт, что последовательность имеет предел s, записывают так:
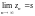 (или
(или
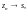
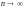 ).
).
Последовательность имеющая предел, называется сходящейся.
Используя понятие -окрестности,
предел последовательности определяют
и так: число
называется пределом последовательности
если для любого
существует такой номер
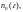 что, начиная с него, все элементы
последовательности находятся в
-окрестности
точки .
что, начиная с него, все элементы
последовательности находятся в
-окрестности
точки .
Свойства предела последовательности комплексных чисел
1. Для того, чтобы выполнялось равенство
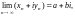 (29.1)
(29.1)
необходимо и достаточно, чтобы выполнялись равенства:
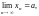
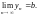 (29.2)
(29.2)
2. Из того, что
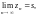 следует
следует
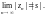
3. Если
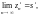 то
то
а)
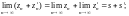
б)
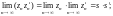
в)
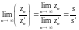
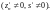
Последовательность
 называется сходящейся к ,
если для любого
называется сходящейся к ,
если для любого
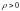 существует номер
существует номер
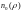 такой, что для любого номера
такой, что для любого номера
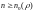 выполняется неравенство
выполняется неравенство
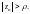
Другими словами, сходимость
последовательности к бесконечности
означает, что для любого сколь угодно
большого числа
можно найти такой номер, начиная с
которого все элементы последовательности
находятся в -окрестности
точки
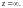 Символически это записывают так:
Символически это записывают так:
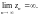
Свойства последовательности, сходящейся
к

1.
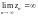 тогда и только тогда, когда
тогда и только тогда, когда
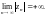
2.
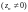 тогда и только тогда, когда
тогда и только тогда, когда
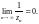
Пример 1. Пользуясь определением предела последовательности, доказать, что

Решение.
Зададим произвольное малое число
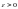 и рассмотрим -окрестность
точки
и рассмотрим -окрестность
точки
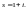 Покажем, что существует такое натуральное
число
Покажем, что существует такое натуральное
число
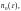 что для любого
что для любого
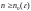 все точки рассматриваемой последовательности
будут находиться в -окрестности
точки s.
Это значит, что должно выполняться
неравенство
все точки рассматриваемой последовательности
будут находиться в -окрестности
точки s.
Это значит, что должно выполняться
неравенство
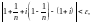
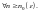
Поскольку
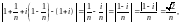
то последнее
неравенство принимает вид
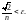 Решаем его относительно
Решаем его относительно
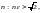
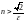 и полагаем
и полагаем
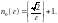 Поскольку
Поскольку
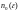 найдено, то тем самым доказано, что
предел рассматриваемой последовательности
равен
найдено, то тем самым доказано, что
предел рассматриваемой последовательности
равен
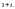
Пример 2. Найти
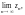 если последовательность
если последовательность
 задается формулой:
задается формулой:
1)
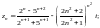 2)
2)
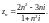
Решение. 1) Найдем отдельно пределы действительной и мнимой частей данной последовательности, что мы можем сделать, используя свойство 1) предела последовательности. По формулам (29.1) и (29.2) получаем:
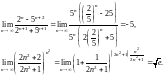
Получили, что
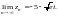
2) Запишем сначала элементы последовательности (комплексные числа) в алгебраической форме:
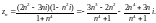
Легко убедиться,
что
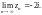
Пример 3. Найти если последовательность задается формулой:
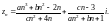
Решение.
В наших обозначениях
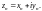 Значит,
Значит,
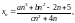
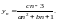
Рассмотрим различные случаи.
1. Допустим, что
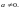 В этом случае
В этом случае
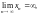
 Другими словами, для произвольного
Другими словами, для произвольного
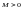 существует номер
существует номер
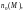 что для любого
что для любого
 справедливо
справедливо
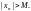 Так как
Так как
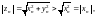 то
то
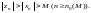 Отсюда следует, что
Отсюда следует, что
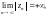 т. е.
т. е.
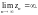
2. Пусть
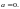 Тогда
Тогда
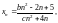
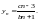
Рассмотрим далее четыре случая коэффициентов b, c.
Если
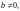
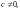 то находим:
то находим:
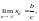
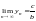 и
и
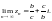
Если
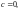 то
то
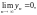
Если
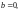 то
то
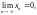
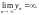
Так как
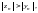 то
то
Если то
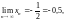
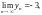
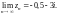
Задания
