Собственные (свободные) колебания механической системы

Колебания будем считать малыми (в уравнении Лагранжа II рода отбрасывают все слагаемые второго и более высокого порядка по обобщённым координатам и обобщённым скоростям – в этом случае колебания будут считаться линейными). Рассмотрим механическую систему, на которую наложены геометрические двусторонние идеальные связи. Составим дифференциальное уравнение на основе уравнения Лагранжа II рода.

Потенциальная энергия представляется в виде:

Выполним преобразования:

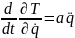
Получили обыкновенной дифференциальное уравнение II порядка, которое описывает собственные колебания механической системы.

Пример: прямолинейные колебания материальной точки.

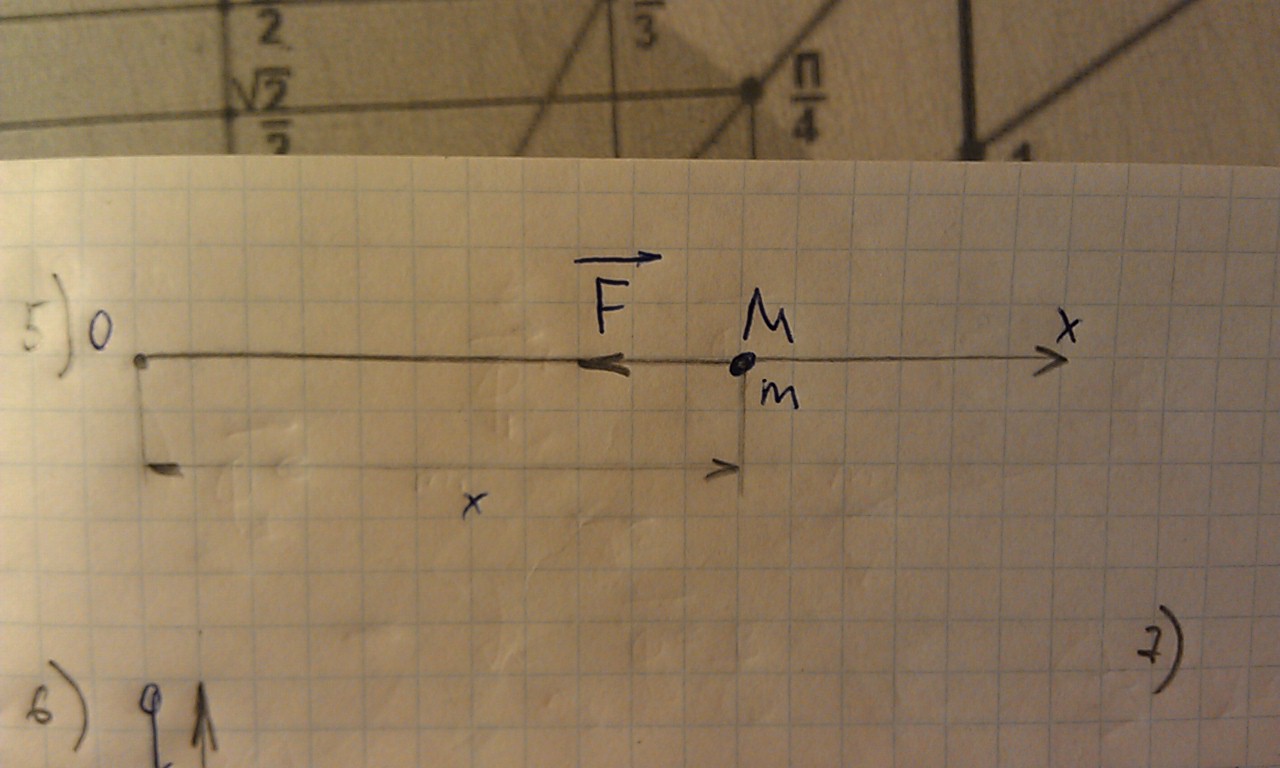
Изучаемая точка М совершает колебательные движения и стремится возвратиться в положение О (положение равновесия) под действием восстанавливающей силы F.

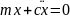
Преобразуем уравнение (1) к виду удобному для интегрирования, разделив левую часть на

Коэффициент k учитывает инерционный и жесткостные характеристики механической системы.

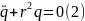
Получили однородное линейное ОДУ II порядка с постоянным коэффициентами.

Из справочника по математике известно, что решение этого уравнения имеет вид:

Выполним подстановку в уравнение (2):

Получили характеристическое уравнение.

Из справочника для этого случая находим решения

Из этого соотношения будет определена зависимость обобщённой координаты от времени.

В процессе интегрирования на двух уровнях возникли постоянные интегрирования 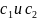, которые определяются из начальных условий . Это решение соответствует решению второй задачи динамики.

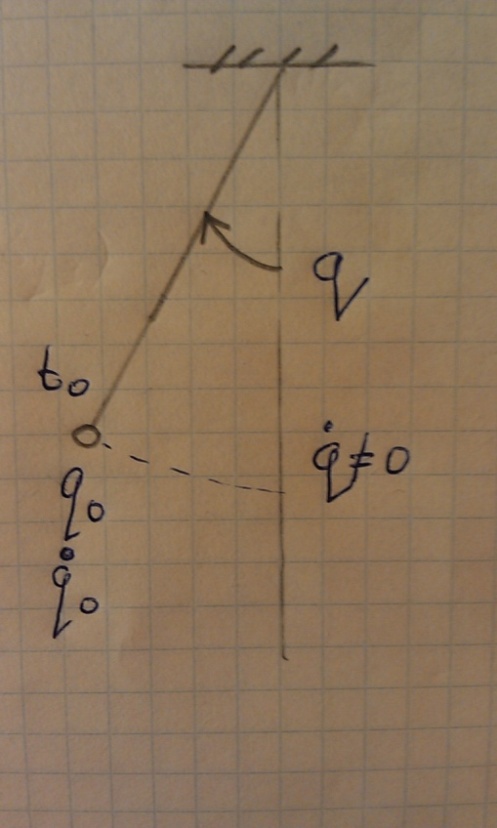
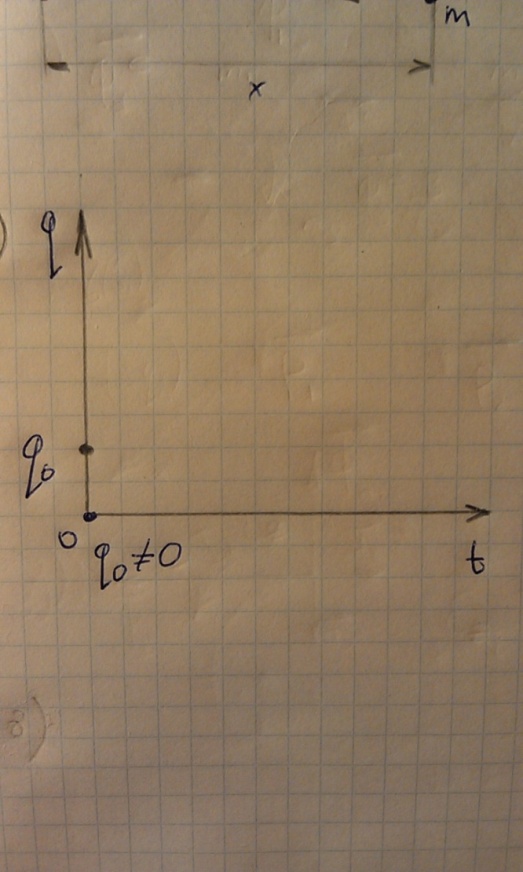
Начало графика располагается в положении , т.е. то положение, для которого началось наблюдение собственных колебаний. Возможно расположение начала графика в точке О, но при этом следует указывать, что обобщённая скорость имеет ненулевое значение.

Условием существования собственных колебаний является ненулевое значение или ненулевое значение , либо то и другое одновременно. Причины возникновения собственных колебаний не обсуждаются.