Лекция №9 Общее уравнение динамики
Рассмотрим механическую систему, состоящую из N материальных точек, на которых наложены геометрические стационарные двусторонние связи.
На основе признака Даламбера считается, что на систему действуют активные силы, реакции, силы инерции, находящиеся в состоянии равновесия в данный момент времени. Причем рассматриваем только уравнение по силам, а не по моментам.
Умножая
скалярно, получаем сумму работ всех
сил на систему, на возможные перемещения.
Эта сумма равна нулю.
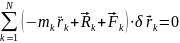
Применительно к декартовым координатам имеем:
Это выражение аналогично формуле:
Общее уравнение динамики можно выразить через обобщённые координаты . Причём суммарная элементарная работа может вычисляться для каждой обобщённой координаты по отдельности.
Пример:
Направление перемещения
выбрано условно, поскольку неизвестно,
как будет перемещаться трёхгранная
призма. На схеме изображаются силы,
которые будут выполнять работу на
возможном перемещении. Грузы
и
участвуют в сложном движении. Движение
совместно с призмой будет переносным.
Реакции связей не обозначены, поскольку
связи считаются идеальными. Все
поверхности абсолютно гладкие.
(Дополнительный вопрос:
ежели б силы разделялись на внешние и
внутренние, то горизонтальная поверхность
считалась абсолютно гладкой, а требования
к наклонным поверхностям не предъявлялись
бы.)
Составим общее уравнение динамики по всем трём перемещениям по отдельности.
На перемещении :
На перемещение
:
На перемещение
:
Уравнение Лагранжа второго рода
Эти уравнения представляют собой методику составления обыкновенных дифференциальных уравнений (ОДУ) движения механической системы путём вычисления кинетической и потенциальной энергии. Эти уравнения имеют вид:
Число уравнении соответствует числу степеней свободы механической системы.
Рассмотрим порядок приведения этих уравнений:
1) определяем частную
производную кинетической энергии по
обобщённой скорости (
.
Для этого необходимо использовать
квадратичную форму кинетической
энергии:
2) определяем производную:
Для примера прямолинейного
движения получим
3) выделяем частную производную кинетической энергии по обобщённой координате:
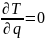
4) определяем обобщённую силу:
Практическое применение уравнения Лагранжа будет использоваться на примере теории колебаний механических систем с одной степенью свободы.
Основные понятия колебательного процесса
Колебательное движение – это движение, при котором обобщённые координаты или часть из них неоднократно принимают нулевые значения.
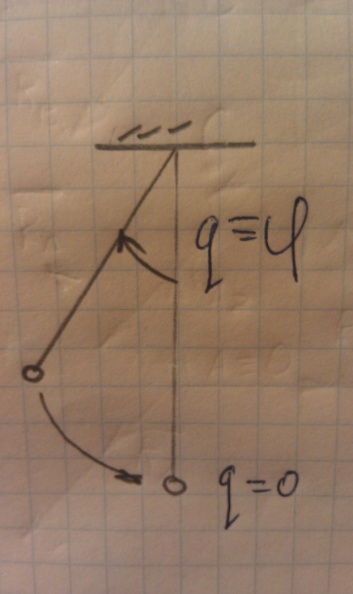
Нулевые значения q достигаются в положении равновесия механической системы.
Лекция №10
Рассмотрим различные случаи равновесия.
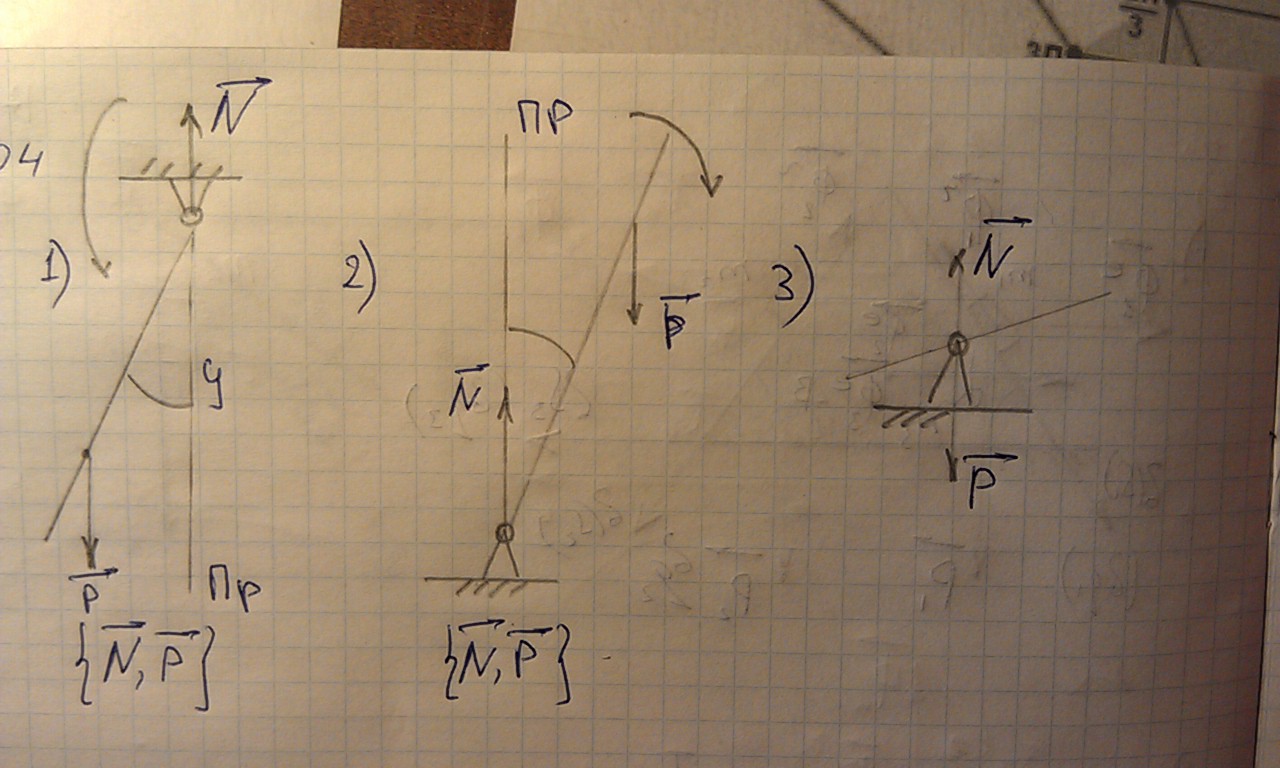
1) создаётся пара сил
,
которая возвращает систему в положение
равновесия. Это равновесие будет
устойчивым.
2) Создаётся пара , которая выводит систему из положения равновесия. Оно неустойчивое.
3) Безразличное положение равновесия.
Вывод: колебательный процесс
возможен только относительно устойчивого
положения равновесия.
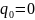
Потенциальная энергия в положении устойчивого равновесия равняется нулю.
Приведённые рассуждения позволяют сформулировать условие Лагранжа-Дирихле:
Для устойчивого положения равновесия механической системы необходимо и достаточно, чтобы потенциальная энергия системы в этом положении имела изолированный относительный минимум.
Составляющие обобщённые силы
- потенциальная составляющая,
которая учитывает действие потенциальных
сил, в том числе силу тяжести. Эта
составляющая присутствует во всех
видах колебаний в том числе она может
быть единственной.
- составляющая сопротивления,
которая зависит от обобщённой скорости
.
Рассматривается линейный участок, где сила сопротивления линейно зависит от скорости.
- возмущающая
составляющая, которая обеспечивает
передачу механической энергии системы
по какому-либо закону.