Лекция №8

Полученные выражения можно записывать на координатные оси и в проекциях на нормальную и касательную составляющую. Последний вариант учитывает естественные составляющие сил инерции: нормальную и касательную.

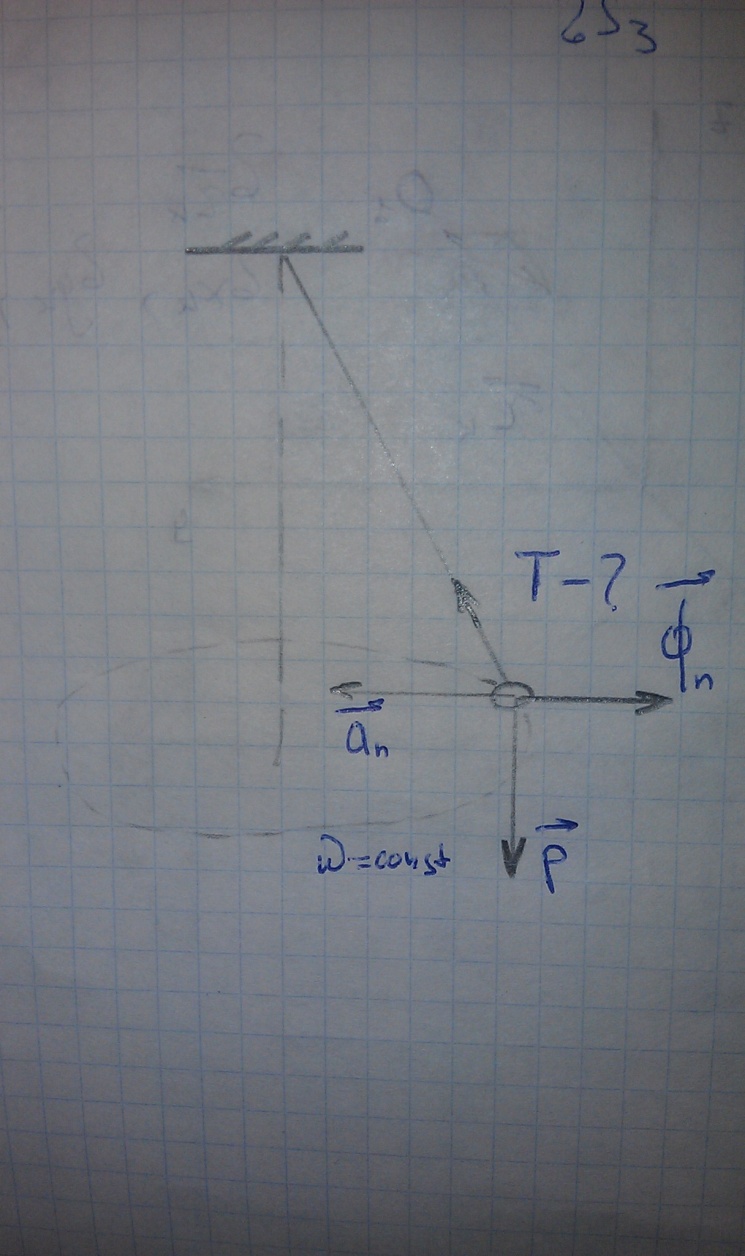
В данном примере необходимо определить силу реакции Т, т.е. решить первую задачу динамики. Для этого можно воспользоваться основным уравнением динамики, либо принципом Даламбера, для чего в рассмотрение следует ввести силу инерции .

2. Механическая система.

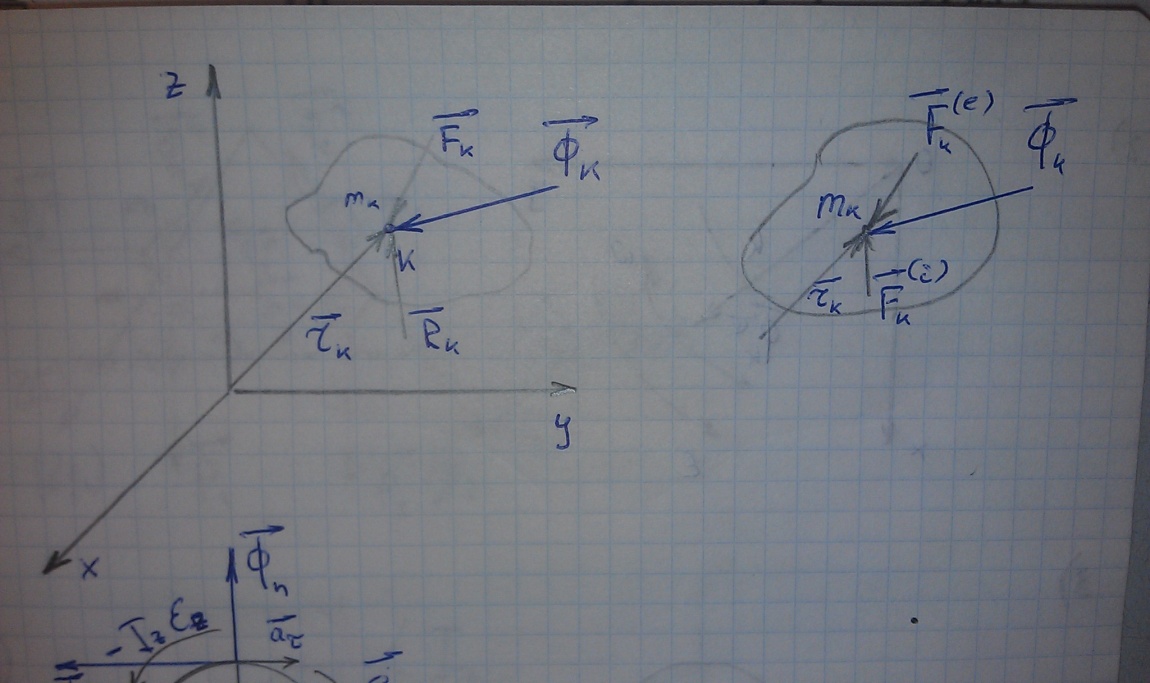
При рассмотрении сил, действующих на механическую систему можно использовать две классификации этих сил:

а)

б)

Объединять или смешивать силы по разным классификациям нельзя. Yпример, сила тяжести по первой классификации будет относиться к активным силам , по второй классификации будет относиться к внешним силам 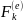. Тогда принцип Даламбера примет вид:

Для k-той точки механической системы:

или

При движении механической системы активная сила, реакция связей и сила инерции составляют равновесную систему сил для каждой точки механической системы в данный момент времени.

По второй классификации равновесную систему сил образуют внешние, внутренние силы и силы инерции.

Составим систему уравнений в соответствии с принципом Даламбера для механической системы:

В проекциях на координатные оси образуется 6 уравнений равновесия для данного момента времени. Полученное число уравнений согласуется с уравнениями равновесия статики, которых также 6, но в них отсутствуют силы инерции. Можно составить вторую систему уравнений равновесия на основе второй классификации.

Известно, что главный вектор и главный момент внутренних сил в большинстве задач можно принять равным нулю.

Для решения полученной системы уравнений, которой используется в классификации по внешним и внутренним силам необходимо знать:

1) точку приложения суммарной силы инерции для механической системы;

2) значения суммарного момента сил инерции, как по величине, так и по направлению.

Для ответа на первый вопрос необходимо сопоставить систему уравнений равновесия с теоремой об изменении количества движения.

Сопоставим это уравнение с первым уравнением системы. Получаем:

Это означает, что вектор суммарной силы инерции механической системы следует изображать приложенным в центре масс этой системы. Для определения суммарного момента сил инерции необходимо сопоставить систему уравнений с теоремой об изменении кинетического момента.

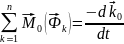
Практически рассматривается проекция данного соотношения на ось вращения.

Известно:

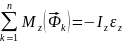
Момент силы инерции в проекции на координатную ось z (ось вращения) равен произведению момента инерции механической системы и углового ускорения относительно той же самой оси вращения, взятому с обратным знаком.

Дополнительный вопрос: какая из составляющих сил инерции участвует в создании момента этих сил относительно оси вращения.

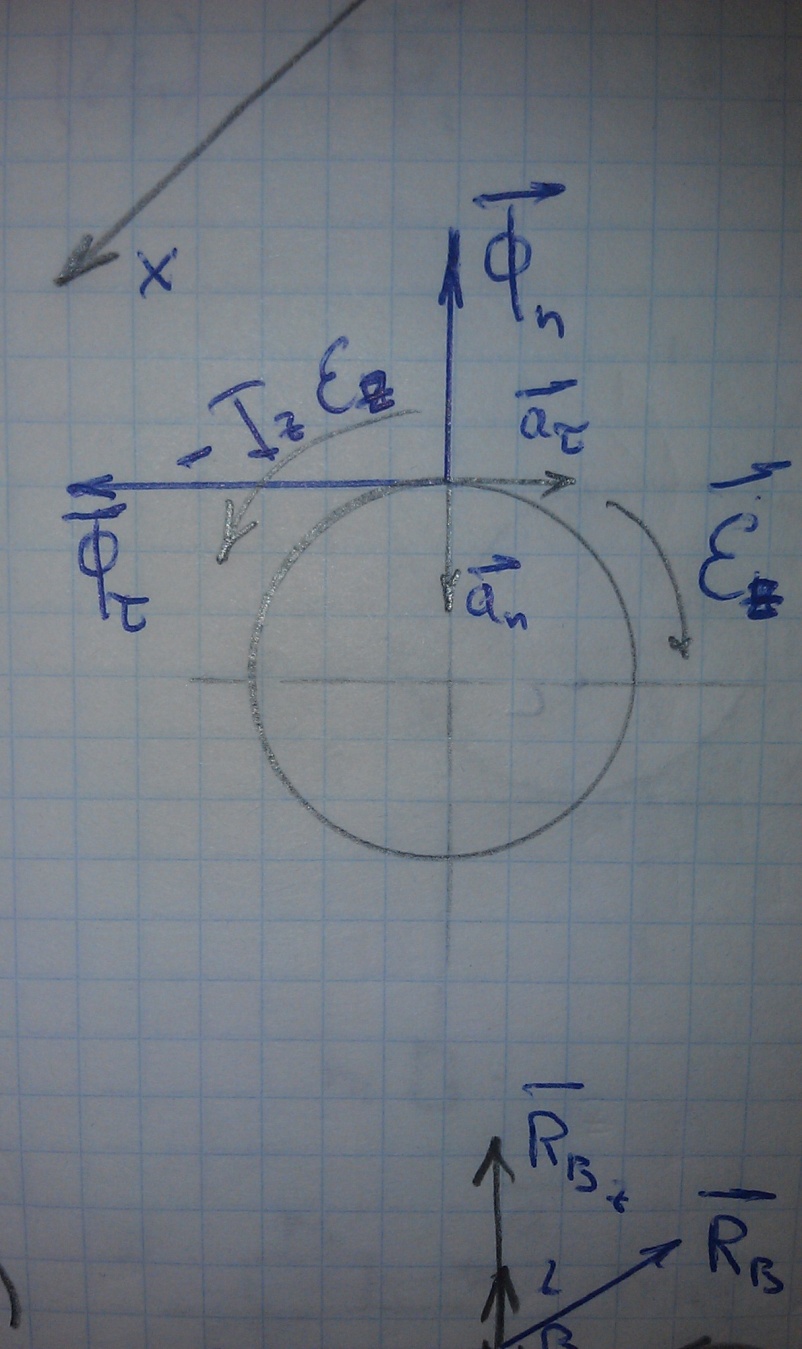
Касательная составляющая создаёт момент силы вращения.

Выполним сопоставление системы уравнений с теоремой об изменении кинетической энергии. Это необходимо для определения работы силы инерции.

Дифференциальная форма:

Вывод: суммарная работа сил инерции на каком-либо перемещении механической системы равна изменению кинетической энергии системы на этом же перемещении, взятому с обратным знаком.

Динамические реакции опор твёрдого тела, вращающегося вокруг неподвижной оси (10.04)

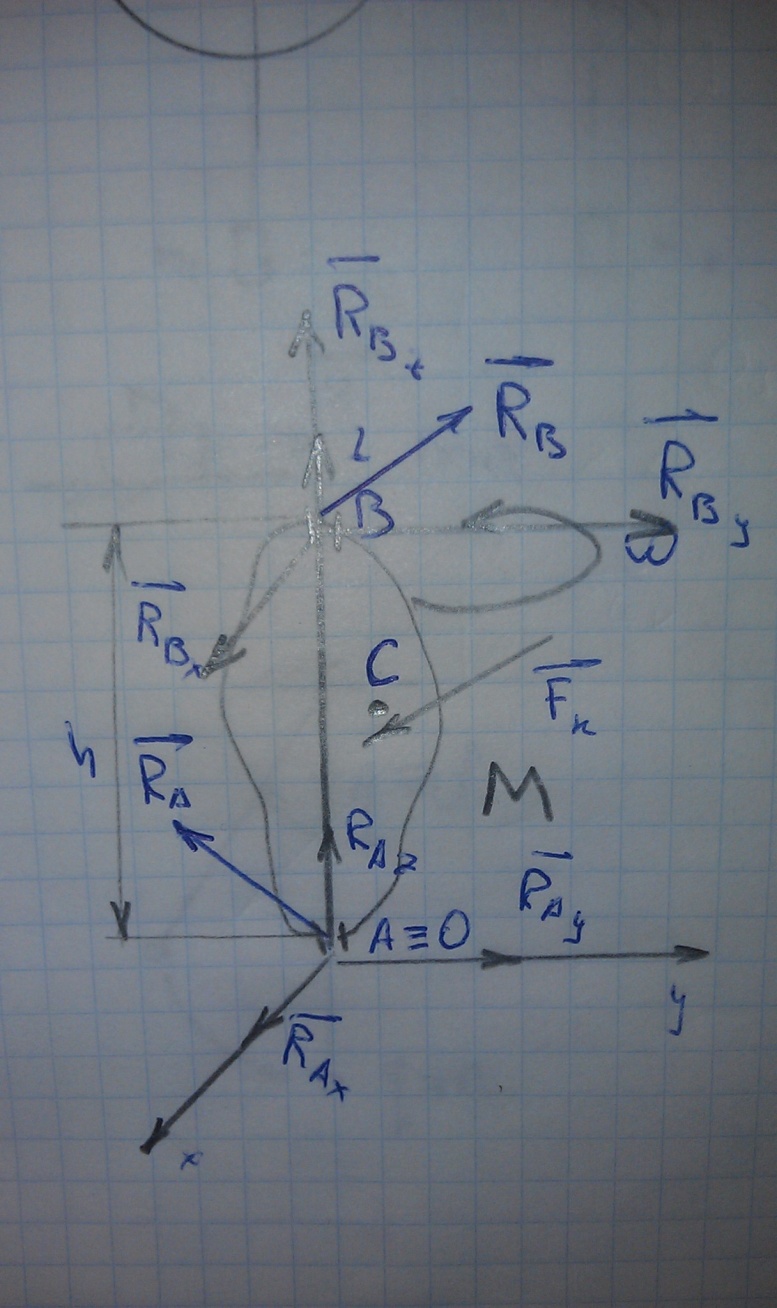
На изучаемое тело действуют активные силы, в результате чего возникают реакции в опорах А и В. Их составляющие , 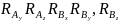необходимо определить, что возможно на основе принципа Даламбера. Введём в рассмотрение силы инерции.

Определим составляющие сил инерции и составляющие моментов сил инерции по координатным осям.

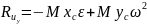
Составим уравнение равновесия твёрдого тела в данный момент времени:

Где

Где

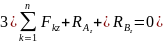
Рассмотрим особенности полученных уравнений:

а) составляющие реакции опор отделены друг от друга, это вертикальные составляющие и , и группа составляющих 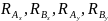. Причём первые две составляющие от сил инерции не зависят. определяются суммарно по уравнению 3.

б) уравнение №6 не включает в себя реакций опор и преобразуются в дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси ( ) .

Получаем, что для определения составляющих 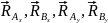следует использовать уравнение №1, №2, №4 и №5, которые образуют систему алгебраических уравнений. Большое значение имеет момент, образованный и , который может привести к разрушению нижней опоры. Поэтому следует уменьшать расстояние h.

в) силы инерции проявляют своё действие, ежели центр тяжести не находится на оси вращения . В этом случае силы инерции влияют на величину и направление реакций опор. К статической составляющей добавляется динамическая. Для того чтобы центр тяжести находился на очи вращения требуется статическая балансировка тела.

На противоположной стороне укрепляются дополнительные грузы, после чего центр тяжести возвращается в геометрический центр (точку О). В этом случае динамическая составляющая реакций опор становится нулевой.

Кроме статической балансировки существует динамическая балансировка. Эта операция производится на специальных балансировочных станках.