Потенциальная энергия

Понятие потенциальной энергии рассматривается на основе работы силы тяжести.

Потенциальная энергия равна работе, совершённой силой тяжести при её перемещении из положения 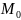в положение М, взятая с обратным знаком.

Рассматривая потенциальную энергию в сочетании с кинетической, получаем механическую энергию:

Рассмотрим закон сохранения механической энергии:

Ежели рассматривать действие только силы тяжести, то закон сохранения механической энергии будет выполняться. Силы тяжести относятся к категории потенциальных сил.

Сила будет считаться потенциальной, ежели она зависит только от координаты точек пространства, к этим силам относится сила упругости и сила тяжести. Ежели силы зависят от других параметров, то они являются непотенциальными, например это силы сопротивления, в частности сила трения – они зависят от скорости. Существуют различные зависимости силы сопротивления от скорости.

В случае действия непотенциальных сил закон сохранения механической энергии не выполняется:

В этом случае часть механической энергии безвозвратно преобразуется в тепловую.

Аналитическая механика Основные понятия аналитической механики

Аналитическая механика устанавливает общие связи и методы изучения равновесия и движения механических систем. В это разделе изучаются общие уравнения, позволяющее не разделять статику и динамику.

Рассмотрим связи в аналитической механике.

Эти связи зависят от координат точек пространства и эти связи называют геометрическими. Кроме того, существуют связи, которые зависят от кинематических параметров.

Такие связи называются кинематические.

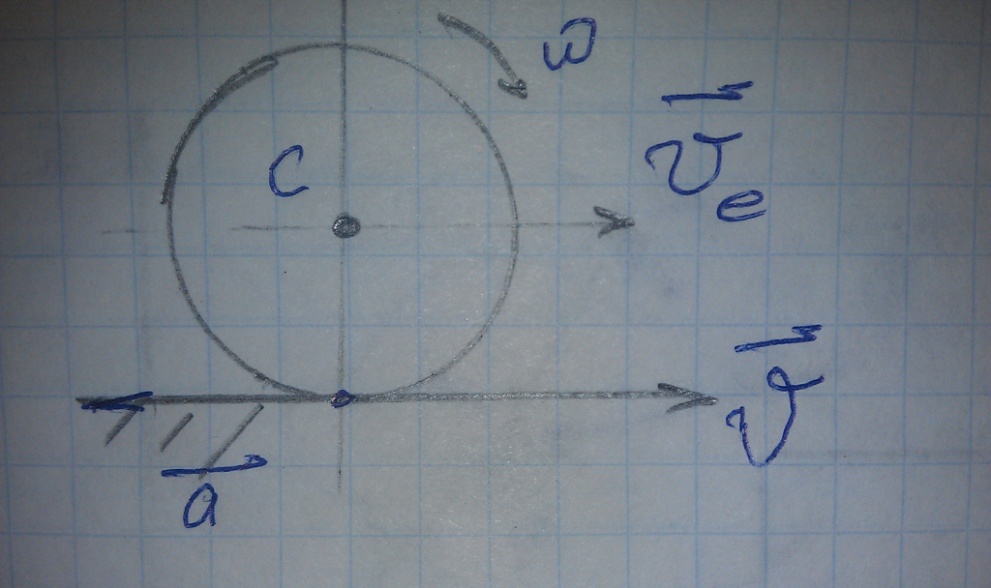
Кроме того, связи могут быть нестационарными (зависящие от времени t) и стационарными. Связи могут оказаться односторонними (изучаемая точка находится на какой-либо поверхности и имеет возможность покинуть эту поверхность в том или ином направлении).

Будут изучаться геометрические, стационарные, двухсторонние связи.

Введём понятие обобщённой координаты. Вводятся любые геометрические характеристики в виде декартовых координат, углов поворота, полярных координат и т.д. Каждая обобщённая координата обозначается , I – степень свободы: . Число обобщённых координат соответствует числу степеней свободы системы.

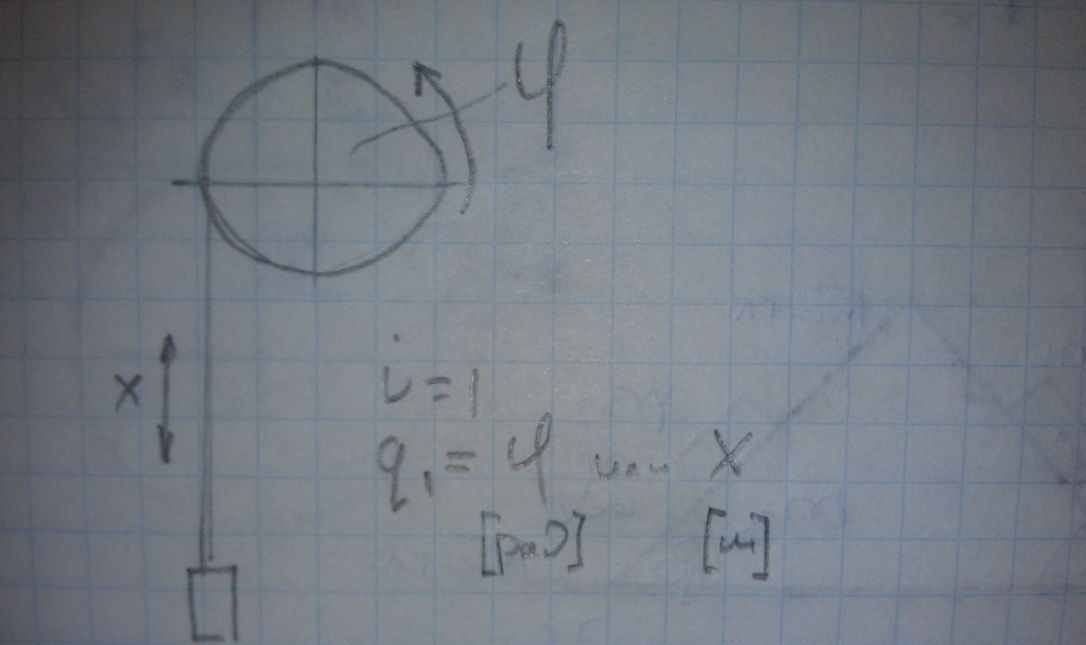
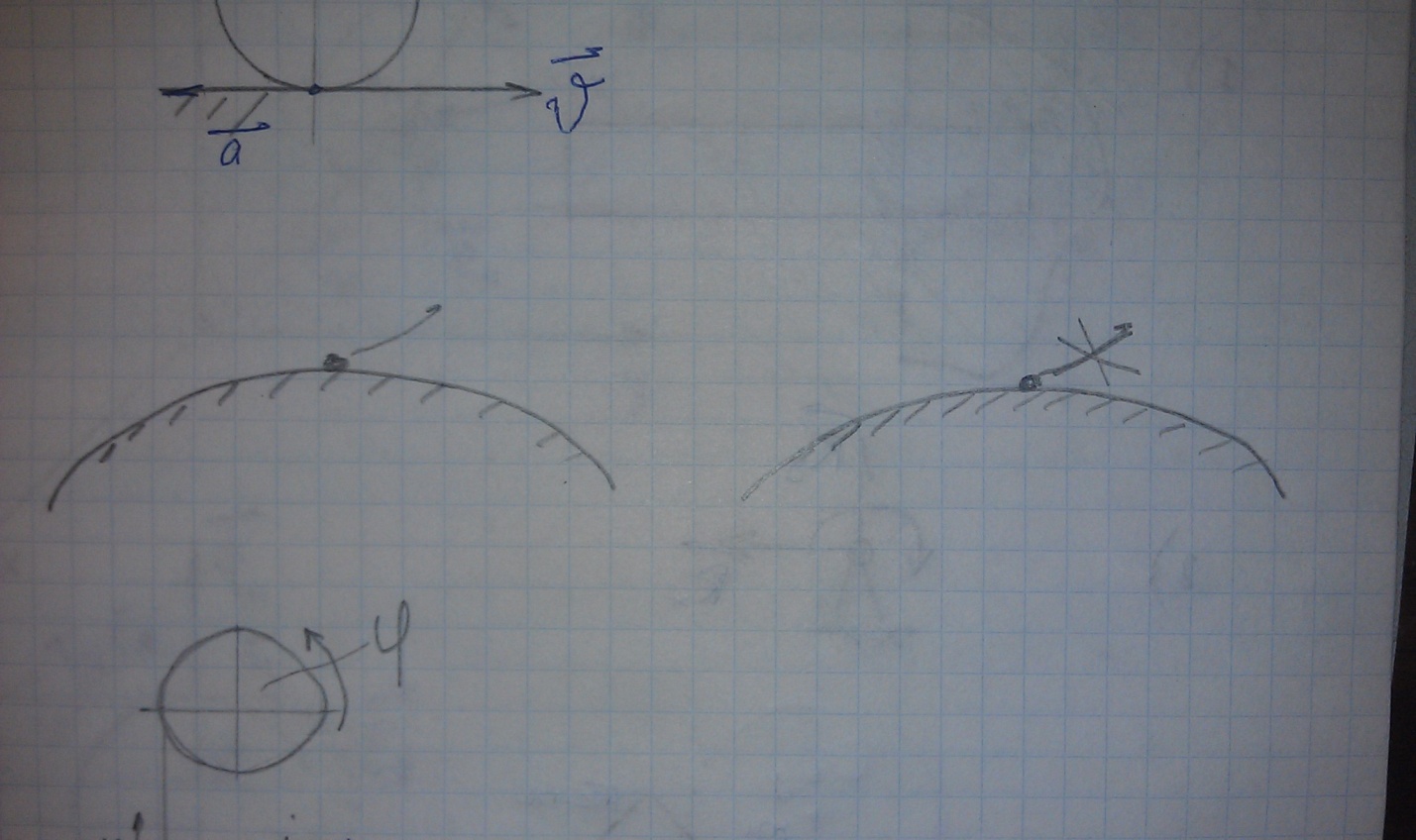
Введём понятие возможных перемещений.

Выбирается предполагаемое положение равновесия, и, с учётом наложенных связей определяются возможные изменения координат точки .

Лекция №7

Возможные перемещения

Одно из этих перемещением окажется действительным и будет обозначено 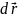причём это перемещение произойдёт за время . На возможном перемещении будет выполнятся возможная элементарная работа за счёт силы F.

Обобщённые силы

Необходимость введения в рассмотрение понятие обобщённой силы связано с тем, что обобщённой координате необходимо сопоставить аналог силы способный рассчитать работу силы через обобщённые координаты. При расчёте работы, которая является скалярной величиной, необходимо при обобщённой координате иметь коэффициент, который является скалярной величиной и может измеряться в [Н] или [Н*м]. Таким коэффициентом и будет являться обобщённая сила . Тогда суммарная элементарная работа на возможных перемещениях будет определяться:

Суммирование выполняется по числу степеней свободы, а не по числу материальных точек, как это было при рассмотрении активных сил и реакций связи.

1. Обобщённая сила – скалярная величина.

2. Каждой обобщённой силе соответствует своя обобщённая координата и своя степень свободы.

3. Размерность обобщённой силы зависит от размерности обобщённой координаты таким образом, чтобы произведение этих величин имело размерность [Дж].

Б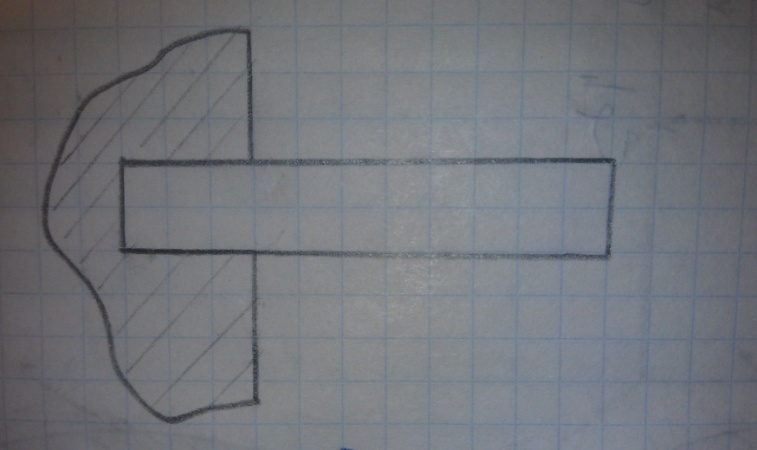 ыла рассмотрена суммарная элементарная работа на возможных перемещениях под действием активной силы F. Работа реакций связей не учитывалась, это справедливо для геометрических связей, для которых:

Это равенство справедливо, поскольку возможных перемещений для жёсткой заделки не имеется.

Такие связи, в которых суммарная элементарная работа реакций связей на возможных перемещениях равна нулю, называются идеальными. Таким образом, получаем окончательную формулировку связей в соответствии с их классификацией. Имеем геометрическую, стационарную, двустороннюю, идеальную связь. (Когда связь считается идеальной?) При решении задач число уравнений движения равняется числу степеней свободы системы, при чём можно рассматривать по отдельности каждое перемещение.

Пример:

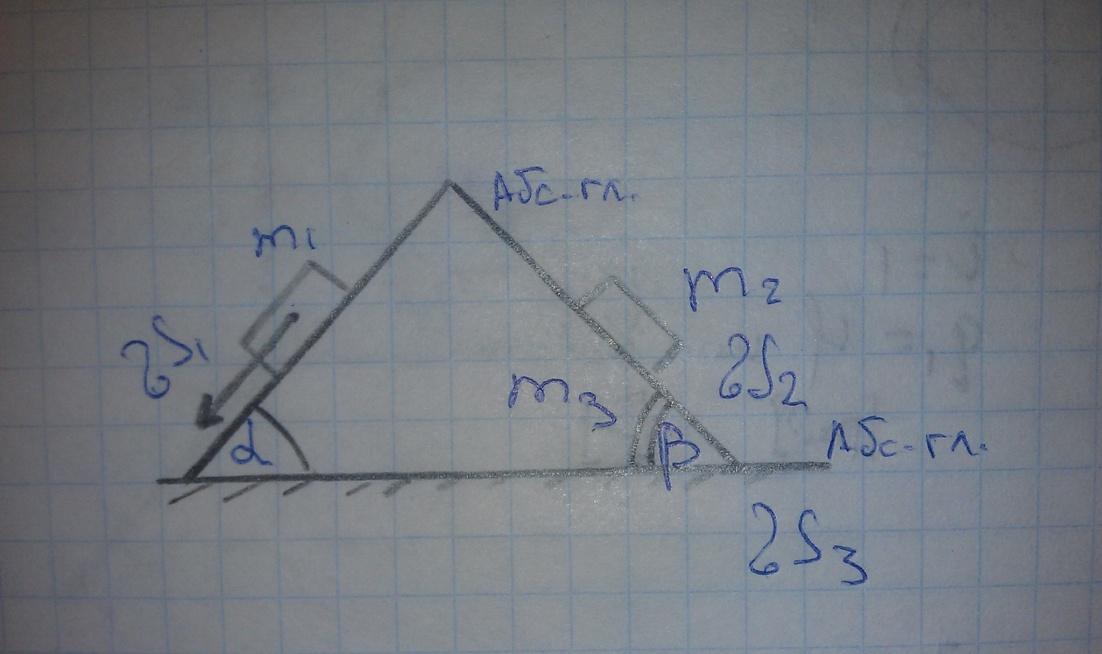
Имеем призму, способную перемещаться по горизонтальной плоскости без трения. Для механической системы имеем три возможных перемещения, которые заданы естественным способом задания движения: . Имеем три степени свободы i=3, и три обобщённые координаты, заданные через .

Принцип возможных перемещений

Принцип регламентирует условие равновесия точки или системы.

Для равновесия материальной точки или механической системы, находящихся под действием активных сил и подчинённых геометрическим, стационарным, двусторонним идеальным связям, необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении из предполагаемого положения равновесия равнялось нолю. В определении отсутствует реакции связи, потому что связи идеальны. Математическая формулировка:

Ежели связь будет неидеальной, получаем .

В обобщённых координатах: . Левые части этих уравнений представляют собой суммарную элементарную работу сил на возможных перемещениях.

Принцип Д’Аламбера

1. Материальная точка.

Известно основное уравнение динамики: (свободная точка). Силы F включают в себя как активные силы, так и реакции связей, т.е. в полном виде: 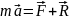(точка со связями). - принцип Даламбера.

При движении материальной точки активные силы, реакции связей и силы инерции образуют равновесную систему сил в данный момент времени.