Лекция №5 Дифференциальное уравнение плоского движения твёрдого тела

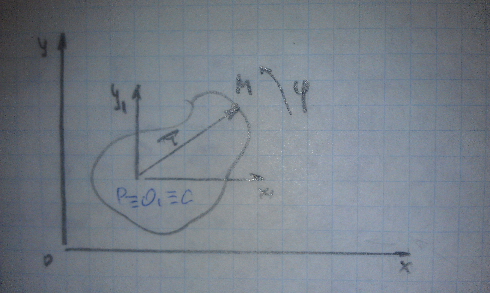
В отличие от кинематики в точке О₁ будет располагаться центр тяжести твёрдого тела, поэтому право свободного выбора полюса будет утрачено. Воспользуемся теоремой о движении центра масс механической системы, которая позволяет составить дифференциальные уравнения переносной составляющей.

Рассмотрим относительное движение, используя теорему об изменении кинетического момента:

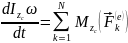
Момент инерции вычисляется относительно оси проходящей через точку С, поэтому любое изменение положения оси z потребует пересчёта момента инерции.

Рассмотренные дифференциальные уравнения поступательного, вращательного и плоского движений позволяют решать как первую, так и вторую задачи динамики.

Теорема об изменении кинетической энергии

1) Работа силы

Рассматривается элементарная работа dA, сила F на элементарном перемещении ds.

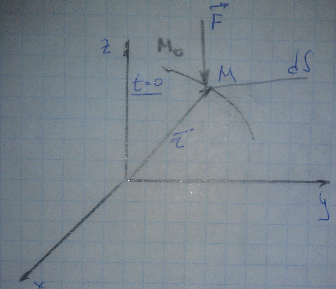
Элементарную работу можно определить:

(естественный способ задания движения точки)

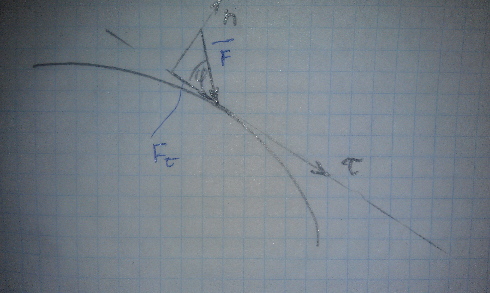
Работа – это скалярная величина, знак которой определяется знаком проекции силы .

Частные случаи:

1)

2)

3)

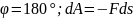
Имеется возможность выразить элементарную работу, используя векторный способ задания движения точки.

Из естественного способа задания движения точки известно .

Элементарная работа определиться:

Воспользуемся координатным способом задания движения точки:

Работа силы F на перемещение определяется интегрированием элементарных работ.

Рассмотрим понятие мощности силы. Мощность силы – это работа. Которая совершается силой в единицу времени: 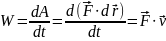. Мощность машины W может быть употреблена либо воссозданием большого усилия , либо достижением высокой скорости .

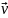Рассмотрим частные случаи определения работы силы на примере силы тяжести.

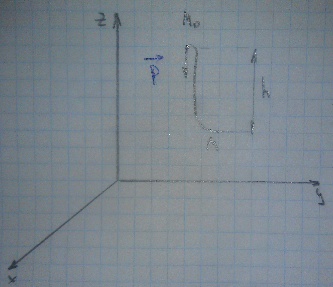
Вычислим работу силы тяжести на перемещение :

Становится очевидным, что работа силы тяжести не зависит от траектории движения изучаемой точки, а зависит только от изменения координаты z, т.е. величины h. При падении вниз работа имеет знак «+»: .

Рассмотрим работу силы при вращении твёрдого тела на неподвижной оси.

Используя векторный способ задания движения точки, определяем

Выполним круговую перестановку сомножителей:

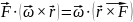, где

, где

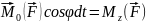
Мощность силы при вращательном движении определится:

При определённом значении мощности машины эта мощность может быть направлена на создание вращательного момента либо на развитие угловой скорости.

Лекция №6 Кинетическая энергия

Для материальной точки:

Для механической системы выполняется суммирование:

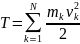
Рассмотрим кинетическую энергию сложного движения.

Теорема Кёнига:

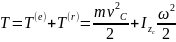
Для поступательного движения известно .

Для вращательного движения

3. Теорема об изменении кинетической энергии

Рассмотрим материальную точку.

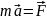
– теорема об изменении кинетической энергии в дифференциальной форме

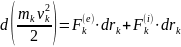
Выполняем суммирование:

Изменение кинетической энергии механической системы при её перемещении из одного положения в другое равно сумме работ внешних и внутренних сил на соответствующее перемещение точек системы. Для абсолютно твёрдого тела суммарная работа внутренних сил равна нулю.

Работа силы инерции определяется следующим образом:

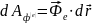
Работа силы Кориолиса равна нулю, поскольку эта сила перпендикулярна вектору относительной скорости.