Лекция №4 Теорема о движении центра масс механической системы

Теорема справедлива для изучения изменяемых механических систем. Необходимо различать понятие центра тяжести элементов механической системы и центра масс механической системы.

Центр масс МС движется также, как и материальная точка, масса которой такая же как и у всей МС.

Используем теорему об изменении количества движения:

В проекциях на координатные оси:

Существует следствия из этой теоремы, которые регламентируют частные случаи движения центра масс. В том числе и для нахождения этой точки в состоянии покоя.

Следствие №1

Ежели главный вектор внешних сил, действующих на МС, равен 0, то вектор скорости центра масс постоянен по величине и направлению.

Следствие №2

Ежели проекция главного вектора на какую-либо координатную ось равна 0, то проекция скорости на эту ось – величина постоянная.

Вывод из следствий:

Центр масс будет двигаться прямолинейно и равномерно или находится в состоянии покоя.

Пример: МС «Призма №1 – призма №2»

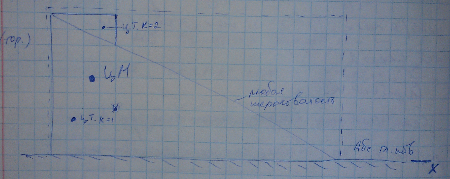
Поверхность должна быть абсолютно гладкой, т.к. в другом случае возникли бы силы трения, которые относятся к внешним силам. Наклон поверхности может быть любой т.к. сила трения относится к внутренним.

Используем следствия №2 для оси OX:

- прямолинейное равномерное движение.

Из начальных условий известно, что t=0, – обе призмы были неподвижны. Следовательно, положения центра масс не изменится по оси OX, т.к. отсутствуют внешние силы, способные вывести его из состояния покоя.

Для поступательного движения твёрдого тела используется теорема о движении центра масс и учитывается, что все точки твёрдого тела двигаются так же, как и центр масс.

Теорема об изменении кинетического момента.

В начале рассмотрим понятие момента количества движения для материальной точки.

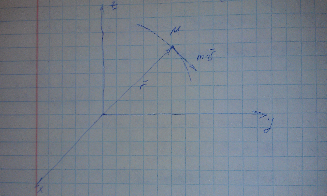
В этом случае необходимо новое понятие – момент количества движения.

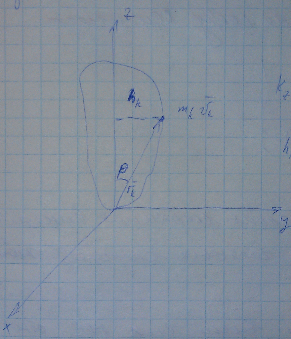
Сопоставим по аналогии понятие момента количества движения с понятием векторного момента силы относительно центра (вместо появится ). Для механической системы вводится понятие кинетического момента. Главный вектор кинетического момента: . На практике наибольшее значение имеет проекция M_z, где z – ось вращения.

, где

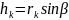
Теорема:

Первая производная по времени от кинетического момента механической системы, относительно какого-либо центра, равна векторной сумме моментов внешних сил, действующих на эту механическую систему, относительно того же центра.

В проекциях на координатную ось:

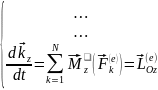
Рассмотрим законы сохранения кинетического момента как частный случай этой теоремы. Ежели главный момент внешних сил МС, относительно какого-либо центра равен 0, то вектор кинетического момента системы относительно того же центра будет постоянен как по величине, так и по направлению:

Ежели проекция главного момента внешних сил на какую-либо координатную ось равна 0, то величина проекции кинетического момента на ту же ось – величина постоянная.

Рассмотрим два положения: обороты увеличения II, обороты уменьшения I.

Этот закон применим для изменяемых МС.

Дифференциальные уравнения вращательного движения твёрдого тела вокруг неподвижной оси:

Используя теорему об изменении кинетического момента в проекции на ось z:

Обратим внимание, что реакции опор R_A и R_B являются внешними силами, но момента относительно оси вращения они не создают, поэтому по ни теорема ни дифференциальные уравнения вращательного движения не позволяют рассчитать эти реакции. Это возможно с применением принципа Даламбера – I задача динамики.

Рассмотрим частные случаи:

1. К твёрдому телу прикладывается постоянный момент относительно оси вращения. Тело будет вращаться либо ускоренно, либо будет тормозить.

2. Момент внешних сил относительно оси вращения равен 0. Тело будет вращаться с постоянной частотой (эксплуатационный режим работы).