термехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермехтермех

Теоретическая механика Конспект лекций, 3 семестр 2013г. Поздеев Е.Д., гр. С11-АЭ

Оглавление

Динамика 3

Лекция №1 3

Дифференциальное уравнение движения материальной точки 4

Две основные задачи динамики материальной точки 5

Лекция №2 7

Динамика относительного движения материальной точки 7

Дифференциальные уравнения движения механической системы 9

Лекция №3 9

Лекция №4 11

Теорема о движении центра масс механической системы 11

Лекция №5 16

Дифференциальное уравнение плоского движения твёрдого тела 16

Лекция №6 19

Потенциальная энергия 20

Аналитическая механика 21

Основные понятия аналитической механики 21

Лекция №7 23

Лекция №8 25

Лекция №9 30

Уравнение Лагранжа второго рода 31

Основные понятия колебательного процесса 32

Лекция №10 33

Собственные (свободные) колебания механической системы 34

Динамика Лекция №1

Динамика – раздел теоретической механики, в котором изучается движение механических объектов (материальных точек), а также механические системы в их взаимодействии с силовыми факторами (силами и моментами), которые эти действия вызывают.

Основные законы динамики сформулированы Ньютоном.

Аксиомы динамики:

1) Первая аксиома динамики распространяет действие первого закона Ньютона на инерциальные системы отсчёта:

Всякая изолированная материальная точка (т.е. точка, не подверженная воздействию каких-либо тел – силовым воздействиям) находится в состоянии равномерного прямолинейного движения или в состоянии покоя по отношению к любой неподвижной системе отсчёта.

Инерциальные системы отсчёта – это такие системы, которые либо неподвижны, либо находятся в состоянии равномерного прямолинейного движения, т.е. инерциальном состоянии.

Всякая изолированная материальная точка находится в состоянии равномерного прямолинейного движения, либо покоя.

2) Ускорение материальной точки прямо пропорционально силе, действиующей на эту точку и обратно пропорционально массе этой материальной точки ( ).

Масса материальной точки – основная мера инерционных свойств материальной точки.

Инертность – способность сохранять параметры и направление своего движения после снятия сил, его вызвавших.

3) Все тела взаимодействуют с силами равными по модулю и противоположными по направлению.

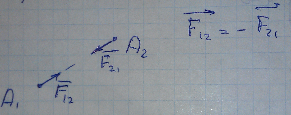
4) Принцип независимости действия сил:

Ежели на точку действует система сил, то эффект действия этой системы сил равен сумме эффектов, которые имела точка, ежели бы каждая из этих сил действовала бы на неё отдельно независимо от других.

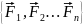
– основное уравнение динамики материальной точки

Дифференциальное уравнение движения материальной точки

Дифференциальное уравнение движения получается на основании законов движения материальной точки известных из раздела «Кинематика».

1. Дифференциальное уравнение движения в векторной форме:

2. Дифференциальное уравнение движения в координатной форме:

Проецируя основное уравнение динамики на оси координат и подставляя зависимости, получим:

3. Дифференциальное уравнение движения в естественной форме.

– бинормаль, направленная таким образом, чтобы тройка векторов образовывала правую тройку векторов. Данная система в общем случае не является инерциальной. В кинематике установлено, что ускорение точки находится в соприкасающейся плоскости траектории ( и, следовательно, не даёт проекции на бинормаль .

Две основные задачи динамики материальной точки

Основное уравнение динамики и дифференциальные уравнения движения в векторной, координатной и естественной формах позволяют решать две основные задачи динамики материальной точки:

1. По заданной массе m материальной точки и известному закону движения требуется определить силу, действующую на точку. По дифференциальным уравнениям определяется проекция равнодействующей на оси координат путём двойного дифференцирования.

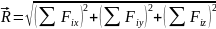
2. По заданной массе и силе действия на неё требуется определить закон движения, а так же траекторию.

Решение этой задачи осуществляется путём интегрирования дифференциального уравнения II порядка. При этом необходимо учитывать функциональные зависимости равнодействующей от координат времени скоростей. Например, при движении тела в воздухе сила сопротивления движению пропорциональна скорости движения до , при сила пропорциональна .

Таким образом в общем случае проекции равнодействующей на оси координат точки является функцией от координаты скорости.

Представим дифференциальное уравнение движения:

Известно, что одно дифференциальное уравнение движения содержит две постоянных интегрирования, поэтому для системы трёх уравнений (1) таких постоянных будет 6, поэтому (1) необходимо дополнить начальными условиями по времени , а именно задать начальное положение и начальную скорость точки: .