
- •События
- •Вычисление вероятности по классической формуле
- •Теоремы сложения и умножения вероятностей
- •Формула полной вероятности. Формула бейеса
- •Повторные испытания. Формула бернулли
- •Случайная величина и ее числовые характеристики
- •Некоторые распределения дискретных случайных величин
- •Некоторые распределения непрерывных случайных величин
- •Функция одного случайного аргумента
- •Дискретная случайная величина X задана законом распределения
- •Предельные теоремы теории вероятностей
- •Задания для домашних контрольных работ Формулы сложения и умножения вероятностей
- •Формула полной вероятности и формулы Байеса
- •Формула Бернулли
- •Случайные величины
- •Законы распределения случайных величин
Случайные величины
V. Дискретные случайные величины
Вар |
Задача (дискретные случайные величины) |
1, 12, 23 |
Стрелок может выбить 10, 9 или 8 очков с вероятностями p1, p2, p3. Количество выбитых очков – случайная величина, математическое ожидание которой равно 9,2, а дисперсия 0,36. Найти вероятности p1, p2, p3.
|
2, 13, 24 |
Случайная величина может принимать два значения х1 и х2 с вероятностями 0,6 и 0,4. Найти значения х1 и х2, если известно, что математическое ожидание случайной величины равно 24, дисперсия равна 0,24 и х1+х2<5,5.
|
3, 14, 25 |
Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1< x2. Вероятность того, что Х примет значение x1, равна 0,2. Найти закон распределения случайной величины Х, если ее математическое ожидание М(Х)=2,6 и среднее квадратическое отклонение (Х)=0,8.
|
4, 15, 26 |
Дискретная случайная величина Х имеет только три возможных значения: x1=1, x2 и x3, причем x1< x2 < x3 . Вероятности того, что Х примет значение x1 и x3 соответственно равны 0,3 и 0,2. Найти закон распределения случайной величины Х, если ее математическое ожидание М(Х)=2,2 и дисперсия D(Х)=0,76.
|
5, 16, 27 |
Известно, что случайная величина может принимать значения 1, 2, 3. Определить вероятности этих значений, если математическое ожидание случайной величины равно М(Х)=1,8 а дисперсия D(Х)=0,56.
|
6, 17, 28 |
Известно, что случайная величина может принимать значения 0, 1, 2. Определить вероятности этих значений, если математическое ожидание случайной величины равно М(Х)=0,9 а дисперсия D(Х)=0,69.
|
7, 18, 29 |
Известно, что случайная величина может принимать значения 2 и 4. Определить вероятности этих значений, если математическое ожидание случайной величины равно М(Х)=3,4 а дисперсия D(Х)=0,84.
|
8, 19, 30 |
Случайная величина может принимать два значения х1 и х2 с вероятностями 0,8 и 0,2. Найти значения х1 и х2, если известно, что математическое ожидание случайной величины равно 3,2, дисперсия равна 0,16.
|
9, 20, 31 |
Случайная величина может принимать три возможных значения: х1=4 с вероятностью p1=0,5 ,х2=6 с вероятностью p2=0,3 и х3 с вероятностями p3. Найти значения х3 и p3, если известно, что математическое ожидание случайной величины равно 8.
|
10, 21, 32 |
Случайная величина может принимать три возможных значения: х1=-1 ,х2=0 и х3=1. Найти вероятности этих значений p1, p2, p3, если известно, что математическое ожидание случайной величины равно М(Х)=0,1, а М(Х2)=0,9.
|
11, 22, 33 |
Случайная величина может принимать три возможных значения: х1=1 ,х2=2 и х3=3. Найти вероятности этих значений p1, p2, p3, если известно, что математическое ожидание случайной величины равно М(Х)=2,3, а М(Х2)=5,9.
|
VI. Задана непрерывная случайная величина Х своей плотностью распределения вероятностей f(x). Требуется:
определить коэффициент А;
найти функцию распределения F(x);
схематично построить графики функций f(x) и F(x);
вычислить математическое ожидание и дисперсию Х;
вычислить моду и медиану;
определить вероятность того, что случайная величина Х примет значение из интервала (a,b).
вариант |
f(x) |
вариант |
f(x) |
1 |
a=0 , b= /2 |
11 |
a=0 , b= 1/3 |
2 |
|
12 |
a=1/3 , b= 1 |
3 |
a=0 , b= 1 |
13 |
|
4 |
a=0 , b= 1 |
14 |
a=1 , b= 1,5 |
5 |
|
15 |
a=0 , b= 1 |
6 |
a=1 , b= 2 |
16 |
|
7 |
|
17 |
|
8 |
|
18 |
|
9 |
|
19 |
|
10 |
a=2 , b= 7 |
20 |
|



 a=1
, b=
1,5
a=1
, b=
1,5

 a=0
,
b=
3
a=0
,
b=
3

 a=0
, b=
1
a=0
, b=
1

 a=0
,
b=
1
a=0
,
b=
1 a=2
,
b=
3
a=2
,
b=
3 a=-
/4
,
b=
0
a=-
/4
,
b=
0 a=-1
,
b=
1
a=-1
,
b=
1 a=0
,
b=
1
a=0
,
b=
1 a=1
,
b=
2
a=1
,
b=
2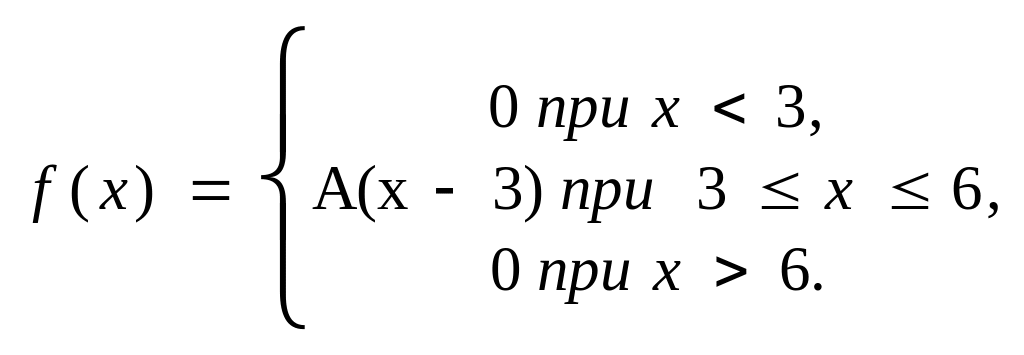 a=4
,
b=
5
a=4
,
b=
5
 a=0
,
b=
1
a=0
,
b=
1