2.4 Расчёт и построение статических характеристик замкнутой системы

Для расчета характеристик в замкнутой системе необходимо определить координаты двух точек, через которые должна пройти механическая характери­стика пониженной скорости, исходя из требований предъявляемых к рассматри­ваемому электроприводу и статическом перепаде не более 10%, при изменении нагрузки от 0 до М_ном .

Скорость пониженной характеристики при М = 0:

_{0_пон} = 14 c^-1

Координаты первой точки:

M₁ = 0; ₁ = _{0_пон}

Скорость пониженной характеристики при М =М_н, исходя из статического перепада 10%;

₂ = _{0_пон} – 0,1w_{0_пон}= 14-1,4 = 12,6 c^-1

Координаты второй точки:

M₂ = M_ном;

Расчет статической механической характеристики ЭП производится сле­дующим образом:

Определяются значения выпрямленного тока ротора I_d1 и I_d2 соответствую­щие координатам двух заданных точек |M₁; s₁] и [М₂; S₂], через которые должна пройти механическая характеристика.

Принимается базисное напряжение схемы управления и рассчитываются коэффициенты k_u и k_i причем k_i рассчитывается для одного значения R_э соответствующего 1^oй или 2^ой точке и принимается в дальнейшем неизменным. Постоянная времени форсирующего звена в цепи ОС по току принимается равной Т_э в этой же точке.

Определяется необходимый коэффициент усиления схемы, исходя из координат заданных точек механической характеристики:

k_у = (I_d2 – I_d1) / (U_у2 – U_у1).

В свою очередь:

U_у = U_s – U­_sз = k_iI_d + k_uU_d – U_sз.

Подставив в выражение с k_у значения U_у1 и U_у2, получим:

k_у = (I_d2 – I_d1) /(k_i (I_d2 – I_d1) + k_u (U_у2 – U_у1)),

или с учетом соотношения:

U_d = E_dks – k (r₁’ s + r₂) I_d – 2 U_в,

где для первого режима работы выпрямителя:

E_dk = E_d0 – 3 x₂I_d / p;

В итоге получим:

Находится величина задающего напряжения по формуле:

.

При известном коэффициенте усиления для j^ой точки статической характеристики может быть найдено уравнение для скольжения в таком виде:

.

Задаваясь рядом значений I_dj и определяя коэффициент k и момент двигателя, можно найти соответствующие значения скольжения двигателя и по полученным данным построить искомую механическую характеристику ЭП.

Статические характеристики замкнутой и разомкнутой систем представлены на рис.2.10. Построение см. приложение 3.

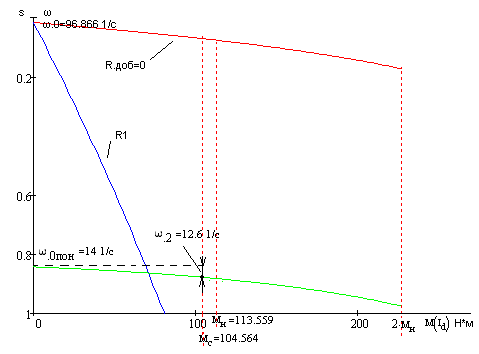
Рис.2.10 Статические характеристики замкнутой и разомкнутой систем

Выводы: В данной главе была разработана принципиальная схема силовой части электропривода и произведен выбор ее основных элементов. Были расcчитаны статические характеристики разомкнутой системы. Так как они не удовлетворяют требованиям жесткости, была разработана замкнутая система. В замкнутой системе были получены характеристики двигательного режима и режима динамического торможения с самовозбуждением. Полученные характеристики удовлетворяют заданным требованиям.

АНАЛИЗ ДИНАМИЧЕСКИХ СВОЙСТВ ЭЛЕКТРОПРИВОДА

3.1. Математическое описание электропривода

Замкнутую систему рассматриваемого ЭП с ОС по скольжению для режима стабилизации скорости при релейном, в функции выпрямленного тока, управлении коммутатором, без учёта дискретности его работы при среднем значении импульсно-регулируемого сопротивления можно представить следующей системой уравнений [3]:

Этой системе уравнений соответствует структурная схема, представленная на рис. 3.1.

На ней видно, что система содержит нелинейности и чтобы иметь возможность исследовать электропривод линейными методами, проведем линеаризацию этих уравнений относительно точки механической характеристики с координатами (М_ст; ω_ст1; S_ст1; I_ст) [3].

Рис.3.1. Структурная схема ЭП с ОС по скольжению без учёта дискретности работы коммутатора.

Линеаризованная система уравнений для точки разложения с координатами (М_ст(I_ст); ω_ст1(s_ст1)) имеет вид:

где ; ; ;

R_эо и Т_эо – эквивалентное сопротивление и электромагнитная постоянная в точке линеаризации.

При преобразовании структурной схемы линеаризованной системы можно получить передаточную функцию разомкнутой системы по управляющему воздействию:

.

Структурная схема линеаризованной системы электропривода представлена на рис.3.2.

Рис.3.2. Линеаризованная структурная схема ЭП.

Выражения для вещественной и мнимой частей соответствует амплитудно-фазовой характеристики:

; ,

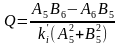где ; ; ;

.

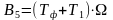Передаточная функция разомкнутой системы по возмущающему воздействию:

.

Соответствующие выражения для Р и Q:

;

.

По найденным значениям Р и Q рассчитываются амплитудно-частотная и фазо-частотная характеристики в соответствии с формулами:

;

.