
Динамические реакции
.pdfДинамические реакции в подшипниках ротора.
Описание задания. Цель расчета – приобретение опыта исследования роторных машин: вычисление масс-инерционных характеристик ротора, составление дифференциальных уравнений его вращения и уравнений для динамических реакций в подшипниках, исследование уравнений на компьютере.
Рассматриваются роторные машины типа турбины, компрессора и т. п. в неустановившемся режиме разгона или выбега.
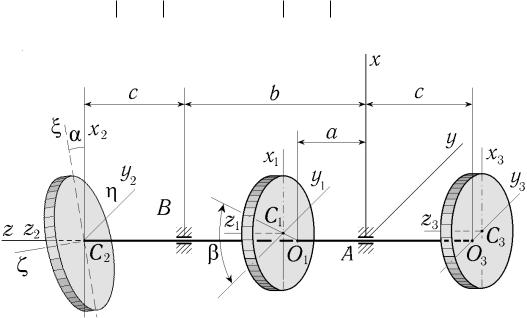
Варианты схем машин представлены на рис.1-2. Элементы конструкции считаются абсолютно жесткими, подшипники А, В – точечными, ось ротора бесконечно тонкая, совпадающая с осью вращения. Рабочие колеса принимаются однородными дисками. Через С1 , С2 , С3 на рисунках обозначены центры масс колес, через O1 , O2 , O3 – точки пересечения оси с ортогональными ей плоскостями, проходящими через центры масс колес. Колеса на оси насажены с технологическими несовершенствами: перекосом второго колеса на угол α , указанным на рисунках и смещением Oi Ci (i = 1,3) центров масс первого и третьего. Во всех вариантах для простоты принято, что центр масс второго колеса совпадает с осью вращения, а первое и третье колеса насажены без перекоса.
На рисунках введены вращающиеся с ротором ортогональные системы координат: Axyz ось, z которой совпадает с осью вращения; система коор-
динат Сi xi yi zi , |
полученная из |
Axyz , параллельным переносом в центры |
||||||||||||||||||
масс соответствующих колес; С2 ζ оси, |
которой совпадают с главными |
|||||||||||||||||||
осями инерции второго колеса. Ротор вращается под действием момента MD |
||||||||||||||||||||
и сопротивления MC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M |
Д z |
= M |
− k |
1 |
ω |
z |
; k |
1 |
= |
k |
1т |
+ 0,01N; M |
C z |
= − |
k |
2 |
ω2 ; |
|
||
|
O |
|
|
|
|
|
|
|
|
|
|
z |
|
|||||||
MO = MO Т ( 1 + 0,01n ) 100; |
|
m i |
= m i Т ( 1 + 0,01N ) ; |
|
|
|
|
|||||||||||||
O1 С1 = O1 C1Т( 1 + 0,01N ) 10-3 ; |
k 2 = |
k 2 т ( 1 + 0,01N ) 10-2 ; |
(1) |
|||||||||||||||||
a = |
a т + 0,001n; |
|
b = |
b т + 0,001N; |
c = c т + 0,001n. |
|
||||||||||||||
В расчёте требуется для конкретного ротора записать уравнения его |
||||||||||||||||||||
|
|
|
|
|
|
|
|
.. |
|
|
|
|
|
|
|
|
|
|
|
|
динамики и выразить из них , |
XB , |
YB , XA , |
YA , а затем выполнить компью- |
|||||||||||||||||
терное моделирование движения ротора.

1 |
2 |
3 |
|
|
|
4 |
5 |
6 |
|
|
|
7 |
8 |
9 |
|
|
|
10 |
11 |
12 |
|
|
|
13 |
14 |
15 |
|
|
|
Рис.1.

16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Рис.2.
Таблица 1.
Вар. |
m1т |
m2т |
R1 |
R2 |
O1 С1т |
α |
a т |
b т |
c т |
MO т |
k 1т |
k 2т |
ω0 |
|
1 |
100 |
90 |
0,23 |
0,21 |
0,2 |
0,022 |
0,20 |
0,20 |
0,15 |
12 |
1,1 |
0,3 |
0 |
5,76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
80 |
90 |
0,27 |
0,29 |
0,3 |
0,018 |
0,10 |
0,15 |
0,10 |
10 |
1,2 |
0,7 |
990 |
3,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
60 |
70 |
0,25 |
0,30 |
0,2 |
0,021 |
0,12 |
0,11 |
0,14 |
13 |
1,2 |
0,2 |
400 |
6,72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
70 |
80 |
0,12 |
0,18 |
0,1 |
0,024 |
0,15 |
0,20 |
0,15 |
8 |
1,3 |
0,8 |
590 |
1,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
80 |
90 |
0,21 |
0,28 |
0,1 |
0,028 |
0,18 |
0,18 |
0,14 |
12 |
1,6 |
0,3 |
0 |
5,52 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
40 |
60 |
0,20 |
0,18 |
0,2 |
0,015 |
0,11 |
0,12 |
0,12 |
13 |
1,1 |
0,9 |
600 |
0,96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
100 |
120 |
0,25 |
0,30 |
0,5 |
0,023 |
0,12 |
0,45 |
0,14 |
12 |
1,7 |
0,1 |
300 |
9,84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
80 |
100 |
0,21 |
0,23 |
0,2 |
0,026 |
0,12 |
0,25 |
0,12 |
6 |
1,1 |
0,9 |
500 |
2,88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
100 |
110 |
0,29 |
0,30 |
0,4 |
0,024 |
0,14 |
0,18 |
0,18 |
14 |
1,2 |
0,2 |
200 |
9,84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
70 |
90 |
0,23 |
0,28 |
0,2 |
0,016 |
0,11 |
0,22 |
0,14 |
10 |
1,3 |
0,7 |
0 |
4,80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
160 |
— |
0,31 |
|
0,3 |
0,026 |
0,30 |
0,28 |
— |
6 |
1,2 |
1,2 |
600 |
3,60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
60 |
80 |
0,24 |
0,28 |
0,2 |
0,018 |
0,10 |
0,25 |
0,10 |
15 |
1,4 |
0,1 |
400 |
5,76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
40 |
50 |
0,15 |
0,18 |
0,1 |
0,015 |
0,08 |
0,15 |
0,09 |
9 |
1,5 |
0,5 |
0 |
1,44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
80 |
90 |
0,26 |
0,30 |
0,2 |
0,022 |
0,10 |
0,10 |
0,10 |
8 |
1,3 |
0,9 |
500 |
6,24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
90 |
70 |
0,16 |
0,28 |
0,1 |
0,019 |
0,11 |
0,16 |
0,15 |
7 |
1,2 |
0,4 |
0 |
5,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
30 |
40 |
0,21 |
0,25 |
0,2 |
0,020 |
0,08 |
0,22 |
0,09 |
13 |
1,1 |
0,5 |
800 |
1,44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
70 |
80 |
0,20 |
0,28 |
0,4 |
0,026 |
0,11 |
0,30 |
0,08 |
11 |
1,3 |
0,2 |
0 |
6,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
30 |
50 |
0,18 |
0,21 |
0,3 |
0,021 |
0,10 |
0,10 |
0,09 |
9 |
1,6 |
0,5 |
0 |
2,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
60 |
70 |
0,17 |
0,19 |
0,2 |
0,023 |
0,08 |
0,25 |
0,08 |
30 |
1,5 |
0,2 |
0 |
1,92 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
50 |
70 |
0,14 |
0,17 |
0,3 |
0,024 |
0,28 |
0,08 |
0,08 |
12 |
1,7 |
0,9 |
800 |
0,72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
40 |
60 |
0,23 |
0,26 |
0,3 |
0,018 |
0,07 |
0,27 |
0,09 |
10 |
1,2 |
0,8 |
500 |
2,88 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
90 |
— |
0,31 |
— |
0,4 |
0,025 |
0,10 |
0,25 |
— |
10 |
1,6 |
1,5 |
580 |
1,68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
60 |
70 |
0,25 |
0,30 |
0,2 |
0,022 |
0,12 |
0,15 |
0,15 |
18 |
1,1 |
0,2 |
0 |
6,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
30 |
50 |
0,28 |
0,31 |
0,3 |
0,027 |
0,10 |
0,16 |
0,16 |
10 |
1,2 |
0,2 |
0 |
5,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
40 |
50 |
0,23 |
0,24 |
0,1 |
0,019 |
0,12 |
0,12 |
0,12 |
5 |
1,4 |
0,8 |
400 |
2,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
30 |
40 |
0,18 |
0,19 |
0,1 |
0,015 |
0,11 |
0,16 |
0,15 |
26 |
1,3 |
0,1 |
600 |
1,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
40 |
30 |
0,20 |
0,17 |
0,1 |
0,018 |
0,08 |
0,25 |
0,07 |
19 |
1,5 |
1,6 |
600 |
0,48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
50 |
50 |
0,22 |
0,22 |
0,3 |
0,024 |
0,12 |
0,10 |
0,12 |
5 |
1,2 |
1,3 |
490 |
1,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
50 |
40 |
0,18 |
0,15 |
0,2 |
0,017 |
0,11 |
0,12 |
0,12 |
6 |
1,3 |
0,8 |
500 |
0,96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
100 |
|
0,35 |
— |
0,3 |
0,023 |
0,18 |
0,18 |
— |
3 |
1,1 |
1,6 |
400 |
3,36 |
Исходные данные, для каждого варианта определяются по формулам (1) и табл. 1:
Будем представлять реакции в подшипниках в виде суммы статических и добавочных динамических реакций, причём ограничимся нахождением только последних.
Тогда при указанном выборе системы координат получаем следующее уравнение вращения ротора:
.. |
---- |
|
Jzz |
= MA z ( F k ) , |
(2) |
k
которое дополним уравнениями для нахождения добавочных динамических реакций, имеющими такой вид:
|
|
|
.. |
|
m x |
|
. |
|
X + X , |
|
|
||||||
|
− m y |
− |
2 |
= |
|
|
|||||||||||
|
m x |
C .. |
|
|
C . |
|
|
A |
|
|
B |
|
|
|
|||
|
C |
|
− |
m y 2 |
= |
Y + Y , |
|
|
|
||||||||
|
|
|
|
|
C |
|
|
|
A |
|
|
B |
|
|
|
|
|
|
.. |
|
|
. |
|
|
z |
|
Y |
|
z |
Y |
(3) |
||||
|
− J |
+ |
J 2 |
= − |
|
− |
, |
||||||||||
|
xz .. |
|
yz . |
|
z |
|
A |
|
A |
z |
|
B |
B |
|
|||
|
− J |
− |
J 2 |
= |
X |
|
+ |
X . |
|
||||||||
|
yz |
|
|
|
xz |
|
|
|
A |
A |
|
|
B |
|
B |
|
|
Здесь: – угол поворота ротора; |
m – его масса; |
xC и yC – коорди- |
|||||||||||||||
наты его центра масс в осях Oxyz ; |
Jxz , Jyz , |
Jzz |
– |
моменты инерции рото- |
|||||||||||||
---- |
---- |
… – |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ра в этих осях; F1 |
, F2 , |
действующие на ротор внешние активные си- |
|||||||||||||||
лы; zA , zB – координаты точек A и B ; |
XA , |
YA , |
XB , YB |
– компоненты до- |
|||||||||||||
|
|
|
|
|
---- |
---- |
|
|
|
|
|
|
|
|
|
|
|
бавочных динамических реакций R A , R B в подшипниках. |
|||||||||||||||||
Напомним, что моменты инерции твёрдого тела совпадают – |
с точностью до |
||||||
знака – с компонентами оператора инерции (тензора инерции) данного тела. |
|||||||
- |
– оператор инерции тела относительно полюса O, то |
||||||
Именно, если JO |
|||||||
матрица данного оператора в системе координат Oxyz имеет вид |
|||||||
|
|
|
Jxx |
− Jxy |
− Jxz |
|
|
I |
O xyz |
|
|
Jyy |
− Jyz |
|
|
|
= |
− Jyx |
. |
(4) |
|||
|
|
|
− Jzx |
− Jzy |
Jzz |
|
|
Здесь в виде верхнего индекса указана используемая система координат. В выкладках, которые сопровождают выполнение данного типового расчёта, приходится иметь дело с матрицами и столбцами, состоящими из компонент операторов и векторов в различных системах координат. Во избежание путаницы целесообразно все используемые системы координат указывать явно.
Применительно к типовому расчёту ДР уравнения (2), (3) можно несколько конкретизировать. Именно, примем за начало координат точку A; тогда слагаемые с zA исчезнут. Далее, учтём, что в сумму, стоящую в пра-
вой части (2), входят – по условию – |
лишь два слагаемых: проекции MD z и |
|
MC z |
------ |
------ |
вращающего момента MD и момента сопротивления MC на ось z . То- |
||
гда, |
принимая во внимание (1) явные выражения для MD z и MC z , предста- |
|
|
. |
. |
вим эту сумму в виде M0 − k1 − k2 2 .
При решении задач по теме “Динамика твёрдого тела, вращающегося вокруг неподвижной оси” на этапе составления уравнений движения тела можно придерживаться следующей последовательности действий:
1°. Найти массу и радиус-вектор центра масс твёрдого тела (определив тем самым коэффициенты m, xC и yC ).
2°. Найти матрицу оператора инерции твёрдого тела в используемой систе-
ме координат (определив тем самым коэффициенты Jxz , Jyz , |
Jzz ). |
|
|
|
||||||||
3°. Записать уравнения динамики твёрдого тела. |
|
|
|
|
|
|||||||
Поскольку масса, радиус-вектор центра масс и оператор инерции абсо- |
||||||||||||
лютно твёрдого тела – |
аддитивные величины, то в задании расчёта Д-6 эти |
|||||||||||
характеристики ротора вычисляются суммированием: |
|
|
|
|
|
|||||||
m = mj , |
--- |
|
1 |
--- |
|
I |
Axyz |
|
Ij |
Axyz |
|
|
rC |
= |
−− |
mj rC |
, |
|
= |
|
, |
(5) |
|||
j |
|
|
m |
j |
j |
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
||||
где j – номер диска, |
Cj |
– |
его центр масс |
|
(вместо самих операторов |
|||||||
инерции |
|
|
|
|
|
|
|
|
|
|
|
|
в этих формулах фигурируют их матрицы).
Таким образом, все указанные характеристики следует сперва рассчитать по отдельности для каждого диска. Рассмотрим, как это делается.
|
|
yP2 + zP2 |
|
− xP yP |
||||
IPOxyz = |
m |
− yP xP |
|
|
zP2 + xP2 |
|||
|
|
|
|
|
|
|
− zP yP |
|
|
|
− zP xP |
|
|||||
O ζ |
m R |
2 |
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|||
Ij |
= −−−− |
0 |
1 |
0 |
|
|||
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
0 0 |
|
|||
−xP zP
−yP zP , xP2 + yP2
(6)
Формулы (6) представляют в явном виде соответственно матрицу оператора инерции материальной точки P массы m в произвольной системе координат Oxyz и матрицу оператора инерции однородного тонкого диска массы m и радиуса R в системе его главных центральных осей инерции O ζ . При этом предполагается, что ось ζ перпендикулярна плоскости диска, а через j вновь обозначен номер диска.
Начав с выражения, даваемого второй из формул (6), можно вычислить матрицу оператора инерции диска в любой системе координат, пользуясь следующими преобразованиями:
I. Переход от центральных осей к осям, им параллельным:
IjOxyz |
= IjO ζ + ICO xyz . |
(7) |
II. Переход к новым осям с тем же началом:
IjOxyz |
= IjO ζ т . |
(8) |
В формулах (7), (8): ζ и xyz – соответственно “старые” и “новые” координатные оси; C – центр масс тела j ; т – символ транспонирования матрицы. Последнее слагаемое в (11) обозначает матрицу оператора инерции воображаемой материальной точки, у которой масса равна массе тела j и которая помещена в его центр масс; элементы этой матрицы вычисляются в соответствии с первой из формул (6). Через обозначена матрица направляющих косинусов между “старыми” и “новыми” осями:
γx= γyγz
γx |
γxζ |
γy |
γyζ |
γz |
γz ζ |
, γx = cos (x, η ) , . . .
Что касается вычисления радиус-векторов центров масс, то столбец компонент радиус-вектора произвольной точки P преобразуется при перехо-
де от “старых” осей ζ |
к “новым” осям xyz по следующим формулам: |
|
||||||||
r Oxyz |
= |
r O 'xyz |
+ |
r Oxyz |
, |
r Oxyz |
= |
r O ζ |
; |
(9) |
P |
|
P |
|
O ' |
|
P |
|
P |
|
|
здесь первая формула соответствует параллельному переносу осей из точки O' в точку O , а вторая – повороту осей при том же начале.
После того, как – в соответствии с последней из формул (9) – матрица оператора инерции ротора будет вычислена, Вы сможете, учитывая (8), найти моменты инерции Jxz , Jy z , Jzz .
Помните, что центробежные моменты инерции входят в матрицу I O xy z со знаком “минус”, и не забудьте изменить знак!
Получив уравнения динамики ротора в форме (2), (3), введём обозначе-
. ..
ния ωz = , εz = и найдём из полученной системы нужные нам расчётные формулы для εz , XB , YB , XA , YA (их следует записать именно в этом
порядке; в формулах могут фигурировать величины, уже определённые ра-
.
нее). Заметим, что дифференциальное уравнение = ωz можно не рассма-
тривать (расчётные формулы не зависят от ), так что система дифферен-
.
циальных уравнений (1) сводится к одному уравнению ωz = εz (ωz ). При этом XB , YB , XA , YA играют роль вспомогательных переменных.
Теперь всё готово для работы с программой dr. В меню для ввода параметров задания присутствуют две группы параметров: в первую входят m1,
m2 , R1 , R2 , δ, α, |
a, b, c, M0 , k1 , k2 , а во вторую – |
ωz(0)и τ. |
Буквой |
|
δ обозначено расстояние O1 C1 . |
Параметры второй группы должны быть за- |
|||
даны обязательно. |
Поскольку |
коэффициенты xC , yC , |
zB , Jxz , |
Jyz , Jzz |
обычно находят численно, то значения большей части параметров первой группы, как правило, вводить не нужно. Что касается ввода расчётных формул, то в их правых частях могут фигурировать – помимо параметров первой группы – переменная состояния ωz и величины, определённые предыдущими формулами.
|
|
|
По завершении интегрирования уравнений движения программа dr |
|||||||
позволяет вывести на экран графики зависимостей величин ωz , εz , RA |
|
---- |
|
, |
||||||
|
|
|||||||||
|
R A |
|
||||||||
RB |
|
|
---- |
|
от t, а также таблицу значений ωz , εz , XA , YA , |
XB , YB , RA , RB |
||||
|
|
|||||||||
|
|
R B |
|
|||||||
в отдельные моменты времени. |
|
|
|
|
|
|||||
|
Пример выполнения задания: Вар. 31 ( n = 3, |
N = 7 ). |
||||||||
Рассматривается переходный режим вращения ротора турбины после увеличения нагрузки. Значение вращающего момента M Д z = MO − k 1 ωz , Момент сил сопротивления, пропорциональный квадрату угловой скорости вращения вала M C z
Дано: MO = 1950 H• м, k 1 = k 1т + 0,01N = 1.57 H• м• c, k 2 = 0.039 H• м• c2 .
Массы дисков m1 = 47 кг; m2 = 57 кг; m3 = 37 кг. Их радиусы R1 = 0.17 м,
R2 = 0.2 м, R3 = 0.15 м. Эксцентриситеты первого и третьего диска соответственно равны: O1 C1 = 0.0004 м и O3 C3 = 0.0003 м.
Рис.3.
Углы α = 0.019 рад, β = 0.68 рад. Расстояния между дисками а = 0.133 м; b = 0.267 м; c = 0.093 м. Начальная угловая скорость вращения ротора ωz (0) = 600 рад/с. Время выхода на установившийся режим = 0.48 с.
Требуется:
1.Определить в осях Аxyz координаты центра масс C ротора и его оператор инерции;
2.Составить уравнения вращательного движения ротора и уравнения для определения динамических реакций в подшипниках;
3.Проинтегрировать дифференциальные уравнения движения на заданном интервале времени и определить изменение во времени ди-
намических реакций.
4.Построить графики ωz ( t ), ε z ( t ), RА ( t ), RВ ( t ).
Вычисление масс-инерционных характеристик ротора
Масса ротора определяется как сумма масс колес:
m = m1 + m2 + m3 = 47 + 57 + 37 = 141 ( кг ).
Координаты центров масс дисков Ci в системе координат Аxyz в соответствии с рис. 3.
C1 |
{0.000252 , − 0.000312, |
0.133} ; |
|
|
|
|
|
|
|||||||
C2 |
{0 , 0, 0.36} ; |
|
|
|
|
|
|
|
|
|
|
||||
C3 |
{0 , |
0.0003, − 0.093} |
|
|
|
|
|
|
|
|
|
|
|||
Координаты центра масс ротора xС , уС находятся по формулам |
|||||||||||||||
|
1 |
4 |
|
= 0.837• 10 – 4 |
|
|
|
|
1 |
|
|
4 |
= − 0.255• 10 – 4 м. |
||
xС = |
|
|
mi xC |
м; yС |
= |
|
mi yC |
||||||||
|
|
|
|
|
|||||||||||
|
m i = 1 |
|
i |
|
|
|
|
|
m i = 1 |
i |
|||||
|
|
|
|
|
|
|
|
|
|||||||
Тензор инерции второго диска в осях C2 η ζ имеет вид |
|
||||||||||||||
|
|
|
|
|
C2 ζ |
|
mR |
2 |
1 |
0 |
0 |
|
|||
|
|
|
|
|
= |
|
|
1 |
0 |
|
|
||||
|
|
|
|
|
I2 |
4 |
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
2 |
|
||||
Тензоры инерции первого и третьего дисков имеют аналогичный вид
|
2 |
1 0 0 |
|
|
2 |
1 0 0 |
||||
I1C1 x1 y1 z1 = |
mR1 |
|
0 1 0 |
|
; |
I3C3 x3 y3 z3 = |
mR3 |
|
0 1 0 |
|
4 |
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
0 0 2 |
|
|
|
|
|
0 0 2 |
|
В осях C2 x2 y2 z2 тензор инерции второго диска определяется с помощью матричного преобразования
I2C2 x2 y2 z2 = I2C2 ζ т
В этом случае матрица такова:
|
cosα |
0 −sinα |
|
|
= |
0 |
1 0 |
|
|
sin α 0 cosα |
|
Так как угол перекоса второго диска α на самом деле мал, то далее будем пренебрегать величинами второго и более высокого порядка малости по
α, пологая sin α = α и cos α = 1. В таком случае
C x y |
z |
2 |
|
m R 2 |
1 |
0 − α |
1 |
0 0 |
|
1 0 |
α |
|
|
I2 2 2 2 |
|
= |
2 2 |
|
0 |
1 0 0 |
1 0 |
0 1 |
0 = |
||||
|
|
|
|
||||||||||
|
|
|
|
4 |
|
α |
0 1 |
0 |
0 2 |
− α 0 |
1 |
|
|
