2.5 Еластичність.

Коефіцієнт еластичності широко використовується в дослідженнях споживацького попиту на товари залежно від цін на ці товари або доходів споживачів Високий коефіцієнт еластичності означає слабкий ступінь задоволення потреби; низький указує на велику настійність даної потреби.

5. Характеристику відносної зміни результату виробництва на одиницю відносної зміни витрат -го ресурсу дає показник еластичності випуску по витратах -го ресурсу:

2.5.1

Потреба в -у ресурсі як функція величини випуску і об'ємів інших ресурсів визначається виразом

На основі аналізу коефіцієнтів еластичності у виробничій функції Кобба-Дугласа можна виділити:

а) пропорційно зростаючу виробничу функцію;

б) непропорційно зростаючу;

в) убуваючу.

6. Для будь-якої пари ресурсів і можна визначити граничну норму заміщення -го ресурсу -м ресурсом. Ця норма рівна:

2.5.2

7. Відносним показником заміщення ресурсів є еластичність заміщення:

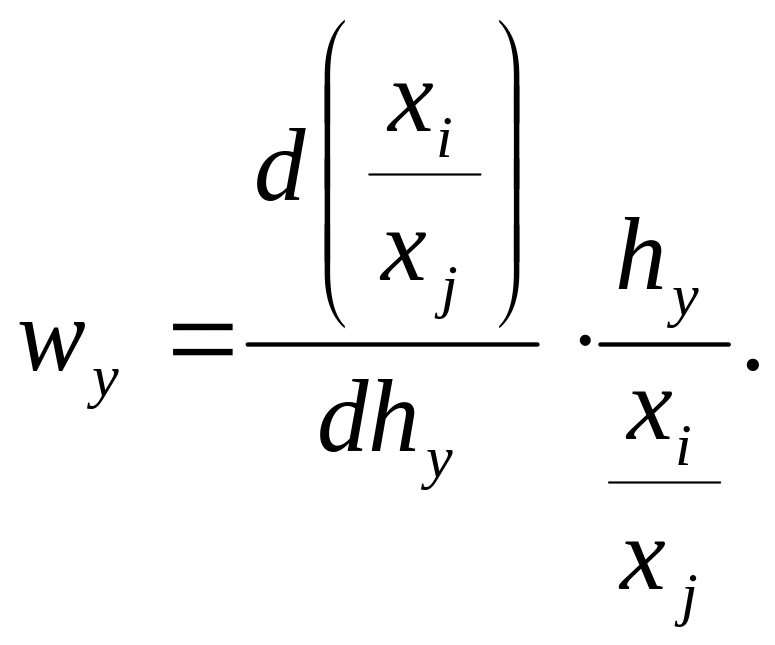2.5.3

Відповідно до виду виробничої функції еластичність заміщення може бути змінною (залежної від об'ємів ресурсів) або постійною величиною. Теоретичний і практичний інтерес представляють виробничі функції з постійною (відмінної от1) еластичністю заміщення праці виробничими фундаціями і з постійною (змінною) віддачею на одиницю масштабу виробництва.

Теоретичний і практичний інтерес представляють виробничі функції з постійною (відмінної від 1) еластичністю заміщення праці виробничими фундаціями і з постійною (змінною) віддачею на одиницю масштабу виробництва.

Прикладом такого роду функцій є функція CES:

,

для якої еластичність заміщення .

, С0 і С1 – постійні.

2.6 Приклад.

Розрахунок параметрів виробничої функції розглянемо на наступному прикладі.

Є дані про виробництво продукції і витрати ресурсів за десять років:

Випуск продукції	4,2	5,1	6,2	7,3	8,4	9,5	10,5	11,4	12,1	12,9
Витрати праці	1,7	1,9	2,2	2,5	2,9	3,2	3,5	3,7	4	5,2
Витрати фондів	4,7	5,6	6,6	7,7	8,9	9,8	11,2	12,7	132,8	15

Побудувати виробничу функцію, розрахувати її параметри, порівняти отримані результати з фактичними даними.

Аналіз необхідно починати з визначення аргументів виробничої функції, враховуючи, що це повинні бути найістотніші чинники виробництва

Стосовно даного прикладу такими є витрати праці і витрати основних фундацій.

Враховуючи єство виробничої функції, як її змінні прийняті:

- витрати праці. Ця змінна в найбільшій мірі відображає об'єм використаних на підприємстві засобів праці.

- витрати основних фундацій. Вибір такої змінної обумовлений тим, що основні виробничі фундації тісно були пов'язані з випуском продукції.

І як залежна змінна був прийнятий річний випуск продукції

Поширеною виробничою функцією є функція Кобба-Дугласа:

Тут позначає величину випуску продукції; - витрати праці; - об'єм виробничих фундацій; - параметри.

Побудову конкретної моделі проведемо, використовуючи метод якнайменших квадратів.

Для цього приведемо функцію до лінійного вигляду:

де . Застосувавши метод якнайменших квадратів, отримаємо систему рівнянь:

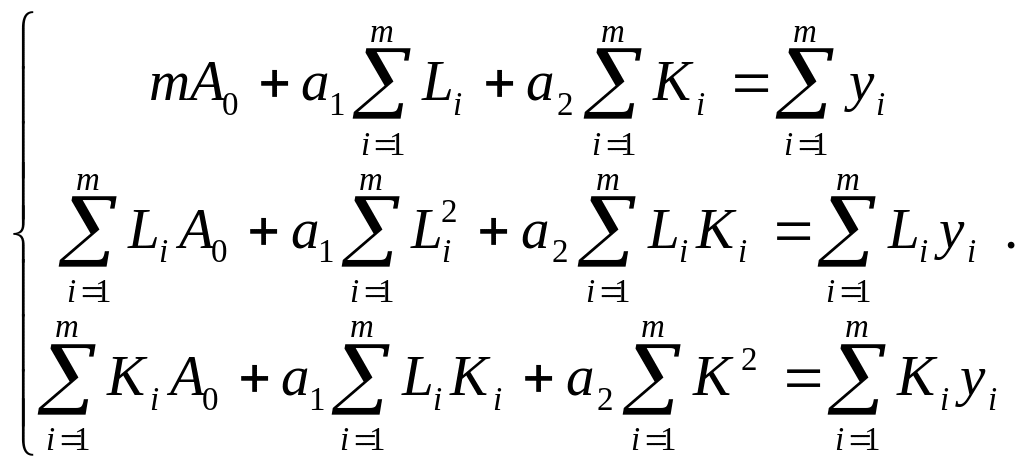
Розрахунки були приведені в таблиці:

1	1.4351	0,5306	1,5476	0,2816	2,3950	0,6211	0,7615	2,2210
2	1.6292	0,6419	1,7228	0,4120	2,9679	1,1058	1,1058	2,8068
3	1.8245	0,7885	1,8871	0,6217	3,5610	1,4880	1,4880	3,4430
4	1.9879	0,9163	2,0412	0,8396	4,1666	1,8704	1,8704	4,0577
5	2.1282	1,0647	2,1861	1,1336	4.7788	2,3275	2,2666	4,6525
6	2.2513	1,1632	2,2824	1,3529	5,2093	2,6549	2,6187	5,1314
7	2.3514	1,2528	2,4159	1,5694	5,8366	3,0267	2,9458	5,6804
8	2.4336	1,3083	2,5416	1,7117	6,4598	2,5416	3,1839	6,1852
9	2.4932	1,3863	2,6247	1,9218	6,8889	3,6386	3,4563	6,5439
10	2.5572	1,6487	2,7080	2,7281	7,3335	4,4648	4,2161	6,9249
?	21.0916	10,7013	21,9574	12,5724	49,5974	23,7394	23,7548	47,6538

Система рівнянь має вигляд:

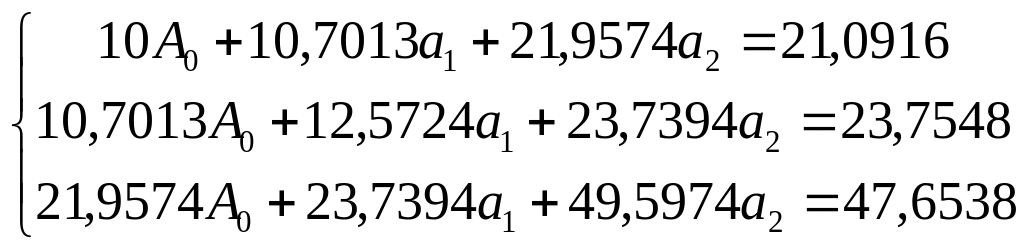
Вирішивши систему, одержуємо:

Функція має вигляд:

З метою оцінки вибраної форми зв'язку і точності апроксимації був визначений коефіцієнт множинної кореляції

=

і критерій Фішера

=

По таблиці критичних крапок Фішера (додаток 1) знаходимо критичне значення статистики

де - - число спостережень;

- число чинників (змінних);

- рівень значущості, рівний 0,05.

Оскільки , те рівняння значущо.

На підставі отриманих оцінок, можна зробити висновок про те, що форма зв'язку була вибрана правильно і знайдена виробнича функція об'єктивно відображає існуючу закономірність зв'язку між даними показниками.

Розрахуємо основні характеристики виробничої функції. що відображають ефективність використовування основних видів ресурсів в умовах підприємства.

В результаті отримаємо наступні рівняння для розрахунку.

1. Середня продуктивність праці

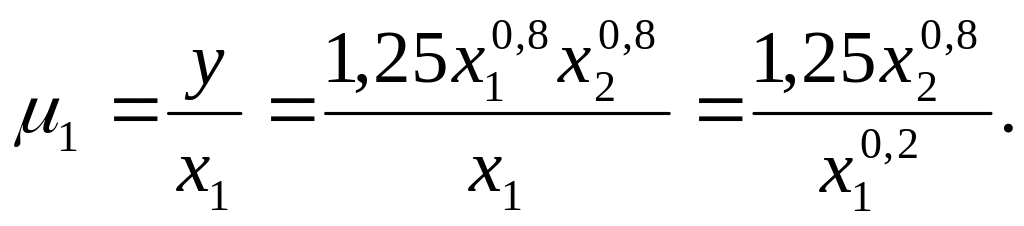
Із збільшенням витрат праці середня продуктивність праці знижується. Це було викликано тим, що об'єм виробничих фундацій, залишається незмінним. Збільшення ж виробничих фундацій веде до зростання продуктивності праці.

2. Середня фондовіддача

Із збільшенням фундацій середня фондовіддача зменшується. Збільшення ресурсів праці (при незмінних фундаціях) веде до зростання фондовіддачі.

Вирази (1) – (2) характеризують середню продуктивність праці і середню фондовіддачу, то0есть показують відповідно середня кількість продукції, проведена одним робітникам, і середня кількість продукції, що доводиться на одиницю використаних основних фундацій.

Диференціюючи функцію ( ) по різних чинниках, визначимо абсолютну зміну випуску продукції, викликану зміною даних чинників по кожному року аналізованого періоду:

,

де - - повні й диференціал функції ( ), приріст випуску продукції в рік ;

- приріст або зменшення основних фундацій і витрат праці відповідно.

Приватні похідні і показують граничну продуктивність ресурсів, тобто ефективність додаткових витрат за інших рівних умов

3. Гранична продуктивність праці

показує граничний приріст випуску товарної продукції при збільшенні трудових ресурсів на одиницю і при незмінних основних фундаціях.

Із збільшенням витрат праці при незмінних фундаціях гранична продуктивність праці знижується. Із збільшенням об'єму фундацій при незмінних трудових ресурсах (тобто із зростанням фондовооружонності праці) гранична продуктивність праці зростає. Одночасна зміна обох змінних може привести до різних результатів.

4. Гранична фондовіддача

показує, скільки додаткових одиниць продук5ции забезпечує приріст на одну одиницю основних фундацій при незмінній кількості інших ресурсів.

Із збільшенням об’єму виробничих фундацій при незмінних трудових ресурсах гранична фондовіддача знижується. Із збільшенням об’єму трудових ресурсів при незмінних фундаціях гранична фондовіддача зростає.

Для характеристики впливу кожного ресурсу на зростання виробництва окрім показників середньої і граничної ефективності необхідно визначити еластичність випуску від витрат різних ресурсів.

Коефіцієнт еластичності показує відношення відносного приросту виробництва до відносного приросту витрат -го ресурсу.

5. Еластичність випуску продукції по витратах праці

Даний показник означає, що при збільшенні витрат праці на 1% випуск продукції збільшиться на 0,8%.

6. Еластичність випуску продукції по витратах праці

Значення показника аналогічне попередньому.

Таким чином, показники еластичності ук5азывают на характер зміни функції при зміні аргументу.

По сумі коефіцієнтів еластичності можна прослідити тенденцію зміни випуску продукції при одночасній зміні всіх чинників на 1%. При цьому величина говорить про позитивний ефект розширення масштабів виробництва, в осоружному випадку говорять про убуваючу ефективність виробництва, а рівність суми одиниці розглядається як рівновага темпів зміни випуску продукції і зміна ресурсів.

Таким чином, аналіз ефективності виробництва на підставі виробничої функції дозволяє визначити внесок кожного з чинників виробництва Вт збільшення випуску продукції.

Виробнича функція дозволяє розрахувати потребу в одному з ресурсів при заданих об’ємі і величині іншого ресурсу. Потреба в ресурсах праці рівна:

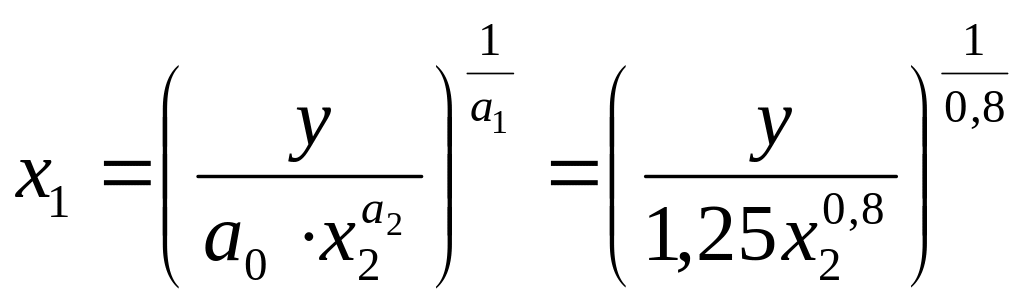
Потреба у виробничих фундаціях складає:

Виробнича функція дозволяє досліджувати питання співвідношення, заміщення, взаємодії ресурсів. Зокрема, в даному випадку на основі двох останніх співвідношень визначається важливий економічний показник – фондовооруженность праці:

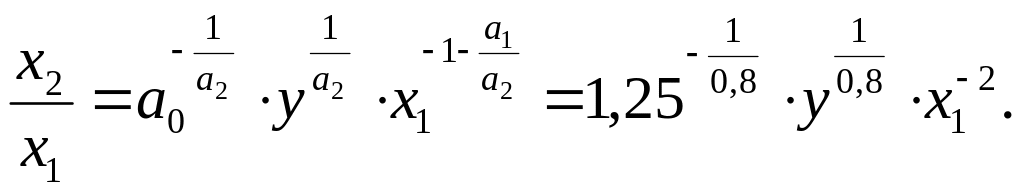
Дослідження розвитку виробництва по формулі ( ) дозволяє зіставляти ресурси, що використовуються, по коефіцієнтах еластичності за допомогою норм взаємозамінності

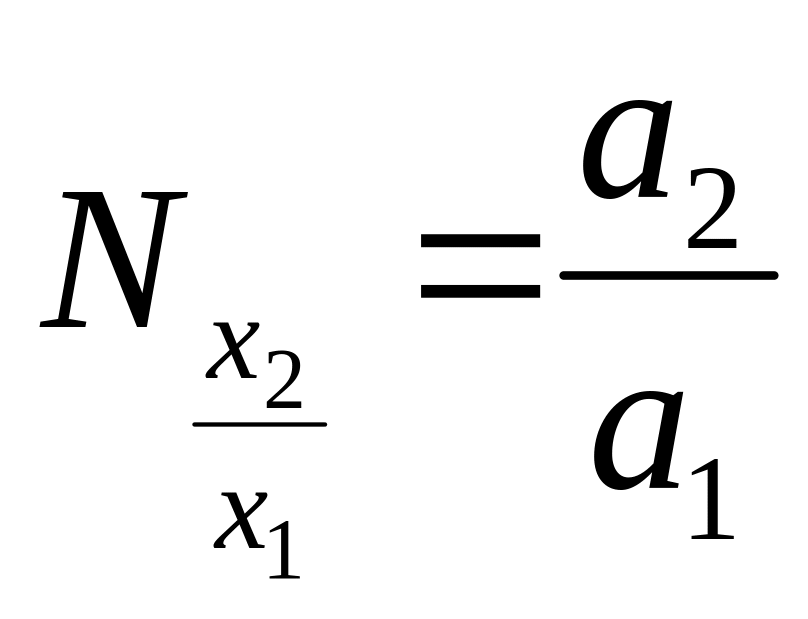- усереднена норма замінюваності одиниці основних фундацій працею.

Ця формула показує, яку частину одиниці праці можуть замінювати одиниці основних фундацій, тобто одна гривна основних фундацій замінює одиниць праці.

Взаємодіючі в рамках виробничої функції ресурси можуть заміщати один одного. Гранична норма заміщення витрат праці виробничими фундаціями в даній задачі рівна:

Гранична норма заміщення, як видно з отриманого співвідношення залежить не тільки від параметрів функції (коефіцієнтів і ), але і від співвідношення об’ємів ресурсів. Знак мінус означає, що при фіксованому об’ємі виробництва збільшення одного ресурсу відповідає зменшення іншого, і навпаки.

Вплив співвідношення об’ємів ресурсів на граничну норму заміщення знаходить свій вираз в показнику еластичності заміщення ресурсів, який визначається як відношення відносних приростів фондовооруженності праці і граничної норми заміщення ресурсів:

де

Еластичність заміщення ресурсів для даної функції рівна одиниці, тобто зміна фондовооруженності праці на 1% відповідає зміна граничної норми заміщення також на 1%.