2. Виробнича функція Кобба – Дугласа.

2.1 Виробнича функція Кобба – Дугласа зв'язує випуск з величиною виробничих фундацій (об'єм основного капіталу) і витратами живої праці (витрати праці) :

, де і - постійні.

Функція Кобба – Дугласа задовольняє всім перерахованим умовам, якщо .

В даному випадку вибір статечної функції був обгрунтований двома причинами: по-перше, статечна функція, за допомогою логарифмування, приводиться до лінійної, по-друге, вона враховує нульовий ефект виробництва, тобто, при якому-небудь нульовій чиннику виробнича функція звертається в нуль. З економічної точки зору це означає, що не можна отримати продукцію не використавши одного з видів ресурсів.

Побудова виробничої функції була пов'язана з обробкою великих об'ємів економічної інформації. Для побудови виробничої функції формується статистична сукупність спостережень, яку можна записати у вигляді матриці, де - кількість одиниць сукупності спостережень; - кількість показників по кожній сукупності.

Ця сукупність спостережень повинна бути обов'язково однорідною. Функція Кобба – Дугласа однорідна із ступенем однорідності . Це означає, що при зростанні витрат кожного з чинників в раз випуск зростає в раз.

Якщо , то функція має зростаючу віддачу від масштабу.

Якщо, то функція має убуваючу віддачу від масштабу.

Якщо , то функція має постійну віддачу від масштабу

З економічної точки зору однорідність можна забезпечити, якщо досліджувати: однотипні підприємства, які мають приблизно однакові умови виробничого процесу, а показники в розрізі підприємств були розраховані по одній і тій же методиці, за один і той же період, мають однакові одиниці вимірювання.

Аналітична форма виробничої функції залежить від характеру взаємозв'язків чинників з результативною ознакою, а так само між собою. Для окремого підприємства виробнича функція може зв'язувати об'єм випуску продукції ( в натуральному або вартісному виразі) з витратами робочого часу ( різні види трудової діяльності), різними видами використаної сировини, основного капіталу, енергії. Виробничі функції такого типу відображають технологію виробництва. Щоб встановити аналітичний вид залежності для кожного конкретного випадку, необхідно зібрати статистичні дані. Сукупність складає вибірку. Практично можна вважати, що число початкових даних повинне бути в 3-5 разів більш ніж число шуканих величин. Математичний апарат був розроблений для лінійного виду залежності. Проте це не поменшує спільності, оскільки будь-яку іншу форму залежності можна звести до лінійної.

Отже

де - помилка обчислень, але вона містить і дію неврахованих чинників.

2.2 Параметри виробничої функції

Позначимо вектор невідомих параметрів, вектор залежної змінної, матрицю незалежних змінних, вектор помилок . Тоді лінійну модель в матричному вигляді: .

Для визначення невідомих параметрів використовується МНК. Після відповідних перетворень, отримаємо

де

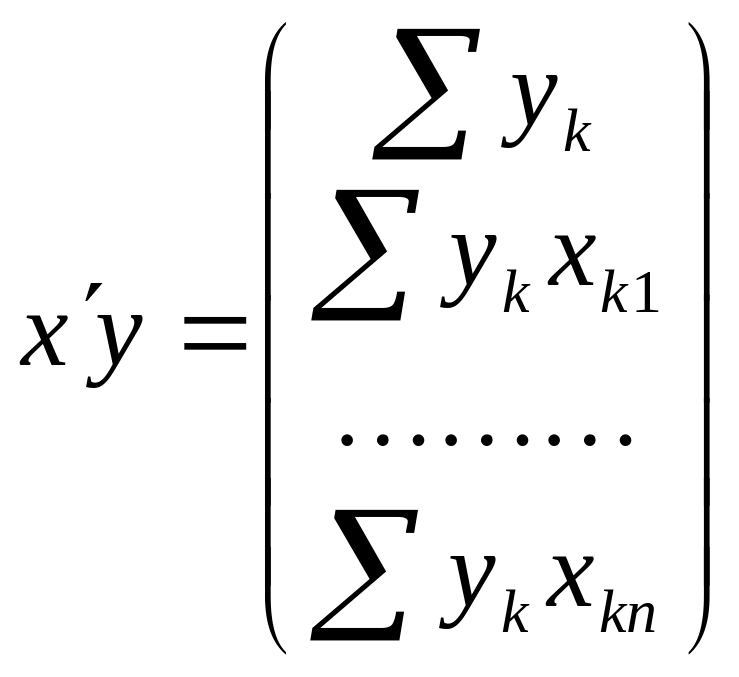2.2.1

Побудову виробничої функції можна здійснювати на основі використовування покрокової лінійної регресії. Розглянемо її суть.

Алгоритм покрокової регресії припускає на першому етапі розрахунок матриці коефіцієнтів парної кореляції, яка характеризує тісноту взаємозв'язку показників між собою і з результативною ознакою.

, . 2.2.2

Якщо зв'язок між чинниками тісний, то можна говорити про наявність мультіколінеарності, яка негативно впливає на оцінку параметрів виробничої функції, оскільки математичний апарат теорії кореляції і регресії був розроблений виходячи з допущення відсутності зв'язку між чинниками

Проаналізувавши тісноту зв'язку між чинниками, виключаємо з виробничої функції один з двох чинників, зв'язок між якими достатньо тісний.

Відповідно до алгоритму покрокової регресії на першому етапі побудови виробничої функції в модель вводиться той показник, який має найбільший зв'язок з результативною ознакою і т. д., тобто на кожному кроці в модель додатково вводиться нова змінна, що має найтісніший зв'язок з результативною ознакою серед решти змінних.

Слід звернути увагу на кількісну опеньку параметрів aj. Введення кожної нової змінної впливає на попереднє значення параметра, і цей вплив буде тим більше, чим тісніше взаємодіють між собою змінні.

Властивості виробничих функцій.

Розглянемо виробничу функцію багаточинника, що двічі диференціюється . Вона володіє наступними властивостями.

1. Функція позитивна в області визначення.

2. Функція має позитивні приватні похідні - які називаються граничною продукцією.

3. Приватні похідні другого порядку, задовольняючі умовам характеризують закон убуваючої ефективності виробництва.