Stabiilsuse kriteeriumid.

Nendega saab kergendada stabiilsuse määramist. Nad kõik baseeruvad diferentsiaal võrrandil ja neid on mitu.

1. Routh. See on algebraline kriteerium ja stabiilsuse määramiseks kasutatakse diferentsiaal võrrandis olevaid koefitsiente.

paaris	a4	a2	a0	0
paaritu	a3	a1	0	0
				0
			0	0
			0	0
		0	0	0

Süsteem on stabiilne kui esimese veeru koefitsiendid on kõik positiivsed ja ei võrdu nulliga.

2. N ygwist'i kriteerium – sel juhul stabiilsuse määramiseks kasutatakse lahtise süsteemi sageduskarakteristikuid.

Igas süsteemis on olemas tagasiside ja ta peab olema negatiivne, siis süsteem on stabiilne. Tagasiside seade pöörab X_V faasi 180º võrra negatiivse tagasiside teostamiseks. Kui süsteemi osa mis arvutatakse tagasisidega on ideaalne. Kui tagasiside on ideaalne, siis ta ei kutsu esile faasinihkeid. Seega ideaalne:

XS	Θ=0º
XV	Θ=0º
XTS	Θ=180º

Reaalse süsteemi elemendid viivad sisse faasinihkeid ja tavaliselt need on negatiivsed ja suurenevad sageduse suurenemisel. Võib tekkida olukord, et mingisugusel sagedusel süsteemi väljundis tekib nihe –180º. Reaalne:

XS	Θ=0º
XV	Θ=-180º
XTS	Θ=180º

Süsteemi sulgemisel X_S ja X_ts vahel faasi nihe on 0º ja süsteemis tekib "+ts". Ja süsteem võib minna tasakaalust välja. Aga selleks on vaja lisatingimust, et sellel sagedusel süsteemi üldülekande tegur oleks suurem kui 1.

Ebastabiilsuse tingimusteks on seega Θ=Θ_V-Θ_S=-180º ja |W|=>1.

Kui üks nendest tingimustest ei ole täidetud on süsteem stabiilne. Lähtudes nendest tingimustest saab süsteemi stabiilsuse määrata lahtise süsteemi sageduskarakteristiku järgi.

Kui tahame AFSK järgi stabiilsust.

 = 30 …. 40 %

A = 30 --- 40 %

Logaritmilise karakteristiku järgi.

S üsteem on stabiilne kui lahtisi süsteemi AFSK ei haara punkti koordinaatidega (-1;0).

Mihhailovi stabiilsus.

Mihhailovi stabiilsuse määramiseks tuleb kasutada suletud süsteemi ülekande funktsiooni võtame nimetaja

selle võrrandi lahendid on p_n; p_n-1; ...; p; selle võrrandi võib kujutada ka nii asendades siin p=jω saame p_n...p₁ – operaatorvõrrandi lahendid.

Süsteemi stabiilsuseks on vaja, et kõik α-d oleksid negatiivsed. Kuna on vektor siis on ka on ka vektor. Vaatame kuidas käitub vektor ja

pöörab +π võrra.

Muudame ω = -∞ kuni +∞ ja selle tagajärjel vektor pöörab -π võrra ja vektor

Kui muudame ω = 0 kuni +∞ siis pöörab –0,5π ja pöörab +0,5π võrra. Kuna selliste vektorite arv on võrdne n –iga ja süsteemi stabiilsuseks on vaja, et igal vektoril oleks –α, siis süsteem on stabiilne kui üldine pöördenurk on võrdne +n*0,5π.

M – Mihhailovi vektorimoodul; Θ – Mihhailovi vektoripöördenurk.

Mihhailovi kriteeriumi järgi süsteem on stabiilne, kui Mihhailovi vektor liigub vastupäeva ja läbib n kvadranti, kus n on diferentsiaal võrrandi järk ja stabiilsuse uurimiseks on vaja võtta suletud süsteemi ülekande funktsioon ja selle funktsiooni nimetaja järgi määrata Mihhailovi vektor.

Automaatreguleerimissüsteemide kvaliteet.

ARS kvaliteet mõõdetakse vigade suurusega, mis tekivad reg. protsessi käigus. Kvaliteeti võib iseloomustada eraldi olevate näitajate abil või integraal kriteeriumite abil, mis võimaldavad võrrelda omavahel süsteeme kvaliteedi järgi, võib olla kahte tüüpi.

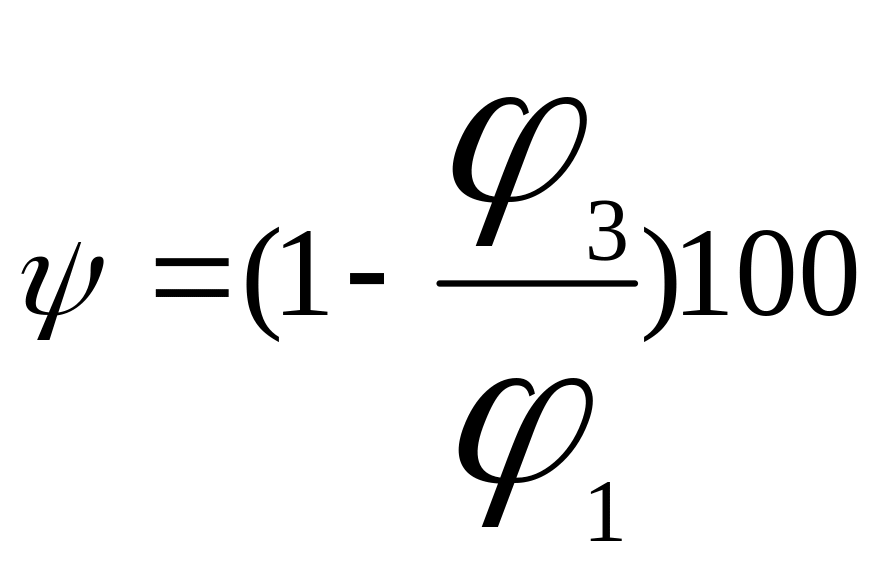
-max kõrvalekalle; -staatiline viga;  - ülereguleerimine; - aeg mille vältel protsess praktiliselt lõppeb;  sumbuvus

Integraal kriteeriumid

Kvaliteedi määramiseks suurema osatähtsuse omavad ja . Neid mõlemaid näitajaid saab arvestada korraga kui võtame integraali reg. protsessist. See integraal annab pindala, mis on selle kõvera all.

Kui , siis võib arvata, et süsteemid on võrdsed kvaliteedi järgi.

ARS süsteemide korrektsioon.

Kui süsteemi kvaliteet ei vasta nõuetele, siis selle parandamiseks viiakse sisse korrektsioon s.t. pannakse lisaelemendid või skeemi muudatusi, selleks et suurendada süsteemi täpsust. Tavaliselt kui süsteemil stab. varud amplituudi ja baasi järgi on väikesed, siis süsteemi kvaliteet on halvem, sellepärast et suureneb max. kõrvalekalle regul. protsessi käigus ja pikeneb regul. aeg. ARS saab korrigeerida järgmiselt:

1. jada korrektsioon, sel juhul reguleerimiskontuuri sisse pannakse jadamisi dif. lüli. Sellel lülil on positiivsed faasinihked ja sellega kompenseeritakse süsteemi neg. faasi nihkeid ja üldine faasinihe väheneb ja süsteemi stabiilsus paraneb ja sellega paraneb ka täpsus, kvaliteet.

2. Rööpkorrektsioon, sel juhul korrigeerivad lülid lülitatakse rööbiti korrigeerivate lülidega. Võib olla otseühendus ja vastuühendus.

V t. joonist : siit on näha, et inertne lüli sellise ühendusega on muudetud dif. lüliks ja dif. lülil on posit. faasi nihke nurgad mis kompenseerivad neg. faasinihke nurgad.

Kui süsteemis on 2 integreerivat lüli, siis nad kohe annavad -180 faasinurga ja süsteem on kindlalt ebastabiilne ja neid on vaja tingimata haarata tagasisidega, et süsteem saaks stabiilseks. Sellist tagasisidet, kus tagasiside elemendiks on element K nim. jäigaks tagasisideks. Selline tagasiside tegutseb nii staatilises kui dünaamilises režiimis. Kui tagasiside ahelas kasutatakse dif. lüli, siis sel juhul see tagasiside ei tegutse staatilises režiimis vaid tegutseb ainult dünaamilises režiimis ja sellist tagas. nim. elastseks tagas. selline tagas. hakkab toimuma ainult siirdeprotsessi jooksul ja sel ajal ta stabiliseerib süsteemi tööd. Kui tagas. ahelasse panna inertne lüli, siis sellist lüli nim. inertseks lüliks