Diferentsiaalvõrrand.

Diferentsiaal võrrand kirjeldab dünaamilise protsessi, mis kulgeb elementides ja diferentsiaal võrrandi lahend näitab kuidas muutub väljundsignaal aja vältel.

A_n*dX_Vⁿ/dtⁿ + A_n-1*dX_V^n-1/dt^n-1 +…+ A₁*dX_V/dt + A₀*X_V = B_m*dX_S^m/dt^m + B_m-1*dX_S^m-1/dt^m-1 +….+

+ B₁*dX_S/dt + B₀*X_S

ⁿ – väljundsignaali kõrgem tuletis, millega määratakse diferentsiaalvõrrandi kõrgem järk

A_{n jne} – koefitsiendid

X_{V – väljundsignaal}

T – aeg

M – sisendsignaali kõrgem tuletis.

Vasakul on väljundsignaal ja tema tuletis, paremal sisendsignaal ja tema tuletis. Kui diferentsiaal võrrandid muutujad on 1 astmes, siis sellist võrrandit nimetatakse lineaarseks. See võrrand kirjeldab dünaamilist protsessi lineaarses süsteemis. Kui võrrandi parem osa ei ole võrdne nulliga, siis sellist võrrandit nimetatakse mittehomogeenseks. See võrrand kirjeldab dünaamilisi protsesse, mis kulgevad süsteemi sisendsignaali pideval mõjutamisel. See tähendab, et sel juhul tekib süsteemis sund liikumine.

Kui diferentsiaal võrrandi parem osa on võrdne nulliga, siis selline võrrand on homogeenne. Selline võrrand kirjeldab süsteemi vaba liikumist, s.t. süsteemile oli antud algmomendil impulss, millega ta oli välja viidud tasakaalust ja edasi toimub süsteemi vaba liikumine.

Selleks, et leida, kuidas muutub väljundsignaal aj vältel tuleb lahendada diferentsiaalvõrrand. See on raske, eriti kui neil on suurema järguline diferentsiaalvõrrand. Lahendamise kergendamiseks on välja töötatud abimeetodid. Üks nendest on operaatormeetod.

Ajakarakteristikud.

Kasutatakse automaatikas sellepärast, et neid saab kergesti üles võtta ja määrata kõik vajalikud staatilised ja dünaamilised parameetrid. AK näitab, kuidas muutub väljundsignaal ajavältel sisendsignaali muutumise korral. Neid karakteristikuid võib määrata lihtsalt ja selleks on vaja sisendisse anda muutuv signaal. Praktikas kasutatakse kahte standardset sisendsignaali:

1. Ühikhüpe – sellele vastab siirdekarakteristik

Siirde karakteristiku järgi saab määrata kõiki uuritavaid objekti parameetreid. Kuid nende määramine võtab mõnikord palju aega( kui objekt on vaga suur) ja see võib rikkuda tehnoloogilist protsessi. Kui suures ahjus üles võtta siirdekarakteristikut, siis selleks on vaja mitu tundi ja see lülitab ahju tootmisprotsessid välja, selle vältimiseks kasutatakse impulsskarakteristikut.

Xs=

2. Impulsssignaal – sel juhul ei anta sisendisse mitte hüpe vaid impulss. Sellele vastavat väljundsignaali muutumist ajas nim. impulsskarakteristikuks.

Impulsskarakteristik on lühiajaline st. tema ülesvõtmiseks kulutatakse vähem aega. Selle järgi aga ei saa määrata kõiki vajalikke parameetreid, kuid selle järgi võib konstrueerida siirde karakteristiku, mis võimaldab määrata kõiki parameetreid.

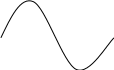
Sageduskarakteristik.

Xs

Väga laialdaselt kasutatakse tehnikavaldkonnas. Süsteemide analüüsimiseks, sünteesimiseks ja arvutamiseks. Praktikas on teda lihtne üles võtta, selleks antakse sisendisse sinusoidaalne signaal mille sagedust saab muuta. Kui sisendsignaali muutub, siis sellest muutuvad väljundsignaali parameetrid, kui sagedus suureneb, siis väljundsignaali amplituud väheneb ja faasinihkenurk sisend ja väljund signaali vahel suureneb.

Xs Xv

Xv



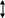
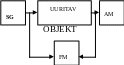
SG - sisendsignaali generaator Xsm – sisend signaali amplituud

AM – amplituudi mõõtja Xvm – väljund signaali amplituud

FM – faasimõõtja  - faasinihkenurk Xs ja Xv vahel

Sagedusfunktsioon:

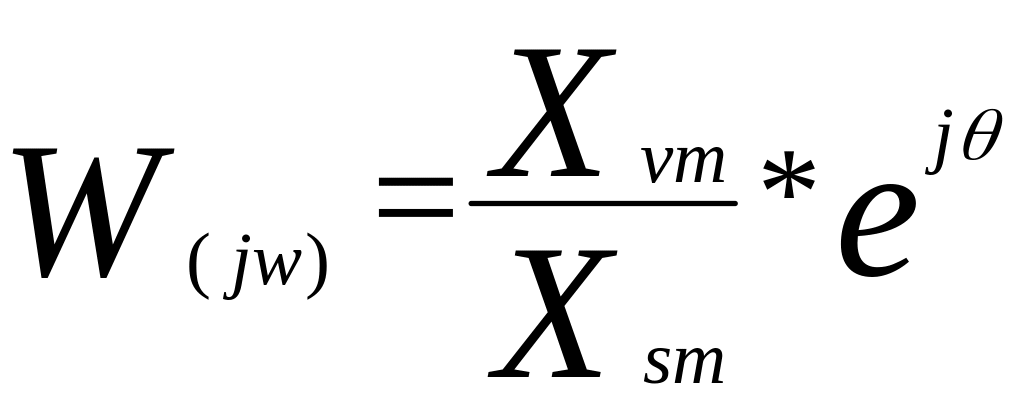
Sinusoidaalsed suurused on vektor suurused ja kahe vektori Xv ja Xs suhe on ka vektor st. sagedusfunktsioon on vektoriaalne suurus. Selle saab määrata tema pikkusega ehk mooduliga ja nurgaga. Sagedusfunktsiooni moodul sõltub sagedusest ja seda sõltuvust nim. amplituudsagedus karakteristikuks

[ |w|=F()].Sagedusfunktsiooni argument sõltub sagedusest ka seda nim. faasikarakteristikuks =f() –FSK.

ASK