5.3. Страховий запас і рівень обслуговування клієнта

Логістичні процеси, як і інші суспільно-господарські процеси, підлягають дії випадкових чинників, через що називаються стохастичними процесами. Отже, ефект управління цими процесами є не лише результатом свідомого формування тими, хто приймає рішення, але також - у більшому або меншому ступені -випадкової події, прояв і силу впливу якої неможливо передбачити. Тобто домінуючою ситуацією під час прийняття менеджерських рішень є непевність. Внаслідок цього з'являються помилки, які супроводжують усі прогнози, необхідні для планування будь-якого виду діяльності.

Спочатку необхідно визначити основні причини згаданої непевності. Ними є саме природа, а також природне право людини на свободу вибору. Незважаючи на вдосконалене прогнозування погоди, часто нас очікують непередбачувані події через природні катаклізми: зливи, повені, снігові бурі тощо порушують графіки поставок і виробництва, що негативно впливає на подальші ланки у логістичних ланцюгах. Своєю чергою, основне право людини на свободу вибору спричиняє те, що не вдається безпомилково спрогнозувати її поведінку і рішення, а, отже, наприклад, момент виникнення і ступінь попиту на певний товар. Це не було можливим навіть за попередньої адміністративно-командної системи, а тим більше за ринкової економіки, в якій головну роль відведено споживачу. До цієї категорії причин (людські рішення, їхня відсутність, помилки тощо) можна віднести також аварії машин, страйки, блокади доріг або прикордонних переходів тощо.

Прагнучи досягти успіхів на ринку, підприємства змушені забезпечувати відповідний рівень логістичного обслуговування клієнта, вважаючи це завдання першочерговим серед решти завдань логістики. Своєю чергою, найважливішим елементом цього обслуговування є доступність товарів з запасу, тобто готовність до термінового задоволення виявленого попиту. Клієнта, який шукає конкретний товар, не задовольнять принади іншого магазину у вигляді дегустацій, оригі­нальних рекламних звернень, якщо потрібного товару там немає. Незадоволений клієнт піде до конкурента.

Часто рятують ситуацію під час непередбачуваних подій резерви. Це як на війні, коли "командир, який не має резерву, перестає бути командиром, оскільки не може впливати на перебіг подій". Особливим випадком резервів є страхові запаси (англ. - safety stocks) матеріалів, готової продукції тощо, які називають також резервними, або буферними запасами. їх будують на стиках логістичних шляхів, збільшуючи поточні запаси. Якщо таких запасів немає, це може призвести до: виникнення більшого попиту, ніж його прогнозована середня величина під час реалізації замовлення (рис. 5.2, а), довшого періоду реалізації замовлених поставок, ніж середній (рис. 5.2, б) або одночасного прояву обох цих тенденцій.

Отже, страхові запаси мають - з прийнятим ступенем ймовірності запобігати таким некорисним подіям, а, отже, гарантувати закладений рівень обслуговування клієнта (рис. 5.3).

Підтверджують правильність нагромадження відповідного страхового запасу результати, отримані таким методом математичної статистики, як естимація (оцінювання) параметрів у невідомій основній популяції. Адже йдеться у цьому випадку про конструювання так званого проміжку довіри² для середнього значення на основі статистичної вибірки. Облікований продаж товару у встановлених періодах (наприклад, тижнях) - це своєрідна статистична вибірка, яка від "нормальних" вибірок цього типу відрізняється тим, що принципового значення в ній набуває хронологія появи зафіксованих величин, адже це стосується часового ряду. Це дає змогу під час прогнозування його середньої величини виокремити такі важливі складові ряду, як зміни трендів і сезонні коливання.

² Тобто проміжку, який з великою попередньо прийнятою ймовірністю покриває значення оцінюваного параметра - у цьому випадку прогнозованого, середнього попиту під час реалізації замовлення.

Для нормального (стандартного) розподілу існують такі верхні межі проміжку довіри :

в якому у - прогноз середнього попиту під час одиничного періоду (наприклад,

тижні); L - середній зареєстрований період реалізації замовлень, поданий у прийнятих одиничних періодах; S - прогноз стандартної похибки прогнозу, яка є відповідником стандартного відхилення з вибірки і визначається за формулою:

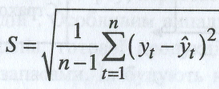
де y_t - величина попиту в періоді t; y_t - прогноз попиту під час того самого періоду; п - кількість аналізованих прогнозів; к - коефіцієнт кратності, тобто величина, яка виникає з прийнятого рівня обслуговування клієнта; для нормального стандартного розподілу справедливі такі закономірності (див. табл. 5.1.)

- значенню к = 1 відповідає 84,1-відсоткова ймовірність задоволення попиту (тобто 84-відсотковий рівень обслуговування клієнта у разі закладання статистичної стабільності);

- значенню к = 2 відповідає 97,4-відсоткова ймовірність задоволення попиту (приблизно 98-відсотковий рівень обслуговування клієнта);

- значенню к = 3 відповідає 99,9-відсоткова ймовірність задоволення попиту (практично 100-відсотковий рівень обслуговування клієнта).

³ Принциповість застосування нормального розподілу випливає з так званого центрального граничного твердження, за яким якщо вибираємо и-елементну вибірку з популяції з середнім (і і закінченим стандартним відхиленням о, то розподіл середнього ц з достатньо великої (ЗО і більше елементів) вибірки прямує до нормального розподілу з середнім ц. і стандартного відхилення о: Vn. За менших вибірок загалом використовуємо розподіл t-Стьюдента.

⁴ Адже йдеться лише про ситуації, в яких фактичний попит, можливо, перевищить правий кінець такого проміжку.

Складова - це згадуваний страховий запас, який створюють на випадок виникнення за середній період реалізації замовлень попиту більшого ніж прогнозований.

Рівень обслуговування клієнта можна визначити як здатність до задоволення попиту, заявленого клієнтами, з доступного запасу. За цим підходом вважатимемо його ймовірністю того, що впродовж циклу запасу дефіциту не виникає. Це має назву рівень обслуговування впродовж запасу (англ. — cycle-service level). На рис. 5.4 наведено залежності trade-off між рівнем обслуговування клієнта і величиною страхового запасу.

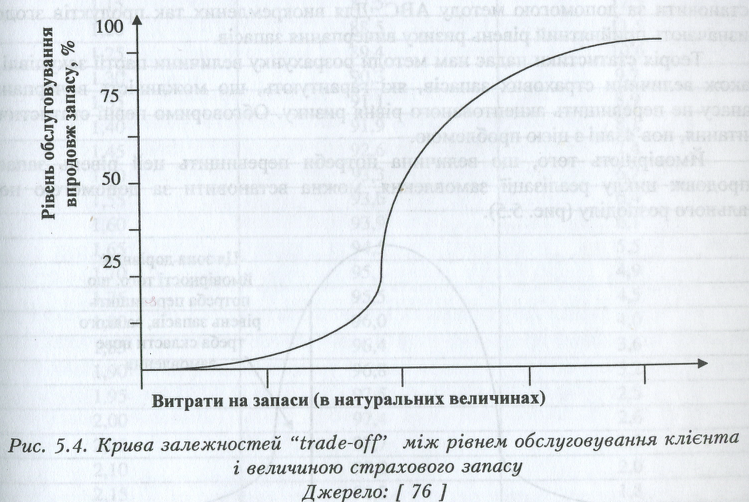
З рис. 5.4 видно, що рівень обслуговування клієнта можна підвищити збільшуючи витрати на запаси. Можна зробити такі висновки:

• кожна додаткова витрата на запас даного товару, а точніше, збільшенні страхового запасу завжди покращує обслуговування клієнта;

• і навпаки, вищий рівень обслуговування клієнта вимагає утримуванні більших страхових запасів, а отже, збільшення витрат на запаси;

• досягнення 100-відсоткового рівня обслуговування клієнта через максимізацію рівня запасів є неможливим, оскільки утримування високого рівня страхо­вих запасів усіх товарів малоефективно і пов'язано із занадто високими витратами.

За системою just-in-time рівень запасів низький або нульовий, а виконати цей постулат можна, якщо ненадійність поставок є винятком. Страховий запас є чинником, який генерує додаткові витрати і як такий має бути зменшений до нуля.

Якщо не вдається добитися 100-відсоткової надійності поставок, треба утримувати страхові запаси. Високий рівень обслуговування клієнта щодо кожного товару є неекономічним, оскільки спричиняє занадто високі надбавки на запаси. Продукти, які характеризуються високими витратами вичерпання запасів, можна встановити за допомогою методу ABC. Для виокремлених так продуктів згодом визначають прийнятний рівень ризику вичерпання запасів.

Теорія статистики надає нам методи розрахунку величини партії закупівлі, а також величини страхових запасів, які гарантують, що можливість вичерпання запасу не перевищить акцептованого рівня ризику. Обговоримо певні статистичні питання, пов'язані з цією проблемою.

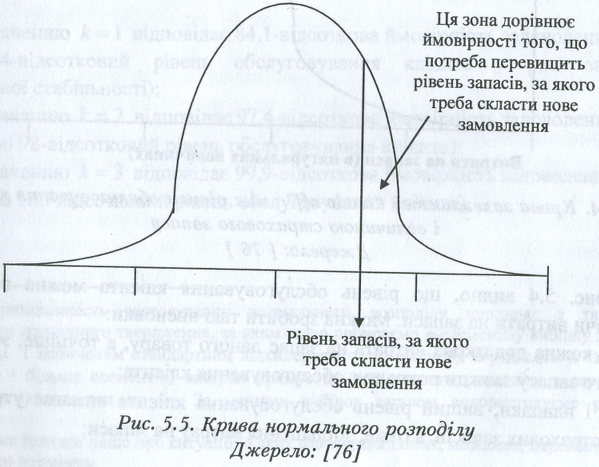
Ймовірність того, що величина потреби перевищить цей рівень запасів впродовж циклу реалізації замовлення, можна встановити за допомогою нор­мального розподілу (рис. 5.5).

Таблиця 5. 1

Таблиця ймовірностей за нормального розподілу

Кратність середньоквадратичного відхилення	Рівень обслуговування клієнта (Х(%)	Ймовірність вичерпання запасу (1-а) (%)
1	2	3
1,00	84,1	15,9
1,05	85,3	14,7
1,10	86,4	13,6
1,15	87,5	12,5
1,20	88,5	11,5
1,25	89,4	10,6
1,30	90,3	9,7
1,35	91Д	8,9
1,40	91,9	8,1
1,45	92,6	7,4
1,50	93,3	6,7
1,55	93,6	6,4
1,60	93,9	6,1
1,65	94,5	5,5
1,70	95,1	4,9
1,75	95,5	4,5
1,80	96,0	4,0
1,85	96,4	3,6
1,90	96,8	3,2
1,95	97,5	2,5
2,00	97,4	2,6
2,05	97,7	2,3
2,10	98,0	2,0
2,15	98,2	1,8
2,20	98,4	1,6
2,25	98,6	1,4
2,30	98,8	1,2
2,35	98,9	ІД
2,40	99,1	0,9
2,45	99,2	0,8
2,50	99,3	0,7
2,55	99,4	0,6

Продовження табл. 5.1

1	2	3
2,60	99,5	0,5
2,65	99,6	0,4
2,70	99,7	0,3
2,75	99,7	0,3
2,80	99,7	0,3
2,85	99,8	0,2
2,90	99,8	0,2
3,00	99,9	0,1

Чимало джерел із статистики подають таблиці нормального розподілу (див. табл. 5.1). Для розподілу Пуассона та експонентного розподілу коефіцієнт кратності середньоквадратичного відхилення наведено у табл. А ситуаційної вправи 2. Щоб скористатися ними, ми маємо знати середнє і стандартне відхилення потреби в процесі одного циклу реалізації замовлення. Ці величини можна розрахувати за такою процедурою:

• серед зареєстрованих замовлень, висланих постачальнику певного товару, треба випадково вибрати певну кількість цих замовлень (найкраще близько 30);

• треба знайти дату складання кожного замовлення у вибірці, а також дату поставки замовлених продуктів; на підставі записів, які стосуються складських станів, розрахувати потребу в аналізованому товарі між цими двома датами;

• розрахувати середню потребу (Z_s) впродовж циклу реалізації замовлення:

де х - сума потреб, заявлених під час певного періоду; п - кількість циклів реалізації замовлень;

• розрахувати стандартне відхилення для цієї потреби:

(2)

(ці значення можна розрахувати також за допомогою калькулятора або електронної таблиці);

• знайти у таблиці ймовірностей потрібний рівень запасів, за якого треба складати повторне замовлення (табл. 4.1).

Проілюструємо розрахунок страхових запасів за традиційними системами управління запасами, виходячи з таких вихідних даних:

річний попит на товар Р_річн;

витрати опрацювання одного замовлення С_зсш;

вартість одиниці запасу Cj;

питомі річні витрати утримання запасів (% від вартості запасу, г_уз );

час реалізації замовлення L;

розрахунковий час планового періоду Т.

Більшість відомих методів управління запасами можна віднести до одного з двох головних методів: постійної величини замовлення, а також періодичного перегляду стану запасів.

1. За методом постійної величини замовлення (модель рівня замовлення, система складання повторного замовлення за певного рівня запасів, або система "двох скринь") контролюють запаси простим, нематематичним способом. За цим методом запас певного блага ділять на "дві скрині", потребу в якому задоволь­няють спочатку з запасу у першій скрині. Рівень запасів, який сигналізує керівнику складу про необхідність складання повторного замовлення і виставлення заявки потреби настає в момент повного випорожнення першої скрині. Отже, величина, яку замовляють, є постійною (її можна встановити за допомогою моделі Q_opt ).

Для розрахунку страхового запасу припускаємо, що попит на продукцію має нормальний розподіл з середнім значенням попиту у для досліджуваного проміжку часу і з середньоквадратичним відхиленням S,. Якщо час на виконання замовлення є постійним і становить L, попит протягом цього часу нормально розподілений із середнім значенням L ху. Попит протягом виконання замовлення має дисперсію S_t XL і середньоквадратичне відхилення S_tХл/Z.

попит за один період має середнє значення у і дисперсію S,²;

попит за два періоди має середнє значення 2у і дисперсію 2S} ; попит за три періоди має середнє значення Зу і дисперсію 35,²; попит за п ху періодів має середнє значення п ху і дисперсію nxS/

Оскільки обсяг страхового запасу Z_cmpax залежить від рівня обслуговування споживачів а, його величину розраховують за формулою:

Обсяг страхового запасу = к х середньоквадратичне відхилення попиту за період L

(3)

де S_ty[L - середньоквадратичне відхилення часу на виконання замовлення; к-кратність середньоквадратичного відхилення, яку визначають за допомогою статистичних таблиць, наведених у табл. 5.1. додатку А.

Після розрахунку оптимального обсягу замовлення Q₀„_m, страхового обсягу запасів Z_cmpax за різних рівнів обслуговування а визначають витрати утримання страхового запасу за формулою:

За теорією управління запасами верхня границя проміжку довіри А ста­новить так званий рівень замовлення⁵ (re-order point). Треба підкреслити, що запас безпеки в іншій класичній моделі управління запасами (постійного циклу замовлення) утворюється для довшого періоду, який охоплює також цикл замовлення. Варто зауважити, що у цій формулі прийнято постійний період реалізації замовлень L . У випадку великої змінності цього періоду формула для розрахунку страхового запасу є складнішою.

2. Метод періодичного перегляду стану запасів (модель циклу замовлення, система управління запасами з постійним циклом замовлення). Сутність моделі циклу замовлення полягає в регулярному (через однакові проміжки часу) попов­ненні запасів до стабільного максимального рівня. В умовах коливання попиту залишок запасів на складі в кінці кожного циклу поставки змінюватиметься залеж­но від інтенсивності попиту протягом цього циклу, тому величина замовлення теж буде змінним параметром і визначатиметься різницею між максимальним (розрахунковим) запасом і залишком запасів на момент формування замовлення. Тривалість періодів або проміжків часу, які проходять між переглядами рівня запасів, залежить від значення запасу певного блага, а також від витрат на

Принципи поповнювальних закупівель у випадку застосування моделі рівня замовлення, як і інших моделей, можна знайти у праці: Крикавський Є.В. Логістика для економістів [15].

утримання цього запасу. Після кожного перегляду складають (у разі потреби) замовлення зі змінною величиною, за якою можна збільшити рівень запасів до встановленого максимального рівня (часом це називають "рівнянням до максимуму").

Графічно це подано на рис. 5.6.

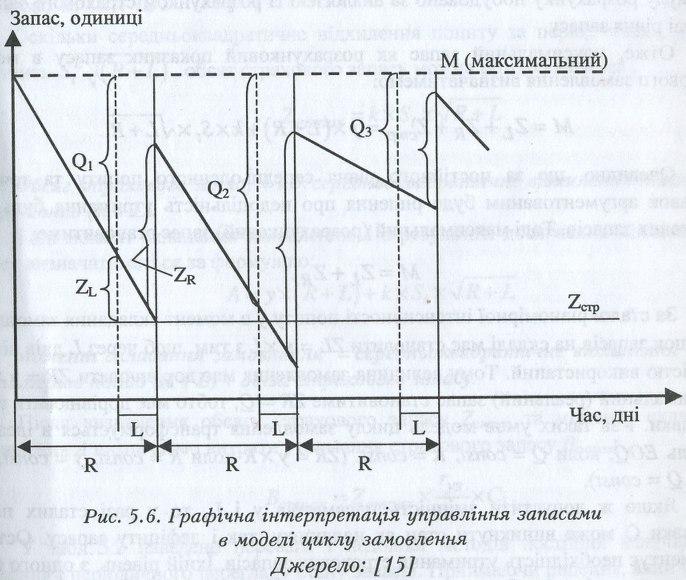
Оскільки термін виконання замовлення має реальний час L, то замовлення необхідно подати в час (R - L) за L днів до поставки з тим, щоб реалізувати її в розрахунковий час R. Тому величина замовлення має бути такою, щоб максимальний запас міг покрити:

• попит на період реалізації замовлення L: ZL = у х L;

• попит протягом наступного циклу R: ZR = у х R, де у - очікуваний (розрахунковий) середньоденний попит; L, R - відповідно тривалість замовлення і Цикл поставки;

• ймовірний додатковий попит, викликаний зростанням інтенсивності попиту понад розрахункову величину у протягом періоду виконання замовлення і наступного циклу поставки, запізненням поставки, пошкодженням частини запасу на складі і в дорозі, покривають який із страхового запасу:

Формулу розрахунку побудовано за аналогією із розрахунком страхового запасу в моделі рівня запасу.

Отже, максимальний запас як розрахунковий показник запасу в момент чергового замовлення визначатимемо:

(5)

Очевидно, що за постійного рівня середньоденного попиту та точності поставок аргументованим буде рішення про недоцільність утримання будь-яких страхових запасів. Тоді максимальний (розрахунковий) запас становитиме:

M = Z_L + Z_R. (6)

За сталої рівномірної інтенсивності попиту у в момент складання замовлення залишок запасів на складі має становити ZL-y xL з тим, щоб через L днів він був повністю використаний. Тому величина замовлення має дорівнювати ZR = y xR, a максимальний (реальний) запас становитиме ZR = Q, тобто має дорівнювати партії поставки. І за таких умов модель циклу замовлення трансформується в ідеальну модель EOQ, коли Q = const, R = const, (ZR = у xR коли R = const, у = const, то і ZR = Q = const).

Якщо ж допустити змінність параметрів у і L, то у разі сталих партій поставки Q може виникнути стан як надлишку, так і дефіциту запасу. Останнє аргументує необхідність утримання страхових запасів. їхній рівень, з одного боку, визначається рівнем обслуговування параметрами відхилень у і L, а, з іншого, співвідношенням питомих витрат утримання запасів і питомих витрат вичерпання запасів, що акумульовано в показнику кратності стандартного відхилення k .

Припускаємо, що попит на продукцію має нормальний розподіл з середнім значенням попиту у для досліджуваного проміжку часу і середньоквадратичним відхиленням S_t. Якщо час на розміщення замовлення R та виконання замовлення L є величинами постійними, а попит протягом цього часу нормально розподілений із середнім значенням у, то попит протягом виконання замовлення набуває таких значень:

• попит за один період має середнє значення у і дисперсію S_t ;

• попит за два періоди має середнє значення 2у і дисперсію 2S_t ; тоді

• попит за період, що перевищує (R + L), має середнє значення y(R + L) і 2 дисперсію S_t (R + L) .

Оскільки середньоквадратичне відхилення попиту за період понад (R + L) становить обсяг страхового запасу можна розрахувати так:

(7)

або Обсяг страхового запасу = к хсередньоквадратичне відхилення попиту за період понад (R + L).

Тоді момент складання замовлення А в результаті досягнення мінімального запасу визначатиметься за формулою:

(8)

або момент складання замовлення - середньоквадратичне відхилення попи­ту, за період понад (R + L) + обсяг страхового запасу.

Після визначення обсягу страхового запасу Z_cmpax та моменту складання замовлення А визначаємо витрати утримання страхового запасу В_страх:

У табл. 5.2 наведено переваги і недоліки методів постійної величини за­мовлення і періодичного перегляду стану запасів. Таблиця 5.2 Порівняння переваг і недоліків методів постійної величини замовлення і періодичного перегляду стану запасів

Приймаючи рішення, який із двох обговорених методів управління запасами вибрати, варто врахувати такі аспекти:

• метод постійної величини замовлення найкраще застосовувати у випадку запасів, які споживаються регулярно;

• метод періодичного перегляду стану запасів є найвідповіднішим тоді, коли замовлення поповнення складають у постачальників і реалізують упродовж регулярних проміжків часу (наприклад, кожного дня, кожного місяця) або якщо велику кількість запасів різних позицій замовляють в одного постачальника, який Доставляє їх у той самий час.