Лабораторна робота № 5 Тема: випадкові сигнали.

Мета: ознайомитися з випадковими сигналами, набути навиків розрахунку їх характеристик.

Теоретичні відомості

На відміну від детермінованих сигналів, форма яких відома точно, миттєві значення випадкових сигналів наперед не відомі і можуть бути передбачені лише з деякою ймовірністю. Характеристики таких сигналів є статистичними. Математична модель випадкового сигналу, що змінюється в часі, називається випадковим процесом. До прийому випадковий процес слід розглядати як сукупність (ансамбль) функцій часу , які підпорядковуються деякій спільній для них статистичній закономірності. Одна із цих функцій, що стала відомою після прийому сигналу, називається реалізацією випадкового процесу. Ця реалізація є вже не випадковою, а детермінованою функцією часу.

Математична модель випадкового процесу – це опис можливих реалізацій випадкового процесу із вказанням відносної частоти їх появи.

Імовірнісні характеристики випадкових процесів

Нехай випадковий процес задано ансамблем реалізацій . Вибравши довільний момент часу , зафіксуємо значення, що приймаються всіма реалізаціями: . Сукупність цих значень утворює одновимірний переріз випадкового процесу і є випадковою величиною . Основними характеристиками цієї випадкової величини є:

1. Щільність ймовірності – ймовірність потрапляння значення випадкового процесу у безконечно малий окіл навколо точки х.

2. Функція розподілу ймовірності – ймовірність того, що в момент часу значення випадкового процесу не перевищують х:

;

. (1)

Ймовірність потрапляння значення випадкового процесу у проміжок рівна

.

3. Математичне очікування 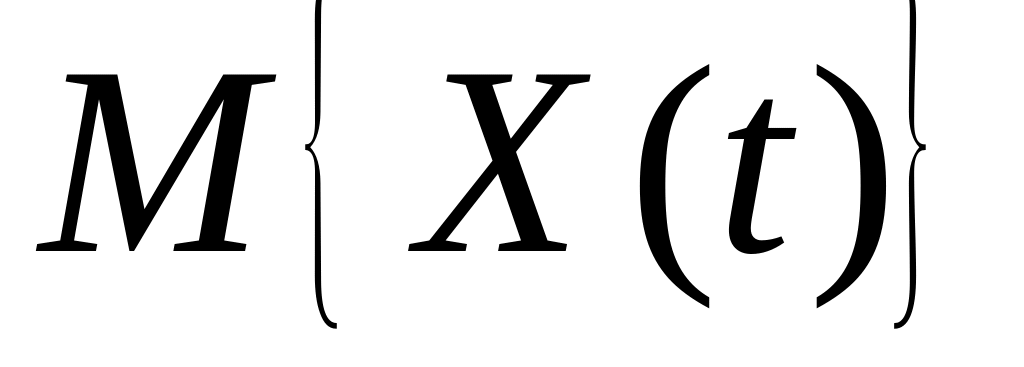– теоретична оцінка середньозваженого значення випадкового процесу у момент часу t:

. (2)

4. Дисперсія – середня потужність відхилень значень випадкового процесу від його середнього значення:

. (3)

5. Середнє квадратичне відхилення – амплітудна міра розкиду випадкового процесу в момент часу t відносно математичного очікування:

. (3)

Щільність імовірності сигналу можна знайти експериментально, розглядаючи деяку достатньо велику реалізацію (або ансамбль реалізацій) випадкового процесу. Одним із методів вимірювання щільності ймовірності є гістограмний метод. Розглянемо його детальніше.

Гістограмний метод оцінювання густини ймовірності

Сутність гістограмного методу вимірювань густини ймовірностей зручно пояснювати на прикладі неперервної випадкової величини (ВВ) . Розділимо весь діапазон значень ВВ на інтервали («розряди») довжиною і підрахуємо кількість значень , що приходяться на кожний -й інтервал. Це число поділимо на загальну кількість спостережень і таким чином знайдемо частоту, що відповідає даному інтервалу:

. (4)

Сума частот для всіх інтервалів, очевидно, повинна дорівнювати одиниці.

Побудуємо таблицю, в якій приведені інтервали в порядку їх розташування вздовж осі абсцис, й відповідні частоти. Ця таблиця називається статистичним рядом. Приклад статистичного ряду, де позначені інтервали значень ВВ наведено у табл. 1.

Таблиця 1

	[-4;-3)	[-3;-2)	[-2;-1)	[-1;0)	[0;1)	[1;2)	[2;3)	[3;4]
	6	25	72	133	120	88	46	10
	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020

Статистичний ряд часто оформлюють у вигляді графіка, котрий називають гістограмою (рис. 1). Очевидно, при збільшенні кількості дослідів можна зменшити розмір інтервалів ; при цьому гістограма буде все більше наближатися до істинної щільності ймовірності величини .

Користуючись даними статистичного ряду, можна наближено побудувати й статистичну функцію розподілу (тобто оцінку інтегрального закону розподілу) величини (рис. 2).

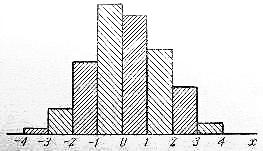
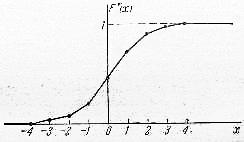
Рис. 1 Гістограма розподілу Рис. 2 Функція розподілу

Розглянемо тепер задачу оцінювання одновимірної щільності ймовірностей ергодичного стаціонарного випадкового процесу (СВП) за його єдиною реалізацією . Пов’язуючи цю задачу із попередньою, неважко бачити, що значення у фіксований момент часу можна трактувати як значення якоїсь випадкової величини .

Позначимо час перебування ергодичного (відносно вимірювання густини ймовірностей) СВП в -околі значення (рис. 3). Тоді оцінку імовірності потрапляння СВП в -окіл значення можна представити у вигляді відносного часу перебування:

, (5)

де

,

- час перебування СВП в -околі значення в -тій часовій ділянці.

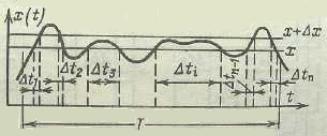
Рис. 4

Оцінка щільності при цьому може бути представлена у вигляді:

. (6)

Середнє значення оцінки (6):

. (7)

Неважко бачити, що через скінченні розміри розряду оцінка (6) зміщена:

. (7)

Вираз для зміщення оцінки (6):

.

Якщо границі інтервалу симетричні відносно точки , тоді

,

і вираз для зміщення спрощується (в подальшому будемо використовувати саме цей вираз):

. (8)

Дисперсія оцінки щільності ймовірності:

, (9)

де .

Таким чином, справедливі наступні висновки.

Висновок 1: При плануванні експерименту з вимірювань щільності потрібно пам’ятати, що в руках експериментатора є всього два «важелі» для управлення точністю вимірювань: величина інтервалу та довжина відрізку реалізації (або, що одне й те ж, - кількість відліків );

Висновок 2: при фіксованому зміщеність оцінки можна зменшити шляхом зменшення величини інтервалу ;

Висновок 3: при фіксованому дисперсію оцінки можна зменшити шляхом збільшення ;

Висновок 4: вимога збільшення точності вимірювань щільності при фіксованому зводиться до вимоги змінювати величину інтервалу ; при цьому вимоги до є суперечливими: зі збільшенням дисперсія зменшується, але одночасно з цим збільшується зміщеність; тому для фіксованого можна ставити задачу про пошук оптимального , що мінімізує повну похибку вимірювань:

. (10)

Висновок 5: на відміну від зміщення, дисперсія оцінки залежить не тільки від , але й від : при фіксованому значенні дисперсія оцінки обернено пропорційна об’єму вибірки , тобто тривалості інтервалу спостереження .

Висновок 6: узагальнюючи результати, приходимо до висновку про доцільність погодженого вибору параметрів і :

.

Розглянемо деякі види випадкових процесів та їх реалізацію в пакеті MathCAD.