Енергетичні спектри сигналів

Скалярний добуток сигналів та визначається таким чином:

.

Якщо сигнали однакові, , то скалярний добуток переходить в енергію сигналу

.

Зв’язок між скалярним добутком сигналів та їх спектральними щільностями можна встановити за допомогою узагальненої формули Релея.

Узагальнена формула Релея

Припустимо, що розглянуті вище сигнали та , які входять до формули (1), задані своїми спектральними щільностями:

,

. (16)

Якщо розглянуті сигнали описуються дійсними функціями часу, тоді

(17)

Одержане співвідношення називають узагальненою формулою Релея. Трактування цією формули таке: скалярний добуток двох сигналів пропорційний скалярному добутку спектральних щільностей.

Дійсна функція

, (18)

дозволяє виразити скалярний добуток сигналів та таким чином:

. (19)

Функцію називають взаємним енергетичним спектром сигналів та . Формула (19) розкриває “тонку структуру” зв’язку двох сигналів. У формуванні взаємної енергії сигналів різні ділянки їх спектра грають неоднакову роль: найбільший вклад забезпечують ті частотні ділянки, в яких спектри сигналів перекриваються.

Узагальнена формула Релея, представлена у вигляді (19), дозволяє знайти шлях зменшення міри зв’язку між сигналами, досягаючи в граничному варіанті їх ортогональності. Для цього один з розглянутих сигналів треба перетворити в особливій фізичній системі, яка не пропускає на вихід ті спектральні компоненти сигналів, що знаходяться в межах частотного інтервалу, де взаємний енергетичний спектр найбільший.

Енергетичний спектр сигналу

Спектральне представлення енергії сигналу легко можна отримати як частковий випадок узагальненої формули Релея, якщо в ній сигнали та вважати однаковими.

Формула (18), що виражає спектральну щільність енергії, матиме вигляд:

. (20)

Величина має назву спектральної щільності енергії сигналу або енергетичного спектра.

Формула (19) при цьому записується так:

. (21)

Ця формула констатує важливий результат: енергія будь-якого сигналу може бути представлена як результат додавання вкладів від різних інтервалів частотної осі.

Автокореляційна функція

Автокореляційна функція (АКФ) детермінованого сигналу з кінечною енергією являє собою інтеграл від добутку двох копій сигналу, зміщених одна відносно одної на час τ:

. (10)

Автокореляційна функція вказує на степінь подібності між сигналом і його зміщеною копією: чим більше значення АКФ, тим ця схожість вища. Крім того, автокореляційна функція має такі властивості:

1. Значення АКФ при рівне енергії сигналу:

.

2. АКФ є парною функцією свого аргументу:

.

3. Максимум АКФ спостерігається при ;

4. З ростом абсолютного значення τ АКФ сигналу з кінечною енергією затухає;

5. Якщо сигнал не містить особливостей у вигляді дельта-функцій, його АКФ не може мати розривів.

Приклад 1. Розрахуємо АКФ прямокутного імпульсу, графік якого зображено на рис. 1:

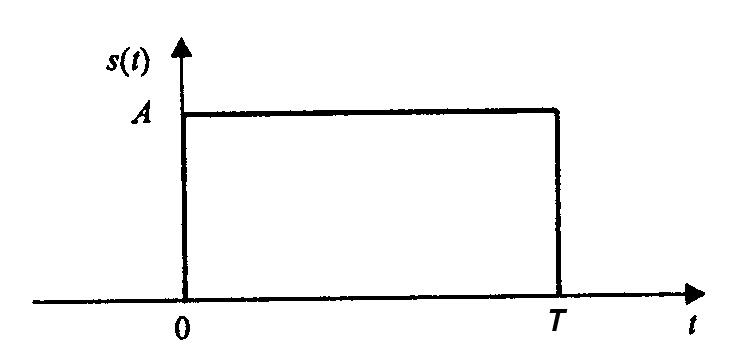
Рис. 1 Прямокутний імпульс

• при :

;

• при :

;

• при :

.

Об’єднуючи результати, можна записати:

Графік АКФ прямокутного імпульсу показано на рис. 2.

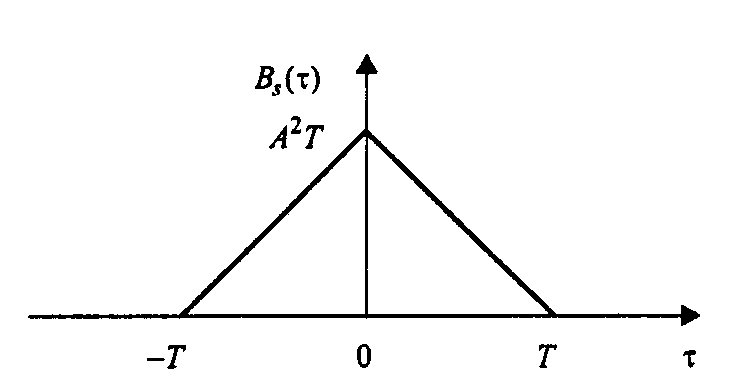
Рис. 2 Автокореляційна функція прямокутного імпульсу

У випадку періодичного сигналу (і взагалі, будь-якого сигналу з безкінечною енергією) використати наведене визначене не можна. Тому АКФ періодичного сигналу з періодом Т обчислюють, усереднюючи добуток зміщених копій у межах одного періоду:

. (11)

Набір властивостей такої АКФ змінюється:

1. Значення АКФ при рівне середній потужності аналізованого сигналу:

;

2. Властивість парності зберігається:

.

3. Максимум АКФ спостерігається при ;

4. АКФ періодичного сигналу є періодичною функцією з тим же періодом, що і сам сигнал: ;

5. Якщо сигнал не містить особливостей у вигляді дельта-функцій, його АКФ не може мати розривів.

Приклад 2. Розрахуємо АКФ гармонійного сигналу з частотою :

.

Обчислюємо кореляційний інтеграл, враховуючи, що період такого сигналу рівний :

.
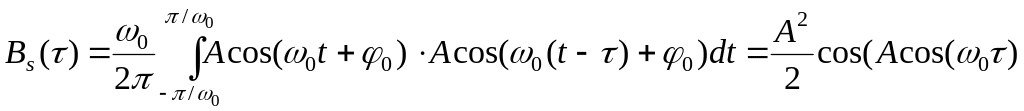