Лабораторна робота № 3 Тема: аналітичний сигнал. Кореляційні функції сигналів.

Мета: вивчити особливості аналітичного сигналу, співвідношення початкового сигналу та сигналу, спряженого до нього, ознайомитися з властивостями перетворення Гільберта, набути навиків розрахунку енергетичних параметрів сигналу та кореляційних функцій.

Теоретичні відомості

Формула Ейлера

,

що представляє гармонічне коливання у вигляді суми двох комплексно-спряжених функцій, наводить на думку, що довільний сигнал , з відомою спектральною щільністю , може бути однозначно записаний як сума двох компонент, кожна з яких містить тільки додатні або тільки від’ємні частоти.

(1)

Назвемо функцію

(2)

аналітичним сигналом, що відповідає дійсному коливанню . Перший з інтегралів у правій частині (1) шляхом заміни змінної перетворюється таким чином:

.

Тому формула (1) встановлює такий зв'язок між сигналами та :

.

Уявна частина аналітичного сигналу

називається спряженим сигналом у відношенні до початкового сигналу .

Проекція аналітичного сигналу на дійсну вісь у будь-який момент часу дорівнює початковому сигналу :

(3)

Спектральна щільність аналітичного сигналу

Знайдемо спектральну щільність аналітичного сигналу , яка дозволяє знаходити , використовуючи зворотне перетворення Фур'є.

На основі (2) можна стверджувати, що ця функція відмінна від нуля лише в області додатних частот:

(4)

Якщо - спектральна щільність спряженого сигналу, то ,внаслідок лінійності перетворення Фур’є,

(5)

Тому рівність (4) буде виконуватись тільки в тому випадку, коли спектральна щільність початкового і спряженого сигналів зв’язані між собою наступним чином:

(6)

Абстрактно можна уявити такий спосіб одержання спряженого сигналу: початкове коливання подається на вхід деякої системи, яка здійснює поворот фаз усіх спектральних компонент на кут в області додатних частот і на кут в області від’ємних частот, не змінюючи їх за амплітудою. Система, яка має такі властивості, називається квадратурним фільтром.

Перетворення Гільберта

Формула (6) показує, що спектральна щільність сигналу є добутком спектру початкового сигналу та функції , тому спряжений сигнал є згорткою двох функцій та , яка є зворотнім перетворенням Фур’є у відношенні до .

Для зручності обчислень представимо функцію у вигляді

.

Тоді

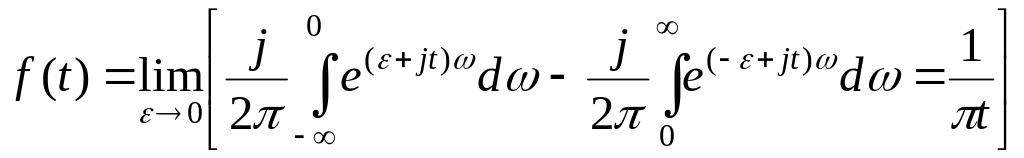
Тоді спряжений сигнал буде зв’язаний з початковим сигналом співвідношенням:

. (7)

Можна поступити інакше: виразити сигнал через , який вважається відомим. Для цього достатньо помітити, що з (6) випливає таке співвідношення між спектральними щільностями:

.

Тому відповідна формула буде відрізнятися від (7) лише знаком.

(8)

Формули (7) і (8) відомі в математиці під назвою прямого та зворотного перетворення Гільберта .

Символічний запис їх такий:

, (9)

Функція - ядро перетворень Гільберта . Оскільки функція має розрив при , то інтеграли у (7) та (8) слід брати до уваги у розумінні головного значення. Наприклад,