Частота Найквіста

Відповідно до теореми Котельникова, гармонічний сигнал може бути адекватно представлений дискретними відліками, якщо його частота не перевищує половини частоти дискретизації (ця частота називається частотою Найквіста):

. (1)

Походження цього обмеження пояснює рисунок 3.

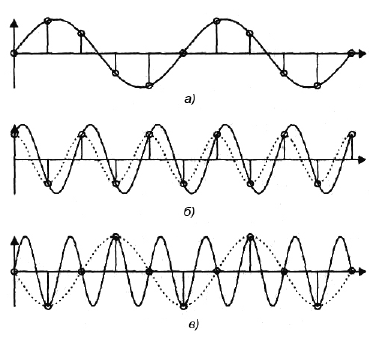
Рис. 3 Дискретизація гармонічних сигналів з різною частотою

Залежно від співвідношення між частотою гармонічного сигналу, що дискретизується, і частотою Найквіста можливі три випадки.

1. Якщо частота гармонічного сигналу менша частоти Найквіста, дискретні відліки дозволяють правильно відновити аналоговий сигнал (рисунок 3, а).

2. Якщо частота гармонічного сигналу дорівнює частоті Найквіста, то дискретні відліки дозволяють відновити аналоговий гармонічний сигнал з тією же частотою, але амплітуда і фаза відновленого сигналу (він показаний пунктирною лінією) можуть бути перекручені (рисунок 3, б). У найгіршому випадку всі дискретні відліки синусоїди можуть виявитися рівними нулю.

3. Якщо частота гармонійного сигналу більша частоти Найквіста, то відновлений по дискретним відлікам аналоговий сигнал (як і в попередньому випадку, він показаний пунктирною лінією) буде також гармонічним, але з іншою частотою (рисунок 3, в). Цей ефект зветься появою помилкових частот (aliasing).

Спектри аналогових і дискретних сигналів

Для опису аналогових і дискретних сигналів у частотній області використовується апарат перетворення Фур'є. Спектром аналогового сигналу називають пряме перетворення Фур'є

. (2)

У свою чергу, відповідно до оберненого перетворення Фур'є

(3)

Передбачається збіжність інтегралів у (2), (3), а також виконання умови при t < 0.

Пара перетворень Фур'є для дискретної часової послідовності має вигляд:

. (4)

. (5)

Таким чином, комплексну функцію називають спектром дискретного сигналу .

У середовищі MathCAD виконання перетворень Фур’є виконується наступними функціями:

1. cfft(A) – виконує дискретне перетворення Фур’є даних комплексного вектора А.

2. icfft(u) – виконує зворотне дискретне перетворення Фур’є даних вектора u, створеного за допомогою функції cfft(A).

Відновлення аналогових сигналів по дискретних відліках

Відновлення аналогового сигналу по його дискретному представленню, тобто послідовності вибірок зводиться до використання різних інтерполяційних процедур.

При виконанні умов, обумовлених теоремою відліків (теоремою Котельникова), операції дискретизації і відновлення взаємно обернені. Відповідно до цієї теореми, якщо аналоговий сигнал має фінітний (обмежений частотою Найквіста ) спектр, тобто такий, що при , то такий сигнал можна однозначно представити послідовністю вибірок , взятих з періодом дискретизації , де , на основі ряду Котельникова

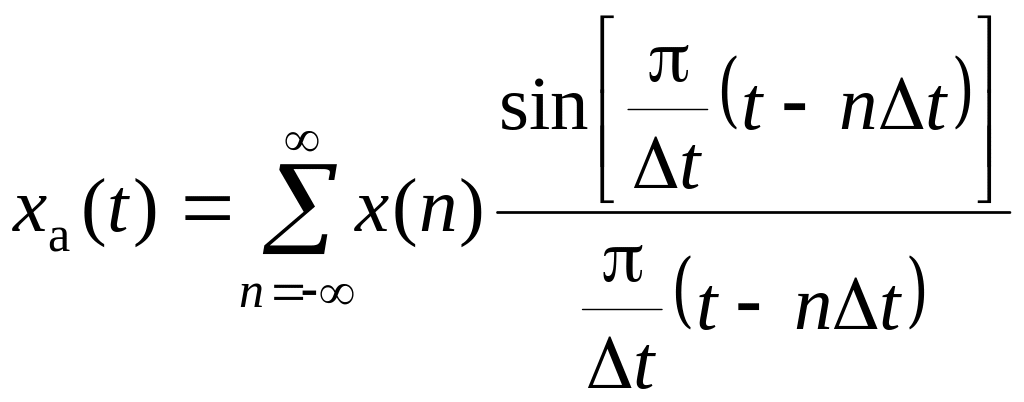. (6)

Спектр послідовності , отриманої в результаті дискретизації з частотою аналогового сигналу , і спектр пов'язані співвідношенням

, (7)

тобто спектр дискретної послідовності дорівнює з точністю множника 1/T сумі спектрів відповідного аналогового сигналу , зміщених по осі частот на всі можливі значення частоти, кратні частоті дискретизації .