2.6. Свойства интегральных сумм

В этом пункте τ = - дробление ограниченного промежутка X = , a < b, образованное набором точек . f – функция, ограниченная на X, а и - её составляющие. Обозначим:

;

.

Используются и другие обозначения, введенные выше.

1. τ) ≤ S (f, τ) ≤ τ).

► Так как ξ_j , то m_j ≤ f (ξ_j) ≤ M_j , Отсюда: m_j ≤ ≤ f (ξ_j) ≤ M_j , . Почленно сложив эти неравенства, получим неравенства для интегральных сумм, которые требовалось доказать. ◄

2. τ) = τ) - τ) ; τ) = τ) - τ).

► Имеем (см. п.1.3, свойство 5): на промежутке Отсюда: и , Складывая эти равенства почленно, получим равенства для интегральных сумм. ◄

3. Всякая нижняя интегральная сумма функции f не превышает любой из её верх- них интегральных сумм, т.е. для любых двух дроблений τ′ и τ″ промежутка X = справедливо τ′) ≤ τ″).

► Пусть сначала f неотрицательна на X. Из включений (3) имеем для любых двух дроблений τ′ и τ″: и ; значит, .

Отсюда: ( ) ≤ ( ) , т.е. τ′) ≤ τ″).

Пусть теперь f – произвольная ограниченная на X функция, а и - её составляющие. Так как и неотрицательны, то по доказанному выше τ′) ≤ ≤ τ″) ; τ′) ≤ τ″). Отсюда и из равенств 2. следует:

τ′) = τ′) - τ′) ≤ τ″) - τ′) = τ″). ◄

Замечание. Обозначим через совокупность нижних интегральных сумм функ- ции f по всевозможным дроблениям промежутка . Из свойства 3. следует, что всякая верхняя интегральная сумма является верхней гранью множества . Пусть . Так как точная верхняя грань множества есть наименьшая из его верхних граней,то при любом дроблении τ справедливо ≤ τ).

Обозначим через совокупность верхних интегральных сумм функции f по все- возможным дроблениям промежутка . При любом дроблении τ справедливо ≤ ≤ τ) (см. выше); значит, число является нижней гранью совокупности . Обоз- начим: . Так как - нижняя грань множества , а - его точная нижняя грань, то ,. Таким образом, для произвольного дробления τ промежутка справедливы неравенства

τ) ≤ ≤ τ). (4)

2.7. Интегрируемые функции

Пусть τ = - дробление промежутка X = , a < b, образованное набором точек . Наибольшую из длин промежутков , назовем рангом дробления τ и обозначим через λ_τ .

Пусть имеем некоторую последовательность { τ_k} дроблений промежутка X :

τ₁ = , τ₂ = , … , τ_k = , … . Дробление τ_k образовано набором точек , x = a< x <x < … <x <x =b, так что 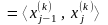. Последовательность { τ_k} назовем нормальной последова- тельностью дроблений, если последовательность {λ } их рангов является бесконечно малой : λ . Примером нормальной последовательности дроблений является последо- вательность {τ_k} , где дробление τ_k образовано набором точек, делящих на k равных частей.

Пусть функция f ограничена на промежутке , a < b.

Определение. Функцию f назовем интегрируемой на промежутке , если для любой нормальной последовательности { τ_k} дроблений этого промежутка разность между верхней и нижней интегральными суммами функции f по дроблению τ_k стремится к нулю: τ_k) - τ_k) .

Приведем пример интегрируемой функции.

Теорема 1. Пусть , a < b, любой ограниченный промежуток, а функция f огра- ничена на и либо непрерывна на нем, либо имеет конечное количество точек разры- ва. Тогда f интегрируема на .

► Если функция f удовлетворяет указанным выше требованиям, то существует набор точек , t₀ = a< t₁ <t₂ < … <t_n-1 <t_n =b, такой, что f непрерывна на каждом из интервалов , Точки этого набора являются, вообще говоря, точками разрыва функции f ; если f непрерывна на , то набор можно составить из двух точек a и b. Выберем ε₀ > 0 настолько малым, чтобы ε₀ – окрестности точек t_i , i = 1,2, …, n, попарно не пересекались. Обозначим: , . Очевидно, множества Х и Y не пересекаются, а всякая точка промежутка принадле- жит либо Х, либо Y. Функция f непрерывна на сегменте ; по теореме Кан- тора ([1], стр. 65) найдется такое, что для любых х′ и х″, принадлежащих cегменту и удовлетворяющих условию | х″- х′| < справедливо неравенство |f(х″) – f(х′)| < ε₀ . Обозначим через δ наименьщее из чисел , ,…, _n, ; тогда для любых х′ и х″, принадлежащих множеству Y и удовлетворяющих условию | х″- х′| < δ справедли- во неравенство |f(х″) – f(х′)| < ε₀.

Пусть τ = - дробление промежутка , ранг λ_τ которого меньше δ . Со- вокупность промежутков разобьем на две группы. К группе I отнесем промежутки Х_j , содержащиеся в множестве Y, остальные составят группу П; промежутки второй груп- пы либо содержатся в множестве Х, либо имеют непустые пересечения и с Х, и с Y. Имеем:

τ) - τ) = + . Здесь в и собраны слагаемые суммы , которые соответствуют промежуткам группы I и группы П. Если Х_j принадлежит группе I, то он содержится в множестве Y, и так как длина его меньше δ , то для лю- бых х′ и х″, принадлежащих Х_j , справедливо |f(х″) – f(х′)| < ε_0.; поэтому . Отсюда:

≤ ε₀ ≤ ε₀ (b - a) . (5)

Оценим . Обозначим: . Ясно, что 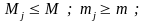значит, ≤ (M – m) . Оценим - сум- му длин промежутков Х_j, входящих в группу П. Всякий такой промежуток либо содержится в Х, либо имеет непустые пересечения как с Х, так и с Y. Множество Х состоит из n+1 по- парно не пересекающихся интервалов ; длина Х_j меньше δ ; значит, сумма длин всех промежутков из группы П не может превзойти величину 2 (n+1)( ε₀ + δ ), а это число меньше 4 ε₀ (n+ 1). Таким образом,

≤ (M – m) ≤ (M – m) 4 ε₀ (n+1). (6) Из (5) и (6) теперь получим:

τ) - τ) = + ≤ ε₀ (b - a) +

+(M – m) 4 ε₀ (n+1) = С ε₀ , (7) где С = (b - a) + 4 (M – m) (n+1) > 0 – константа, не зависящая от выбора ε₀ .

Пусть ε > 0 – заданное число, а { τ_k} - нормальная последовательность дроб- лений промежутка . Пусть ε₀ > 0 выбрано так, чтобы ε₀ – окрестности точек t_i , i = =1,2, …, n, попарно не пересекались и чтобы было выполнено условие ε₀ . По ε₀ найдем δ так, как было описано выше. Последовательность рангов {λ } стремится к нулю; значит, найдется натуральное такое, что при всех k > будет выполнено λ < < δ . В силу (7) при всех k > имеем: τ_k) - τ_k) ≤ С ε₀ < ε. Так как здесь ε > 0 любое, то отсюда следует: τ_k) - τ_k) . Здесь {τ_k} - произвольная нормаль- ная последовательность, значит, f удовлетворяет сформулированному выше определению. ◄

Следствие. Функция, непрерывная на сегменте, интегрируема на нем.

Действительно, функция непрерывная на сегменте, ограничена на нем (первая тео- рема Вейерштрасса); значит, она удовлетворяет всем требованиям теоремы 1.

Ниже в формулировках свойств интегрируемых функций - ограниченный промежуток, рассматриваемые функции интегрируемы на нём.

1. Сумма функций, интегрируемых на , интегрируема на .

► Пусть функции f и g интегрируемы на , а h = f + g . Рассмотрим дробление τ = промежутка . Тогда ( см. лемму, п. 1.2 ) при всех j = 1,2,…,l справедливы неравенства и . Отсюда: = = = .

Таким образом, при любом дроблении τ

Пусть - нормальная последовательность дроблений промежутка . При каждом натуральном k

0 ≤ . Так как функции f и g интегрируемы, обе скобки в правой части этого неравенства стре- мятся к нулю. Значит, , т.е. h интегрируема на . ◄

2. Пусть функция f ограничена на , а f и f - ее составляющие. Для того, чтобы f была интегрируемой на , необходимо и достаточно, чтобы на были интегрируемы f и f .

► Пусть τ = - некоторое дробление промежутка . В силу свойства 2., п.2.4,

=

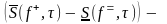
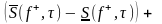
. Пусть - нормальная последовательность дроблений промежутка . Для каждо- го натурального k справедливо равенство

(8)

Необходимость. Пусть f интегрируема на . Тогда левая часть равенства (8) стремится к нулю при 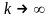. Обе скобки в его правой части неотрицательны; поэтому каждая из них стремится к нулю, т.е. f и f интегрируемы на .

Достаточность. Пусть f и f интегрируемы на . Тогда скобки в правой части равенства (8) стремятся к нулю при . Значит, , т.е. f интегрируема на . ◄

3. Если f интегрируема на , то функция g = | f | также интегрируема на .

► Так как f интегрируема, то интегрируемы f и f ; функция g = | f | = f + f интегрируема как сумма интегрируемых функций. ◄

4. Произведение функций, интегрируемых на , интегрируемо на .

► Пусть h = f g . Рассмотрим дробление τ = . Применив утверждение г) леммы из п. 1.2 к промежутку , можем записать :

.

Это неравенство справедливо при всех j = 1,2, …,l. Умножая обе его части на и по- членно складывая неравенства при j = 1,2, …,l, получим для произвольного дробления τ:

Пусть - нормальная последовательность дроблений промежутка . При каждом натуральном k

Так как f и g интегрируемые функции, обе скобки в правой части равенства стремятся к нулю при . Значит, 0, т.е. h - интегрируемая функция. ◄

Замечание. Произведение интегрируемой функции на число есть интегрируемая функция.

► Пусть функция f интегрируема на промежутке , а λ – заданное число. Зададим на функцию g: g(х) ≡ λ . Очевидно, эта функция интегрируема на . Значит, произведение f g , т.е. функция h = λf интегрируема на . ◄

5. Пусть a < c < b. Если функция f интегрируема на , то она интегрируема на и на

► Пусть - некоторое дробление промежутка , а - некоторое дробление промежутка . Совокупность, состоящая из всех промежутков и всех промежутков , представляет собой дробление промежутка ; обозначим его через , где . Будем говорить, что дробление τ есть обьединение дроблений и и записывать при этом: τ = . Заметим: если τ = ,то = + + ; аналогичное равенство справедливо и для верхних интегральных сумм. Отсюда :

= ( ) + ( ) (9)

Пусть и - нормальные последовательности дроблений промежут- ков и соответственно, и пусть при всех натуральных k τ_k = . Очевидно, есть нормальная последовательность дроблений промежутка . Из (9) получаем для всякого натурального k :

=( ) - ( ). (10)

Так как функция f интегрируема на промежутке , а - нормальная пос- ледовательность дроблений, то ; обе разности интегральных сумм в скобках в правой части (10) неотрицательны, значит, каждая из этих разностей стремится к нулю: и . Здесь и - произвольные нормальные последовательности дроблений промежутков и соответственно; следовательно, f интегрируема на и на ._. ◄

Замечание. Можно доказать справедливость обратного утверждения: если f интег- рируема на и на , то она интегрируема на .

6) Площадь графика интегрируемой функции равна нулю.

► Пусть функция f интегрируема на промежутке . а - некоторое дробление этого промежутка, образованное на- бором точек . Обозначим через С_j прямо- угольник, ограниченный п рямыми x=x_j-1 , x= x_j,, y= m_j , y = M_j , а через С(τ) – многоугольную фигуру, обьединение прямоугольников С_j , j = = 1, 2, …, l (рис. 5 ). График γ функции f со- держится в фигуре F(τ) , площадь которой равна , значит, для любого дробления справедливы неравенства .

Пусть есть нормальная последовательность дроблений промежутка . При всех натуральных k имеем: . Но 0 ; следовательно, ◄