
- •Методичка
- •§1. Неопределённый интеграл
- •§2. Определенный интеграл
- •§3. Несобственные интегралы
- •Несобственный интеграл по (a,b) ……………………………………… 44
- •§1. Неопределённый интеграл
- •1. 1. Первообразная функция
- •1.2. Неопределённый интеграл
- •1.4. Метод подстановки
- •1.5. Интегрирование рациональных функций
- •1.6. Интегрирование тригонометрических функций
- •1.7. Интегрирование дифференциального бинома
- •§ 2. Определенный интеграл
- •2.1. Площадь плоской фигуры
- •Площадь пустого множества λ равна нулю. Заметим, что площадь непустого мно- жества может равняться нулю.
- •2.2. Точные грани ограниченной функции
- •2.3. Положительная и отрицательная части функции
- •Интегральные суммы
- •2.6. Свойства интегральных сумм
- •2.7. Интегрируемые функции
- •2.8. Определенный интеграл
- •2.9. Свойства определенного интеграла, выражаемые равенствами
- •2.10. Свойства определенного интеграла, выражаемые неравенствами
- •2.11 Теоремы о среднем для определенного интеграла
- •2.12. Определенный интеграл с переменным верхним пределом
- •2.13. Способы вычисления определенных интегралов
- •§ 3. Несобственные интегралы
- •3.1. Несобственный интеграл по [a,b)
- •Замена переменной под знаком несобственного интеграла
- •3.6. Несобственный интеграл от функции, имеющей особые точки
§ 2. Определенный интеграл
2.1. Площадь плоской фигуры
В этом пункте термин “плоская фигура” или“фигура” означает некоторое множе- ство точек плоскости. Плоскую фигуру называют ограниченной, если можно указать по- ложительное число М такое, что расстояние между любыми двумя точками фигуры не превышает М. Ниже все фигуры предполагаются ограниченными. Две фигуры называют конгруентными, если существует движение плоскости (т.е. взаимно однозначное отобра- жение плоскости на себя, не меняющее расстояний между точками), при котором одна из фигур отображается на другую.
Площадь
фигуры F
обозначаем
через
 .
Напомним основные свойства ( акси- омы)
площади.
.
Напомним основные свойства ( акси- омы)
площади.
Аксиома 1. (Неотрицательность площади ) Площадь фигуры есть неотрицатель- ное число.
Аксиома 2. (Аддитивность площади) Площадь обьединения двух непересекаю- щихся фигур равна сумме их площадей.
Аксиома 3. (Инвариантность площади) Площади конгруентных фигур одинако- вы.
Аксиома 4. (Нормированность площади) Площадь единичного квадрата,т.е. квад- рата, длина стороны которого равна единице, равна единице.
Теоремы 1 и 2 о свойствах площади являются следствиями аксиом.
Теорема 1. (Монотонность площади) Если фигура F1 содержится в фигуре F2 , то площадь F1 не превышает площади F2.
► Обозначим:
 .
Так как
.
Так как
 ,
то
,
то
 ,
причем
,
причем
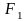 и
и
 не пересекаются. В силу аксиомы 2. имеем:
σ(F2)
= σ(F1)
+ σ(F)
. По
аксиоме 1 σ(F)
не пересекаются. В силу аксиомы 2. имеем:
σ(F2)
= σ(F1)
+ σ(F)
. По
аксиоме 1 σ(F) ;
значит,
σ(F2)
;
значит,
σ(F2)
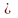 σ(F1).
◄
σ(F1).
◄
Площадь пустого множества λ равна нулю. Заметим, что площадь непустого мно- жества может равняться нулю.
Пример
1. Площадь
ограниченного отрезка прямой равна
нулю. Действительно, пусть F – прямолинейный
от- резок длины l
, а ε
– некоторое
положительное число. Обо- значим через
П ε
прямоугольник с измерениями
l
и
– прямолинейный
от- резок длины l
, а ε
– некоторое
положительное число. Обо- значим через
П ε
прямоугольник с измерениями
l
и
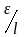 ,
содержащий отрезок F
( Рис. 1). Так
как
,
содержащий отрезок F
( Рис. 1). Так
как
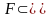 П ε ,то
σ(F)
≤ ≤ σ(П
ε
), т.е. 0 ≤
σ(F)
≤ ε. Но здесь
ε – любое
положительное число; значит, σ(F)
= 0.
П ε ,то
σ(F)
≤ ≤ σ(П
ε
), т.е. 0 ≤
σ(F)
≤ ε. Но здесь
ε – любое
положительное число; значит, σ(F)
= 0.
Теорема 2. ( Субаддитивность площади) 1) Площадь обьединения двух фигур не превышает суммы их площадей. 2) Если площадь пересечения двух фигур равна нулю, то площадь их обьединения равна сумме площадей этих фигур.
► Обозначим:
.
Имеем (рис.2 ):
 ,
причём
,
причём В силу аксиомы 2.
В силу аксиомы 2.
 =
σ(F1)
+ σ(F)
.
=
σ(F1)
+ σ(F)
.
1)
Так
как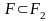 ,
то
σ(F)
≤ σ(F2);
значит,
,
то
σ(F)
≤ σ(F2);
значит,
σ(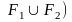 =
σ(F1)
+ σ(F)
≤
σ(F1)
+ σ(F2)
.
=
σ(F1)
+ σ(F)
≤
σ(F1)
+ σ(F2)
.
2)
Пусть 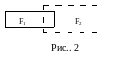
 .
Заметим:
.
Заметим:
 ,
при- чём
,
при- чём
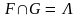 .
В силу аксиомы 2 σ(
.
В силу аксиомы 2 σ( =
σ(F)
+ σ(
=
σ(F)
+ σ(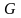 )
. Отсюда:
σ(F)=
σ(
-
σ(
)
. Но σ(
)=
0; значит,
σ(F)=
= σ(
.
Теперь получим:
)
. Отсюда:
σ(F)=
σ(
-
σ(
)
. Но σ(
)=
0; значит,
σ(F)=
= σ(
.
Теперь получим:
σ( = σ(F1) + σ(F) = σ(F1) + σ( . ◄
Замечание.
Таким образом,
равенство σ(
=
σ(F1)
+ σ(
имеет место не только в случае
непересекающихся фигур F1
и
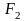 ,
оно справедливо и тогда, когда F1
и
пересекаются, но площадь их пересечения
равна нулю.
,
оно справедливо и тогда, когда F1
и
пересекаются, но площадь их пересечения
равна нулю.
2.2. Точные грани ограниченной функции
Здесь мы рассматриваем функции, определеные на некотором множестве Х веще- ственных чисел. Функцию f называют ограниченной на множестве Х, если ограничено множество значений, принимаемых этой функцией на Х.
Пусть f
– функция, ограниченная на
множестве Х ,
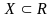 .
Введём обозначения точной нижней и
точной верхней граней множества её
значений:
.
Введём обозначения точной нижней и
точной верхней граней множества её
значений:
 .
.
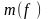 и
и
 называют соответственно точной нижней
и точной верхней гранями функции f
на множестве Х .
называют соответственно точной нижней
и точной верхней гранями функции f
на множестве Х .
Лемма. Пусть функции f и g ограничены на множестве Х. Тогда:
а) если
g = -f , то
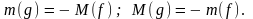 ;
;
б)
число -
-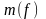 есть
точная верхняя грань множества значений
модуля разности
есть
точная верхняя грань множества значений
модуля разности
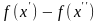 ,
где
,
где
 и
и
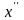 -
любая пара точек, принадлежащих Х :
-
любая пара точек, принадлежащих Х :
-
=
 ;
;
в) пусть h = f + g; тогда
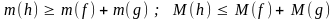 ;
;
г) пусть h = f ∙ g; тогда
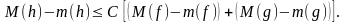 ,
,
где С – число такое, что
на множестве Х | |
≤ C и |
|
≤ C и |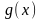 |
≤ C.
|
≤ C.
► а). Докажем
первое равенство. Для всякой точки
х справедливо
≤
≤
.
Отсюда, т.к. f = - g , получим
справедливо
≤
≤
.
Отсюда, т.к. f = - g , получим
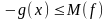 и
и
 ;
следовательно, число
;
следовательно, число
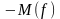 является нижней гранью множества
значений функции g. Точная нижняя
грань множества есть наибольшая из его
нижних граней; поэтому
является нижней гранью множества
значений функции g. Точная нижняя
грань множества есть наибольшая из его
нижних граней; поэтому
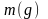
 .
С дру- гой стороны, для всякой точки
х
справедливо
.
С дру- гой стороны, для всякой точки
х
справедливо
 ;
отсюда получим
;
отсюда получим
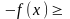 ≥
≥ и
и
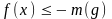 .
Следовательно,
.
Следовательно,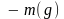 есть верхняя грань множества значений
функции f , а
есть верхняя грань множества значений
функции f , а
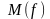 есть наименьшая из его верхних граней;
поэтому
есть наименьшая из его верхних граней;
поэтому
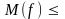
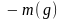 .
Таким образом, с одной стороны
,
а с другой
;
значит,
=
.
Таким образом, с одной стороны
,
а с другой
;
значит,
= .
Доказательство равенства
.
Доказательство равенства

 аналогично.
аналогично.
б) Обозначим
через Е ножество значений разности
,
где
и
-
лю- бая пара точек, принадлежащих Х.
Обозначим : А =
-
.
Докажем: А= sup Е
. Равенство А = sup
Е
означает, во-первых, что А есть
верхняя грань множества Е
, т.е.
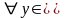 Е
Е
 и, во- вторых, что при любом ε
> 0 число А - ε
верхней гранью множе – ства Е не
является, т.е.
и, во- вторых, что при любом ε
> 0 число А - ε
верхней гранью множе – ства Е не
является, т.е.

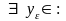 Е:
Е: .
Убедимся, что число А этими свойствами
обладает.
.
Убедимся, что число А этими свойствами
обладает.
1) При любых
и
,
принадлежащих Х, имеем:
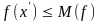 ,
,
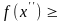
 ;
отсюда:
≤
-
=
А, Значит, А есть верхняя грань
множества Е
.
;
отсюда:
≤
-
=
А, Значит, А есть верхняя грань
множества Е
.
2) Пусть задано
ε > 0. Так как
и
-
точные грани множества значений функции
f , в Х существуют
точки
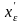 и
и
 такие, что справедливы неравенства
f(
)>
такие, что справедливы неравенства
f(
)>
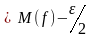 и f(
)
и f(
)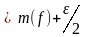 .
Обозначим:
.
Обозначим:

 .
Очевидно,
.
Очевидно,

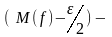
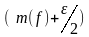 =
=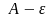 .
Таким образом, для всякого ε
> 0 можно указать принадлежащее Е
число
-
такое, что
.
Таким образом, для всякого ε
> 0 можно указать принадлежащее Е
число
-
такое, что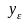 >
;
эначит, при всяком ε
> 0 число
верхней гранью мно- жества Е
не является. Из 1) и 2) следует:
А – наименьшая из верхних граней
множества Е
, т.е.
>
;
эначит, при всяком ε
> 0 число
верхней гранью мно- жества Е
не является. Из 1) и 2) следует:
А – наименьшая из верхних граней
множества Е
, т.е.
 .
.
Очевидно, множество Е симметрично относительно точки 0, поэтому sup Е =
=
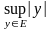 .
Отсюда:
=
А =
-
.
Отсюда:
=
А =
-
в) Для
всякой точки х
,
очевидно, справедливо

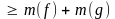 .
Следовательно,
.
Следовательно, является нижней гранью множества значе-
является нижней гранью множества значе-
ний функции h;
поэтому


 ,
так как
,
так как
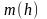 -
наибольшая из нижних граней. Доказательство
второго неравенства аналогично
-
наибольшая из нижних граней. Доказательство
второго неравенства аналогично
.г) Функции
f и g
ограничены на множестве Х; значит,
найдётся С> 0, такое, что для любой
точки
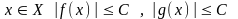 Пусть
и
-
точки, принадлежащие Х. Легко
убедиться, что
Пусть
и
-
точки, принадлежащие Х. Легко
убедиться, что



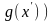 .
Отсюда: для любых
и
,
принадлежащих Х ,
.
Отсюда: для любых
и
,
принадлежащих Х ,
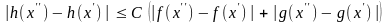 .
Тогда подавно
справедливо неравенство
.
Тогда подавно
справедливо неравенство
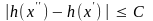 (
( +
+
 ). В силу утверждения
б) леммы это неравенство можно
записать так:
). В силу утверждения
б) леммы это неравенство можно
записать так:
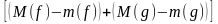
Таким образом,
число С
есть верхняя грань множества значений
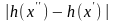 ;
поэтому
;
поэтому

 .
В силу утверждения б) леммы левая
часть этого неравенства равна
.
В силу утверждения б) леммы левая
часть этого неравенства равна
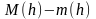 .
◄
.
◄
