1.4. Метод подстановки
Пусть функция определена на промежутке Х, а функция (t) определена на промежутке Т и удовлетворяет следующим требованиям:
1)
Множество значений
на Т
есть промежуток X;
2) дифференцируема на Т;
3)
либо
,
либо
.
Тогда
функция
строго монотонна на Т,
а обратная функция
строго
мо- нотонна и дифференцируема на X,
причём
( см. глава 2, п.п. 1.3 и 3.1).
Пусть
есть
первообразная на Т
для
функции
:
.
Обозначим:
,
где
.
Заметим:
(напомним:
так как
,
то
).
Таким образом,
если удалось отыскать первообразную
функции
,
то можно найти первообразную
функции
:
.
Пусть
требуется отыскать
.
Допустим, что удалось подобрать функцию
,
удовлетворяющую на Т
требованиям 1), 2) , 3) (см. выше), и такую,
что известен способ вычисления интеграла
:
íà
.
Тогда функция есть первообразная для , значит,
на
X.
Изложенное
решение задачи об отыскании
записывают в виде цепочки равенств:
.
Однако, следует указать на условность
написанных равенств. Так, интегралы
и
,
вообще говоря, не равны друг другу. Они
не равны хотя бы уже потому, что функции
множества
(первообразные
для
)
определены на Х,
а
функции второго множества
определены на промежутке Т,
который может не совпадать с Х.
Указан- ные равенства представляют
собой всего лишь удобную форму записи
выкладок, которые приводят к верному
равенству
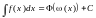на X.
Говорят,
что равенство
есть
результат замены в интегра- ле
"старой" переменной интегрирования
х
на
"новую" переменную интегриро- вания
t,
связанную с х
формулой (подстановкой)
.
Равенство
получено заменой t
на х
с
помощью обратной подстановки
.
Пример 5. Вычислим (см. также пример 4 )
Подынтегральная
функция определена на интервале X=
.
Положим
.
Множество значений этой функции на
интервале
.есть
интервал Х,
она дифференцируема на Т,
причём
на Т.
Таким образом,
удовлетворяет на Т
требованиям
1), 2) , 3), указанным в начале этого пункта.
В за- данном интеграле заменим переменную
х
на
переменную t
:
.
Получим:
.
Подстановка оказалась удачной:
интеграл
вычислен, найдена перво- образная
.
Возвратимся к "старой" переменной,
для чего уравнение
разрешим относительно t:
.
Получим:
.
Преобразуем правую
часть этого равенства:
.
Теперь окончательно
получим:
на
.
1.5. Интегрирование рациональных функций
В
самом общем случае рациональная функция
R(x)
– это рациональная дробь, т.е., отношение
двух алгебраических многочленов.
Рассмотрим сначала интегралы от простых
рациональных дробей, т.е., дробей вида
и
,
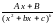где
,
b,
c,
A,
B
–вещественные числа, причём
,
k
– натуральное число.
1.
.
1)
.
.
2)
.
.
11.
.
1)
,
.
Обозначим:
.
.
2)
,
.
Преобразуем подынтегральное выражение,
выделив в числителе производную от
.
.
3) .
Лемма.
Пусть a,
,
– некоторое число, k
– натуральное число. Обозначим:
.
При всяком k,
,
справедливо равенство:
.
(1)
К интегралу
применим формулу интегрирования "по
частям". Положим
.
Тогда
,
.
Получим:
.
Заметим:
=
Значит,
.
Из этого равенства вытекает формула (1).
Формула
(1) позволяет найти интеграл
для любого
,
.
Действительно, справедлива “табличная
” формула
.
Поло- жив в (1)
,
найдём
:
.
Зная интеграл
,
можно найти
,
для чего следует в (1) положить
:
.
Вычислив
,
можно найти
,
положив в (1)
,
и т.д.
Теперь
рассмотрим интеграл
при
.
Перейдём к "новой" переменной
интегрирования t,
положив
Получим (
):
.
Вычислив
с
помощью формулы (1), возвратимся к "старой"
переменной x,
положив
.
Пример
1.
Вычислим
.
Здесь
,
,
,
.
Заметим:
.
.
.
Положим
в (1)
,
:
.
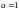Теперь получим:
.
Итак, первообразная любой простой рациональной дроби представляет собой элементарную функцию – она выражается через простые дроби, логарифмы и арктан- генсы.
Рациональную
дробь
называют
правильной, если степень многочлена в
чис- лителе меньше степени знаменателя:
.
Правильная дробь может быть разложена
в сумму простых дробей (см. глава
“Комплексные числа”, §2). Следовательно,
интеграл от правильной дроби можно
отыскать, представив подынтегральную
дробь в виде суммы простых дробей.
Пример.
Вычислить
.
Разложение подынтегральной дроби в сумму простых дробей получено в примере 1, §2 главы “Комплексные числа”:
.
Значит,
.
Имеем:
.
.
.
,
где
.
Этот интеграл найдем по формуле (1),
положив в ней k=1,
:
.
Итак,
.
Чтобы
проинтегрировать неправильную
рациональную дробь
,
,
следует, выделив её целую часть,
представить дробь в виде суммы целой
части (алгебра- ического многочлена) и
правильной рациональной дроби:
.
Интегрируя это равенство,
получим:
.
Таким образом, описанные выше действия обеспечивают, в принципе, возмож- ность проинтегрировать любую рациональную функцию R(x), причём интеграл будет выражен через элементарные функции – алгебраические многочлены, рациональные дроби, логарифмы, арктангенсы.
Один
из основных способов интегрирования
функций других типов состоит в применении
рационализующих подстановок, т.е.,
подстановок, с помощью которых ин- теграл
от
нерациональной функции
преобразуется в интеграл
от рациональной функции
R(x).
В последующих пунктах описаны некоторые
из таких под- становок.