Дослідити залежність величини валового регіонального продукту від величини витрат населення
Факторна ознака (x)- величина валового регіонального продукту
Результуюча ознака (y)-величина витрат населення
№ |
Регіон |
Валовий регіональний продукт у факт. цінах , млн. грн. X |
Витрати населення, млн. грн. Y |
|
п/п |
|
|||
1 |
АР Крим |
20874 |
25501 |
|
2 |
Вінницька |
15381 |
15865 |
|
3 |
Волинська |
10072 |
12428 |
|
4 |
Дніпропетровська |
71173 |
50141 |
|
5 |
Донецька |
92093 |
58974 |
|
6 |
Житомирська |
11127 |
12594 |
|
7 |
Закарпатська |
10508 |
11483 |
|
8 |
Запорізька |
33158 |
29284 |
|
9 |
Івано-Франківська |
13916 |
13043 |
|
10 |
Київська |
26221 |
20686 |
|
11 |
Кіровоградська |
9989 |
10271 |
|
12 |
Луганська |
32280 |
25741 |
|
13 |
Львівська |
27987 |
33649 |
|
14 |
Миколаївська |
14767 |
13380 |
|
15 |
Одеська |
33116 |
34494 |
|
16 |
Полтавська |
28355 |
18242 |
|
17 |
Рівненська |
11180 |
11983 |
|
18 |
Сумська |
12341 |
12179 |
|
19 |
Тернопільська |
8276 |
10304 |
|
20 |
Харківська |
43868 |
45645 |
|
21 |
Херсонська |
9034 |
12480 |
|
22 |
Хмельницька |
12339 |
13497 |
|
23 |
Черкаська |
13656 |
14684 |
|
24 |
Чернівецька |
6672 |
8104 |
|
25 |
Чернігівська |
11532 |
12143 |
|
1. Побудова аналітичного групування
Аналітичне групування – це статистична таблиця в якій вказані інтервали значень факторної ознаки, згідно з якими згруповані одиниці сукупності, а також наведені групові середні значення результуючої змінної.
Кількість груп аналітичного групування встановимо за формулою Стерджеса:
k=1+3,322Lg25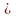
6
Розмір інтервалу:
,
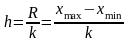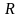- розмір сукупності,
,
-
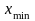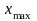відповідно найменше і найбільше значення
факторної ознаки.
=6672, =92093
h=(92093-6672)\6=14237
побудуємо аналітичне групування:
№ |
Валовий регіональний продукт у факт. цінах , млн. грн. |
Кількість регіонів |
Витрати населення, млн. грн. |
||
1 |
6672-20909 |
16 |
13121,19 |
||
|
|||||
2 |
20909-35146 |
6 |
27016 |
||
3 |
35146-49383 |
1 |
45645 |
||
4 |
49383-63620 |
0 |
0 |
||
5 |
63620-77857 |
1 |
50141 |
||
6 |
77857-92094 |
1 |
58974 |
||
Разом |
25 |
|
|||
У середньому |
32482,865 |
||||
Результати аналітичного групування можна подати у графічному вигляді. Для цього у декартовій системі координат по осі абсцис відкладають середини інтервалів значень факторної ознаки, а по осі ординат групові середні значення результуючої змінної. Отримана ламана лінія називається емпіричною лінією регресії.
2.Побудова парної лінійної кореляційно-регресійної моделі.
Будемо вважати, що кореляційна залежність результуючої змінної від факторної ознаки є лінійною і описується рівнянням регресії (узагальнена ПЛКРМ):
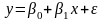
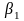- коефіцієнт
регресії,
-
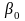вільний член регресії.
-
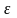випадкова величина, яка містить
різноманітні стохастичні збурення,
помилки спостереження та вимірювання
тощо. Вона не спостерігається
Оскільки ці
параметри нам невідомі, то ми повинні
здійснити їх оцінку. Щоб одержати оцінки
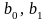параметрів
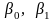на основі заданих статистичних даних
необхідно побудувати рівняння регресії
(вибіркову ПЛКРМ) :
-
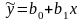
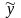теоретичне, нормативне або прогнозне
значення результуючої змінної.
Емпіричні дані,
на підставі яких будують модель це
вибірка значень
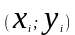двовимірного випадкового вектора (X;Y).
Вважатимемо, що параметри
моделі для кожного спостереження
залишаються постійними, а змінна епсілон
набуває різних значень, проте її неможливо
спостерігати.
Щоб одержати оцінки застосуємо метод найменших квадратів, знайшовши мінімум функції:
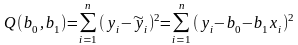
Тобто знаходимо
такі значення параметрів
, при яких значення суми квадратів
відхилень заданих значень результуючих
змінних
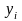від відповідних їм нормативних значень
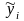найменше. Щоб знайти
слід розв’язати систему:
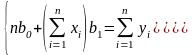
Скористаємося формулами для практичного розрахунку :
№ |
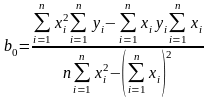
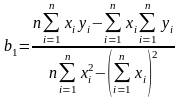
Валовий регіональний продукт у факт. цінах , млн. грн. |
Витрати населення, млн. грн. |
|
|
п/п |
|
|
||
|
xi |
yi |
xi*yi |
xi*xi |
1 |
20874 |
25501 |
532307874 |
435723876 |
2 |
15381 |
15865 |
244019565 |
236575161 |
3 |
10072 |
12428 |
125174816 |
101445184 |
4 |
71173 |
50141 |
3568685393 |
5065595929 |
5 |
92093 |
58974 |
5431092582 |
8481120649 |
6 |
11127 |
12594 |
140133438 |
123810129 |
7 |
10508 |
11483 |
120663364 |
110418064 |
8 |
33158 |
29284 |
970998872 |
1099452964 |
9 |
13916 |
13043 |
181506388 |
193655056 |
10 |
26221 |
20686 |
542407606 |
687540841 |
11 |
9989 |
10271 |
102597019 |
99780121 |
12 |
32280 |
25741 |
830919480 |
1041998400 |
13 |
27987 |
33649 |
941734563 |
783272169 |
14 |
14767 |
13380 |
197582460 |
218064289 |
15 |
33116 |
34494 |
1142303304 |
1096669456 |
16 |
28355 |
18242 |
517251910 |
804006025 |
17 |
11180 |
11983 |
133969940 |
124992400 |
18 |
12341 |
12179 |
150301039 |
152300281 |
19 |
8276 |
10304 |
85275904 |
68492176 |
20 |
43868 |
45645 |
2002354860 |
1924401424 |
21 |
9034 |
12480 |
112744320 |
81613156 |
22 |
12339 |
13497 |
166539483 |
152250921 |
23 |
13656 |
14684 |
200524704 |
186486336 |
24 |
6672 |
8104 |
54069888 |
44515584 |
25 |
11532 |
12143 |
140033076 |
132987024 |
сума |
579915 |
526795 |
18635191848 |
23447167615 |
Таблиця 3. Вихідні дані та допоміжні розрахунки для обчислення залежності витрат населення до валового регіонального продукту в фактичних цінах
За методом найменших квадратів маємо:
=
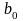6183
=
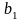0,6418
Рівняння регресії має вигляд:
=6183+0,64x
Областю існування кореляційно-регресійної моделі є інтервал
X [6672;92094]
Таблиця 4. Теоретичні значення
х |
|
|
20874 |
19542,36 |
|
15381 |
16026,84 |
|
10072 |
12629,08 |
|
71173 |
51733,72 |
|
92093 |
65122,52 |
|
11127 |
13304,28 |
|
10508 |
12908,12 |
|
33158 |
27404,12 |
|
13916 |
15089,24 |
|
26221 |
22964,44 |
|
9989 |
12575,96 |
|
32280 |
26842,2 |
|
27987 |
24094,68 |
|
14767 |
15633,88 |
|
33116 |
27377,24 |
|
28355 |
24330,2 |
|
11180 |
13338,2 |
|
12341 |
14081,24 |
|
8276 |
11479,64 |
|
43868 |
34258,52 |
|
9034 |
11964,76 |
|
12339 |
14079,96 |
|
13656 |
14922,84 |
|
6672 |
10453,08 |
|
11532 |
13563,48 |
