Питання для самоперевірки

1. Який рух називається поступальним ?

2. Що таке матеріальна точка ?

3. Дати визначення швидкості поступального руху тіла.

4. Дати визначення середній і миттєвій швидкостям тіла.

5. Що характеризує тангенціальне прискорення ? Як визначається його величина і напрямок ?

6. Що характеризує нормальне прискорення ? Як визначається його величина і напрямок ?

7. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення а_n = 0, а тангенціальне прискорення a_t > 0 ?

8. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення а_n = const, а тангенціальне прискорення a_t = 0 ?

9. Запишіть і сформулюйте основне рівняння динаміки матеріальної точки.

10. Запишіть і сформулюйте закон Стокса.

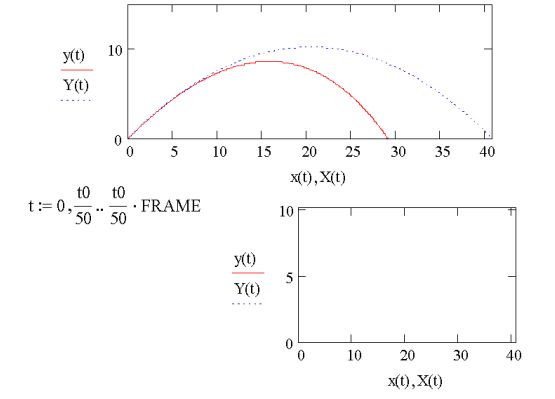
Додаток

MATHCAD-PROGRAM

g:=9.8 x0:=0 y0:=0 v0:=20 m:=0.5 r:=0.1

v0x:=v0cos() v0y:=v0sin()

Лабораторна робота № 2 Визначення моменту інерції системи на прикладі маятника Обербека

Мета роботи: експериментально визначити момент інерції системи динамічним методом та порівняти отримані результати з теоретичними обчисленнями.

Прилади та обладнання: маятник Обербека, міліметрова лінійка, секундомір.

Теоретичні відомості

Обертальним рухом твердого тіла (системи) відносно нерухомої осі називається такий рух, під час якого всі точки тіла (системи) рухаються в площинах, перпендикулярних до осі обертання, і описують кола з центрами на цій осі.

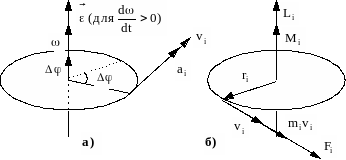
Рис. 1.

Кінематика та динаміка обертального руху характеризується відповідно кутом повороту , приростом кута повороту , кутовою швидкістю , кутовим прискоренням , моментом інерції J, моментом сили , моментом імпульсу , які виконують таку саму роль для обертального руху, як і відповідні величини – шлях S, переміщення , швидкість , прискорення та маса m, сила , імпульс - для поступального руху. Зв’язок між лінійними і відповідними кутовими кінематичними величинами здійснюється через радіус обертання r (радіус-вектор ) таким чином:

s = r, , , .

Динамічні характеристики обертального руху визначаються наступними виразами:

, ,

.

Взаємозв’язок між відповідними величинами додатково розкривається при графічному зображенні векторних величин, що розглядаються в лабораторній роботі (див. рис. 1: а – кінематика, б – динаміка).

Основний закон динаміки обертального руху тіла відносно нерухомої осі обертання має наступний вигляд:

. (1)

Для тіл правильної геометричної форми момент інерції простіше визначити аналітично, для тіл неправильної геометричної форми – експериментально. З експериментальних найбільш поширеними є методи, які основуються на використанні основного закону динаміки обертального руху, закону збереження та перетворення енергії та законів коливального руху.

Опис методу

Рис. 2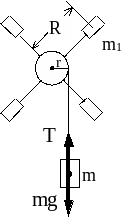

У роботі використовується динамічний метод із застосуванням основного закону динаміки обертального руху.

Маятник Обербека, момент інерції якого треба визначити, складається із закріпленого на горизонтальній осі шківа (рис. 2) з радіально розташованими стержнями, на яких симетрично закріплені чотири тягарці масами m₁. На шків намотана нитка, один кінець якої закріплений до шківа, а на другому кінці підвішений тягарець масою m. Під час опускання тягарця m маятник Обербека під дією сили натягу нитки приводиться в рівноприскорений обертальний рух.

Основне рівняння динаміки обертального руху для маятника Обербека має вигляд:

, (2)

де r– радіус шківа. Моментом сили тертя нехтуємо.

Напрямок вектора моменту вздовж осі обертання маятника визначається векторним добутком (за правилом свердлика):

.

Прирівнявши праві частини рівнянь (1) та (2), отримаємо

,

звідки: . (3)

Робочу формулу для розрахунку моменту інерції J знайдемо, використавши величини h і t, які вимірюються в процесі експерименту, де h – шлях руху тягарця m по вертикалі, t – час його руху.

Виразивши кутове прискорення  через лінійне прискорення точок a, які знаходяться на ободі шківа, зведемо задачу до знаходження лише a. Оскільки тягарець m рухається прямолінійно і рівноприскорено, то його шлях h, пройдений за час t, можна визначити за формулою:

, звідки .

Тоді кутове прискорення маятника: .

Підставивши значення a та  у рівняння (3), отримаємо:

. (4)

Якщо врахувати можливі числові значення величин в нашому експерименті (h  1 м, t  10 c  gt²/2h  500), то в формулі (4) можна знехтувати одиницею і отримати спрощений вираз: . (5)

Формула (5) є робочою для експериментального визначення моменту інерції маятника Обербека. В роботі виконуються прямі вимірювання величин h і t, значення величин m, m₁ та r наведені в паспорті установки.