МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТРАНСПОРТНИЙ УНІВЕРСИТЕТ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання лабораторних робіт

з використанням комп’ютерного експерименту

з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій”

в рамках кредитно–модульної системи

організації навчального процесу

ЗАТВЕРДЖЕНО

на засіданні навчально–методичної Ради

Національного транспортного університету

Протокол №___від______________2007 р.

Київ НТУ 2007

Методичні вказівки до виконання лабораторних робіт з використанням комп’ютерного експерименту з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій” в рамках кредитно–модульної системи організації навчального процесу // Укл.: Гололобов Ю.П., Іщенко Р.М., Шатній Т.Д. – К.: НТУ, 2007. – 37 с.

Укладачі: Гололобов Ю.П. – доктор фіз.-мат. наук

Іщенко Р.М. – кандидат фіз.-мат. наук

Шатній Т.Д. – кандидат фіз.-мат. наук

Відповідальний за випуск: Іщенко р.М. Вступ

На сучасному етапі розвитку суспільства бути кваліфікованим спеціалістом неможливо без знань основних концепцій сучасного природознавства. Формування наукового світогляду та наукового стилю мислення у значній мірі залежить від засвоєння найбільш важливих досягнень природознавства як сукупності наук про природу. Кожен студент, який в подальшому збирається стати менеджером, економістом чи юристом, щоб почувати себе високоосвіченою людиною, повинен знати що таке теорія відносності, квантова механіка, синергетика та інші науки.

Навчальною програмою з дисципліни „Концепції сучасного природознавства” окрім лекційного курсу передбачено виконання студентами циклу лабораторних робіт. Такий підхід сприяє формуванню навичок щодо використання одержаних знань для розв’язку практичних задач, зокрема техніко-інженерного напрямку. Кредитно–модульна система організації навчального процесу, яка впроваджується в Національному транспортному університеті, передбачає використання як традиційних методів виконання лабораторних робіт (проведення фізичного експерименту), так і новітніх методів, зокрема, використання комп’ютерного експерименту. Тому в даних методичних вказівках до виконання лабораторних робіт з дисципліни „Концепції сучасного природознавства” для студентів спеціальності „Менеджмент організацій” разом з роботами, які виконуються безпосередньо при проведені фізичного експерименту, представлено лабораторну роботу „Моделювання криволінійного руху тіла”, що виконується з використанням комп’ютерного експерименту. Для покращення засвоєння навчального матеріалу в методичних вказівках після кожної лабораторної роботи наведено питання для самоперевірки знань студентів.

Лабораторна робота № 1 (з використанням комп’ютерного експерименту) Моделювання криволінійного руху тіла

Мета роботи: вивчити основні положення кінематики і динаміки матеріальної точки та закономірності руху тіл в однорідному полі тяжіння. Дослідити вплив опору повітря на форму траєкторії, дальність і висоту польоту.

Теоретичні відомості

Нехай тіло масою m кинуто під кутом α до горизонту зі швидкістю v₀. Знайдемо його траєкторію з врахуванням опору повітря і порівняємо її з траєкторію, отриманою при нехтуванні опором повітря.

Вважаючи тіло матеріальною точкою, запишемо для нього другий закон Ньютона:

, (1)

де g  прискорення вільного падіння, v = v(t)  швидкість тіла у довільній момент часу t,  cила опору повітря. Згідно з законом Стокса:

, (2)

де r – коефіцієнт опору (він залежить від розмірів і форми тіла та від властивостей середовища, в якому тіло рухається).

Виберемо декартову систему координат так, щоб вектор початкової швидкості знаходився у площині Oxy, спрямуємо вісь Oy вертикально вгору перпендикулярно поверхні землі і позначимо через координати тіла у довільний момент часу t. У проекціях на координатні вісі другий закон Ньютона (рівняння руху) набуває вигляду:

, (3а)

(3b)

або

, (4а)

. (4b)

Якщо у момент кидання t = 0 тіло знаходиться у точці з координатами х₀, у₀, то початкові умови задачі є такими:

при t = 0 x = x₀, y = y₀, , , (5)

де , (6)

– проекції початкової швидкості на вісі координат.

Розв’яжемо отримані диференціальні рівняння для двох випадків.

1. Опором повітря нехтуємо, r = 0. Запишемо для цього випадку рівняння (3а, 3b):

,

та інтегруємо їх з врахуванням початкових умов (5):

В результаті отримуємо відомі формули:

v_x = v_0x, v_y = v_0y – gt, (7)

згідно з якими рух тіла у горизонтальному напрямку є рівномірним, а у вертикальному – рівноприскореним.

Знайдемо траєкторію тіла у параметричному вигляді : х = х (t),

у = у (t). Для цього врахуємо, що v_x = dx/dt, v_y = dy/dt, перепишемо рівняння (7) у вигляді:

dx = v_0x·dt, dу = v_0y·dt – gt·dt

і проінтегруємо їх з врахуванням початкових умов (5):

,

.

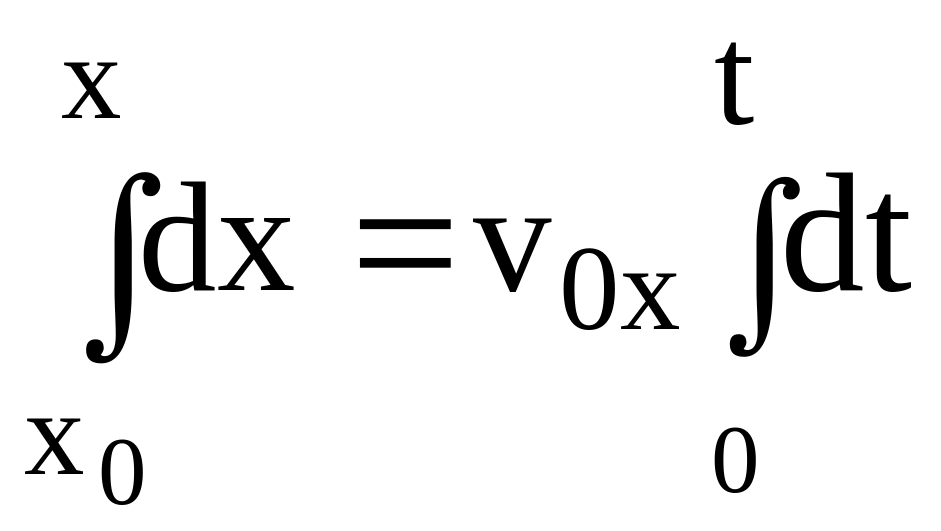В результаті отримуємо траєкторію тіла:

x(t) = x₀ + v_0xt, (8a)

y(t) = y₀ + v_0yt – gt² . (8b)

2. Враховуємо силу опору повітря, r > 0. У цьому випадку інтегруємо рівняння (4а):

і знаходимо:

(9)

де β = r/m. (10)

Аналогічно, інтегруючи рівняння (4b):

знаходимо:

(11)

Зауважимо, що при формули (9) і (11) переходять у формули (7).

Для знаходження траєкторії тіла у параметричному вигляді інтегруємо з врахуванням початкових умов (5) рівняння (9) і (11):

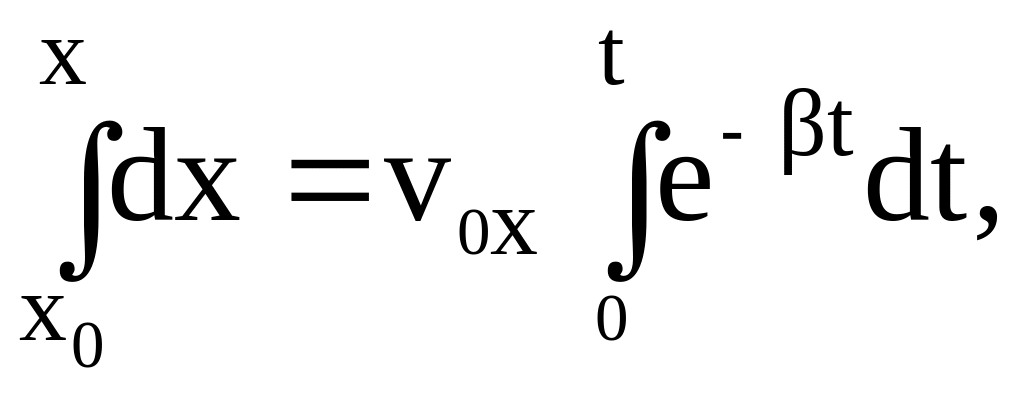
В результаті знаходимо траєкторію тіла з врахуванням сили опору повітря:

, (12a)

(12b)